تابع زتا (ریاضی ها ببیند)

seyed iman · 1390/10/4

تعریف تابع زتا ریمان:
حالا میخوایم زتای 2 رو بدست بیاریم.چند تا راه داره من میخوام راه کلی برای زتای 2n رو بگم ولی اول شما راهتون رو بگین.

goodarz · 1390/10/4

پاسخ : تابع زتا (ریاضی ها ببیند)

اثباتی که میخواید بکنید با استفاده از اعداد برنولیه؟ یعنی این:

؟ من خیلی دوست دارم این اثباتو ببینم :3:

goodarz · 1390/10/4

پاسخ : تابع زتا (ریاضی ها ببیند)

یه سری اثبات (به جز اون برنولی) هم اینجا هست: Basel problem - Wikipedia, the free encyclopedia

seyed iman · 1390/10/7

پاسخ : تابع زتا (ریاضی ها ببیند)

من اثباتم نیمه کارست تقریبن.
من فیزیکیم ما به اثبات "گیر" نمیدیم ولی خیلی خیلی جالبه.یعنی به یه رابطه ازگشتی رسیدم که فکر کنم به اون برنولیه برسم.
سعی میکنم به زودی بزارمش.این هم خییلی جالب بود.اویلر واقعن خفن بوده و عجیبه که برنولیها اینو حل نکردن!!!
منم با سری فوریه حل کردم.منتها برای 2n

amir.ekhlasi · 1390/10/7

پاسخ : تابع زتا (ریاضی ها ببیند)

اون اثباتی که من بلدم خیلی سخته و از روابط آنالیز مختلط استفاده میکنه. ولی خوب الان به روابطی که از روی هم به دست می آیند و با اونا،میشه اینا ثابت کرد اشاره میکنم (هر جا z به کار بردم یعنی اعداد مختلط و هرجا n به کار بردم، یعنی اعداد طبیعی):
روالط تابع گاما:

$\Gamma (z+1)=z\Gamma (z)$

$\Gamma(z)\Gamma(1-z)=\frac{\pi}{\sin \pi z}$

رابطه برنولی:

$\frac{z}{e^z-1}=1+\sum _{n=1}^\infty {\frac{B_nz^n}{n!}}$

روابط تابع یوتا:

$I(z)=\int_\gamma {(e^w-1)^{-1}(-w)^z\frac{dw}{w}}$

که در آن

$\gamma$

یک منهنی خاصی است که اگر خواستید توضیح میدم.

$I(-n)=2\pi i (-1)^n \frac{B_{n+1}}{(n+1)!}$

$I(z)=2i\sin (\pi z)\int_0^\infty{\frac{t^{z-1}}{e^t-1}dt}$

روابط تابع زتا :

$\zeta(z)=\frac{\Gamma(1-z)}{2\pi i}I(z)$

$\zeta(z)=2(2\pi)^{z-1}\sin(\frac{\pi z}{2})\Gamma(1-z)\zeta(1-z)$

$\zeta(-n)=(-1)^n\frac{B_{n+1}}{n+1}$

amir.ekhlasi · 1390/10/7

پاسخ : تابع زتا (ریاضی ها ببیند)

تعجب نکنید. این پروژه پارسالم بوده.

Mahdi73 · 1390/10/7

پاسخ : تابع زتا (ریاضی ها ببیند)

یکی بیاد تعریف این تابع رو بگه

goodarz · 1390/10/7

پاسخ : تابع زتا (ریاضی ها ببیند)

Riemann zeta function - Wikipedia, the free encyclopedia

Mahdi73 · 1390/10/7

پاسخ : تابع زتا (ریاضی ها ببیند)

خیلی ممنون

seyed iman · 1390/10/7

پاسخ : تابع زتا (ریاضی ها ببیند)

اخلاصی دمت گرم.ترکوندی سوال رو!!!:212::212:
رابطه دومی گاما که با تعریف وایراشتراوس از گاما در می آد.و همینطوور رابطه اولش بدیهیه.
از اون جا به بعد رو نمی فهمم.اون یوتا چیه؟منحنی گاما چیه؟منحنی رو یه جوری تعریف کردی که لم جردن بزنی بتونی انتگرال با قضیه کوشی بگیری؟
رابطه های زتا رو از کجا آوردی؟
من فقط اومدم سری فوریه ی x بتوان 2n رو نوشتم و یک رابطه بازگشتی برای زتا بدست آوردم که زتا های زوج از توش در میآد.
مثه کاری که آرفکن برای بدست آوردن زتای 2 کرده(تو لینک گودرز هم هست).منتها برای 2n.

amir.ekhlasi · 1390/10/7

پاسخ : تابع زتا (ریاضی ها ببیند)

مرحله به مرحله هر وقت حال کردم توضیح میدهم.
برای رابطه سوم، اگر طرفین، وسطین کنید و بعد بسط

$e^z=\sum \frac{z^n}{n!}$

را بنویسید طبق رابطه بازگشتی برنولی درمیاد.
با رابطه چهارم تابع یوتا را تعریف کردم. ولی در مورد منحنی گاما حرفت درسته. یه جوری تعریف کردم که بعدا بتونم روش قضیه کوشی بزنم. چون حال توضیح دادنش را ندارم، عکسش را میذارم: http://s2.picofile.com/file/7227659779/Untitled.png . درواقع منحنی از بینهایت (بالای محور x ها) تا نزدیکی 0 مستقیم میآید، بعد یک دایره به شعاع نزدیک صفر میزند که قسمتی از کمانش حذف میشود و بعد، دوباره از زیر محور x ها به سمت بینهایت میرود. زاویه بردارها هم برای تابع log از

$-\pi$

تا

$\pi$

متغیر است. (که در واقع برای قسمت مثبت محور x ها در حالت حدی هر دو عدد است.)
بقیه روابط را در پستهای بعد توضیح میدم. الان دیروقته.

amir.ekhlasi · 1390/10/8

پاسخ : تابع زتا (ریاضی ها ببیند)

قبل از اینکه ادامه بدم به باید به چند نکته مهم تو آنالیز مختلط اشاره کنم. اون برای اینه که تو اثباتا ازش استفاده میکنم. ولی پیشنهاد میکنم آنالیز مختلط را بخونید چون خیلی با آنالیز حقیقی فرق داره و قشنگتره. اول اینکه انتگرال گرفتن رو منحنیها، همانطور که ازش انتظار میره خطیه، روی منحنیها جمع پذیره. یعنی اگر دو تا منحنی را به هم پچسبونیم، به طوری که ته اولی روی سر دومی باشه، انتگرال جمع میشه. به سرعت منحنی بستگی نداره (یعنی اگر تابع منحنی را از بازه

$[a,b]$

به

$[c,d]$

با تغییر سرعت، منتقل کنیم تغییری در انتگرال ایجاد نمیشود) و مهمتر از همه تحت هموتوپی ناوردا است. یعنی اگر در دامنه تعریف تابع f، دو منحنی بسته (سر و ته یکی باشد) هموتوب باشند، انتگرال تغییری نمیکند.(لینک هموتوپی: Homotopy - Wikipedia, the free encyclopedia) درواقع استفاده از کوشی که kaleiodoscope به آن اشاره کرد، از همین به دست می آید. حال به چند نکته مهم اشاره میکنم:
نکته اول: برای نقطه

$a\in \mathbb{C}$

داریم:

$\int_{|w-a|=r}{(w-a)^ndw}=\begin{cases} 0 & \text{ if } n\not=-1 \\ 2\pi i & \text{ if } n= -1 \end{cases}$

(منظور از

$|w-a|=r$

دایره ای به مرکز a و شعاع r در جهت پادساعتگرد است.

نکته دوم : اگر

$\gamma$

یک منحنی بسته باشد و تابع تحلیلی (مشتقپذیر)

$f$

درون ناحیه ای که

$\gamma$

میسازد برای همه نقاط تعریف شده باشد، اولا

$\int_\gamma {f(w)dw}=0$

و ثانیا برای هر نقطه

$z$

تو این ناحیه و هر عدد صحیح

$k\geqslant 0$

داریم

$f^{(k)}(z)=\frac{k!}{2\pi i}\int_\gamma {\frac{f(w)dw}{(w-z)^{k+1}}}$

(منظور از

$f^{(k)}$

مشتق k ام f است). ببخشید. الان کار دارم. دو نکته بعدی را بعد میگم، بعد هم اون قانونا را اثبات میکنم.

seyed iman · 1390/10/8

پاسخ : تابع زتا (ریاضی ها ببیند)

اینا که سادس...اون یوتا ارو برا چی تعریف کردی؟و روابط رو از کجا آوردی؟

amir.ekhlasi · 1390/10/8

پاسخ : تابع زتا (ریاضی ها ببیند)

kaleiodoscope گفت

باشه. فقط یک نکته این که بعدا از باقیمانده (Residue) برای قطبها استفاده میکنم. حالا چون تو گفتی اینا را نمیگم...
تابع یوتا طبق رابطه 4 تعریف میشه. همگرا بودن اون انتگرال رو اون منحنی، به خاطر این است که درجه

$(-w)^{z}$

چند جمله ای است، ولی درجه

$e^w-1$

نمایی است. شاید این عکس بتونه بهتر اون منحنی گاما را توضیح بده. ولی جهت چرخشش برعکسه: http://s2.picofile.com/file/7228443331/Untitled2.png
نکته جالب اینجاست که برای اعداد صحیح

$k \geqslant 2$

، تابع

$(e^w-1)^{-1}(-w)^kw$

یک تابع تحلیلی در کل صفحه است و روی تمام نقاط تعریف میشه، پس

$I(k)=0$

. ولی خوب خیلی مهم نیست، چون بعدا با قطبهای تابع گاما ساده میشه...
برای رابطه پنجم چون برای هر n طبیعی،

$e^{-\pi i n}=e^{\pi i n}$

پس اگر طبق کوشی عمل کنیم و دو سر منحنی

$\gamma$

را به هم نزدیک کنیم و روی محور x ها بیاریم، انتگرالشون با هم ساده میشه. پس

$I(-n)=\int_\gamma{(e^w-1)^{-1}(-w)^{-n}\frac{dw}{w}}=(-1)^n\int_{|w|=\delta}{\frac{w}{e^w-1}\frac{dw}{w^{n+2}}}$

اما طبق رابطه سوم و نکته ای که تو پست قبل بهش اشاره کردم، سمت راست برابر است با

$2\pi i(-1)^n\frac{B_{n+1}}{(n+1)!}$

در مورد رابطه ششم، وقتی کوشی میزنیم و دو سر منحنی گاما را به محور x ها میل میدهیم، با توجه به اینکه تعریف کرده ایم که تابع arg از

$-\pi$

تا

$\pi$

متغیر است، خواهیم داشت

$I(z)=e^{\pi iz}\int_\delta^\infty{(e^t-1)^{-1}t^z\frac{dt}{t}} +\int_{|w|=\delta}{(e^w-1)^{-1}(-w)^z\frac{dw}{w}}-e^{-\pi iz}\int_\delta^\infty{(e^t-1)^{-1}t^z\frac{dt}{t}}$

وقتی

$\delta \to 0$

انتگرال وسطی به صفر میل میکند (واضحه؟). و از آنجا که سمت چپ ثابت است، خواهیم داشت:

$I(z)=(e^{\pi iz}-e^{-\pi iz})\int_0^\infty{\frac{t^{z-1}}{e^t-1}dt}=2i\sin (\pi z)\int_0^\infty{\frac{t^{z-1}}{e^t-1}dt}$

و این رابطه ششم را ثابت میکند. میریم سراغ تابع زتا. برای z هایی که

$Re(z)>1$

(قسمت حقیقی آنها از یک بزرگتر است) با تغییر متغیر

$t=ns$

داریم:

$\Gamma(z)=\int_0^\infty{t^{z-1}e^{-t}dt}=n^z\int_0^\infty{s^{z-1}e^{-ns}ds} \Rightarrow \frac{\Gamma(z)}{n^z}=\int_0^\infty{s^{z-1}e^{-ns}ds}$

پس طبق تعریف تابع زتا:

$\Gamma(z)\zeta(z)=\sum _{n=1}^\infty{\int_0^\infty{t^{z-1}e^{-nt}dt}}=\int_0^\infty{t^{z-1}(\sum_{n=1}^\infty{e^{-nt}})dt}=\int_0^\infty{t^{z-1}\frac{e^{-t}}{1-e^{-t}}dt}=\int_0^\infty{\frac{t^{z-1}}{e^t-1}dt}$

اما طبق رابطه ششم (تابع یوتا) داریم

$I(z)=2i\sin(\pi z)\Gamma(z)\zeta(z)$

پس طبق رابطه دوم تابع گاما داریم

$\zeta(z)=\frac{\Gamma(1-z)}{2\pi i}I(z)$

و این رابطه هفتم را ثابت میکنه. نکته قابل توجه اینجاست که با توجه به این رابطه، میتوان تابع زتا را برای کل اعداد مختلط بسط داد. چون فعلا این پست طولانی شد، بقیه را در پست بعد میگم.

seyed iman · 1390/10/8

پاسخ : تابع زتا (ریاضی ها ببیند)

آهان.
فقط یه چیزی از کجا فهمیدی باید تابعی مثل یوتا تعریف کنی؟

amir.ekhlasi · 1390/10/8

پاسخ : تابع زتا (ریاضی ها ببیند)

kaleiodoscope گفت

تابع یوتا تابع معروفیه (البته نه به حد توابع گاما، زتا،بتا و ...) چون خیلی جاها که میخواند به برنولی برسند، از این تابع میرسند. ادامه بحث را میدم:
اثبات رابطه یکی مونده به آخر از بقیه سخت تره. چون باید برای اون منحنی جدید تعریف کرد و بعد با انتگرال گرفتن از اون قضیه را ثابت کرد. من این رابطه را برای

$Re(z)<0$

ثابت میکنم. زیرا اگر این را ثابت کنم، طبق قضیه Uniqueness این قضیه برای تمامی مقادیر z درست است. مطابق شکل، منحنی

$\gamma_m$

را تعریف میکنیم. که در آن دایره کوچکی با شعاع

$\delta<\pi$

در جهت خلاف عقربه های ساعت میچرخد و دایره ای با شعاع کمی کمتر از

$(2m+1)\pi$

در جهت عقربه های ساعت میچرخد و دو پاره خط آنها را به هم وصل میکنند. (قسمت کمی از کمانهای دوایر حذف شده است که در حالت حدی، وقتی دو پاره خط را به هم نزدیک میکنیم، پدیدار میشوند.) (در شکل دوم به جای دایره، مربع کشیده شده که فرقی هم ندارد. ولی جهت چرخش دوباره برعکس است. )

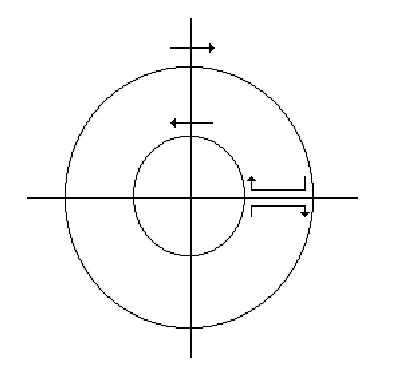
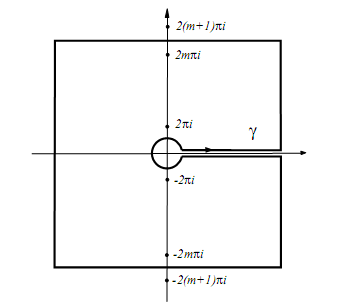
واضح است که برای عدد صحیح

$k\not=0$

،

$Res_{2\pi ik}((e^w-1)^{-1}\frac{(-w)^z}{w})=-(2\pi ik)^{z-1}$

. زیرا اگر تعریف کنیم

$f(w)=(e^w-1)^{-1}\frac{(-w)^z}{w}$

و

$g(w)=f(w)(w-2\pi ik)$

آنگاه

$g(2\pi ik)$

به

$-(2\pi ik)^{z-1}$

میل میکند. در اینصورت طبق قضیه باقیمانده (Residue theorem) داریم:

$-\frac{1}{2\pi i}\int_{\gamma_m}{(e^w-1)^{-1}(-w)^z\frac{dw}{w}}=\sum_{k=-1,1,...,-m,m,k\not=0}{Res_{2\pi i k}((e^w-1)^{-1}\frac{(-w)^z}{w})}=-\sum_{k=1}^m((2\pi ik)^{z-1}+(-2\pi ik)^{z-1})$

اما از آنجا که

$i^{z-1}+(-i)^{z-1}=\frac{1}{i}(e^{z\log i}-e^{z\log -i})=\frac{1}{i}(e^{\frac{\pi iz}{2}}-e^{-\frac{\pi iz}{2}})=2\sin(\frac{\pi z}{2})$

پس

$\frac{1}{2\pi i}\int_{\gamma_m}{(e^w-1)^{-1}(-w)^z\frac{dw}{w}}=2(2\pi)^{z-1}\sin(\frac{\pi z}{2})\sum_{k=1}^mk^{z-1}$

وقتی

$m \to \infty$

چون

$|\frac{(-w)^z}{w}|\leqslant |w|^{Re(z-1)}$

و فرض کردیم

$Re(z)<0$

، پس میتوان دید که انتگرال رو دایره بزرگتر به صفر میل میکند. پس اگر

$\gamma$

همان منحنیی باشد که قبلا فرض کرده بودیم، داریم

$\frac{1}{2\pi i}I(z)=\frac{1}{2\pi i}\int_\gamma{(e^w-1)^{-1}(-w)^z\frac{dw}{w}}=2(2\pi)^{z-1}\sin(\frac{\pi z}{2})\sum_{k=1}^\infty{k^{z-1}}= \\2(2\pi)^{z-1}\sin(\frac{\pi z}{2})\zeta(1-z )$

اما با استفاده از رابطه هفتم داریم

$\zeta(z)=2(2\pi)^{z-1}\sin(\frac{\pi z}{2})\Gamma(1-z)\zeta(1-z)$

رابطه آخر نیز به طور مستقیم از روابط پنجم و هفتم به دست میاید. حال بریم سراغ مسئله ای که در تاپیک مطرح شد. طبق دو رابطه آخر داریم:

$(-1)^{2n-1}\frac{B_{2n}}{2n}=\zeta(1-2n)=2(2\pi)^{-2n}(-1)^n\sin(\frac{\pi(1-2n)}{2})\Gamma(2n)\zeta(2n)=2(2\pi)^{-2n}(-1)^n(2n-1)!\zeta(2n)$

در نتیجه داریم

$\zeta(2n)=\frac{(2\pi)^{2n}(-1)^{n+1}B_{2n}}{2.(2n)!}$

seyed iman · 1390/10/10

پاسخ : تابع زتا (ریاضی ها ببیند)

دستت درد نکنه.واقعن مرسی که وقت گزاشتی اینو حل کردی.:77:
کامل مساله رو بستی!!من که دیگه روم نمیشه اون رابطه بازگشتی رو بزارم!!:182:
بجز آرفکن و بوآس از کجا باید آنالیز مختلط بخونیم؟فک نکنم تو فیزیک المپیاد بدرد بخوره ولی المپیاد کیلو چنده هر چیزی برای آدم جالبه ارزش یاد گرفتن داره!!
من فقط تا حالا تو فیزیک کوانتوم و برای انتگرال گرفتن های منفی بینهایت تا بی نهایت بدردم خورده و همچنین تو مکانیک آماری.خیلی کم.
ولی خییییییییییییییییییلی باحاله!!

amir.ekhlasi · 1390/10/10

پاسخ : تابع زتا (ریاضی ها ببیند)

من یه فایل pdf خیلی خوب دارم که واقعا قشنگ و ساده توضیح داده. این برای شروع خیلی خوبه: shabat-all .

seyed iman · 1390/10/12

پاسخ : تابع زتا (ریاضی ها ببیند)

دیگه چی؟
این خوب بود ولی زیاد نرفته بود سراغ کاربرد هاش .

seyed iman · 1391/2/26

پاسخ : تابع زتا (ریاضی ها ببیند)

واااااااااااااااااااااووووووو!!!!
بلخره شد!!روشم کامل کردم.بدون این جنگولک بازی ها(البته من عاششششششق این جنگولک بازی ها هستم) و فقط با تعاریف و بدون هیچ دانشی از انتگرال گیری مختلط اثباتش کردم!!خیلی خوشگل شد!!حالا اثباتشو میزارم.

تابع زتا (ریاضی ها ببیند)

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

New Member

New Member

New Member

Well-Known Member

New Member

Well-Known Member

New Member

New Member

Well-Known Member

New Member

Well-Known Member

New Member

Well-Known Member

New Member

Well-Known Member

Well-Known Member