تابع وجود ندارد!

Aref · 1392/10/12

ثابت کنید تابع پیوسته ی

$f : [0,1]\rightarrow \mathbb {R}^{\ge0}$

وجود ندارد که دارای سه خاصیت زیر باشد:

$\int_{0}^{1}f(x)\mathrm {d}x=1$

$\int_{0}^{1}xf(x)\mathrm {d}x=k$

$\int_{0}^{1}x^2f(x)\mathrm {d}x=k^2$

hkh74 · 1392/10/12

پاسخ : تابع وجود ندارد!

از یک طرف:

$\\1=\int_{0}^{1}f(x)\mathrm{d}x=\lim_{n\to\infty}\frac{1}{n}\sum_{i=0}^{n}f\left (\frac{i}{n} \right ) \\k=\int_{0}^{1}xf(x)\mathrm{d}x=\lim_{n\to\infty}\frac{1}{n^2}\sum_{i=0}^{n}if\left (\frac{i}{n} \right ) \\k^2=\int_{0}^{1}x^2f(x)\mathrm{d}x=\lim_{n\to\infty}\frac{1}{n^3}\sum_{i=0}^{n}i^2f\left (\frac{i}{n} \right )$

از طرف دیگه طبق نامساوی کوشی:

$\left (\frac{1}{n}\sum_{i=0}^{n}f\left (\frac{i}{n} \right ) \right )\left (\frac{1}{n^3}\sum_{i=0}^{n}i^2f\left (\frac{i}{n} \right ) \right )\geq \left (\frac{1}{n^2}\sum_{i=0}^{n}if\left (\frac{i}{n} \right ) \right )^2$

در دو طرف نامساوی n رو به بی‌نهایت میل می‌دیم و از سه‌تا رابطه‌ی اول استفاده می‌کنیم؛ به دست میاد در حالت حدی حالت تساوی کوشی اتفاق افتاده، همچنین ثابت می‌شه حالت تساوی کوشی در حالت حدی هم مثل حالت عادیه (همون اثباتی از کوشی که عبارت

$\left (\sum a_i^2 \right )\left (\sum b_i^2 \right )-\left (\sum a_ib_i \right )^2$

رو به صورت جمع تعدادی مربع کامل می‌نویسه برای این هم جواب می‌ده). حالت تساوی هم امکان نداره! تناقض!
ایشالا که جوب نداره!

Aref · 1392/10/12

پاسخ : تابع وجود ندارد!

ببین، ممکنه حالت تساوی در کوشی برقرار نباشه ولی حد که می گیریم، دو طرف به یک عدد میل کنند. اگر بخوایم از عبارت

$(\sum_{i=0}^{n}x_i^2).(\sum_{i=0}^{n}y_i^2)-(\sum_{i=0}^{n}x_iy_i)^2=\sum_{1\le i < j \le n} (x_iy_j-x_jy_i)^2$

باید ثابت کنیم که حد عبارت سمت راست صفر نیست. یعنی تا اینجا از نظر من مساله پیش نرفته.

hkh74 · 1392/10/12

پاسخ : تابع وجود ندارد!

وقتی حالت تساوی در بی‌نهایت اتفاق بیفته یعنی حد عبارت سمت راست صفر می‌شه... اگه موافقی که درسته، همین برای اثبات کافیه؛ یعنی تک‌تک جملاتش باید صفر باشن وگرنه چون یه جمله از یه جایی به بعد همیشه در اون عبارت ظاهر می‌شه (و اون عبارت بقیه‌ی جملاتش مثبتن) پس نمی‌تونه به صفر میل کنه.

Aref · 1392/10/12

پاسخ : تابع وجود ندارد!

آها یه کامنتی:
من الآن خودم غیر مستقیم ثابت کردم که اگر تابع کران پایین ناصفر داشته باشه مساله حله.

---- دو نوشته به هم متصل شده است ----

hkh74 گفت

نه موافق نیستم.

---- دو نوشته به هم متصل شده است ----

توی مخرج n به توان 8 داریم، که اصلا معلوم نیست اون حدی که می گی ناصفر باشه.

hkh74 · 1392/10/12

پاسخ : تابع وجود ندارد!

جوب داشت....!

خب یک راه دیگر: (اینو باید با دست باز تصحیح کنید!)

دو رابطه‌ی زیر از سه رابطه‌ی اصلی راحت به دست میان:

$\\=\lim_{n\to\infty}\left (\frac{1}{n^3}\sum_{i=0}^{n}i^2f\left (\frac{i}{n} \right ) \right )\lim_{n\to\infty}\left (\frac{1}{n}\sum_{i=0}^{n}f\left (\frac{i}{n} \right ) \right )-\lim_{n\to\infty}\left (\frac{1}{n^2}\sum_{i=0}^{n}if\left (\frac{i}{n} \right ) \right )^2 \\=\lim_{n\to\infty}\left (\left (\frac{1}{n^3}\sum_{i=0}^{n}i^2f\left (\frac{i}{n} \right ) \right )\left (\frac{1}{n}\sum_{i=0}^{n}f\left (\frac{i}{n} \right ) \right )-\left (\frac{1}{n^2}\sum_{i=0}^{n}if\left (\frac{i}{n} \right ) \right )^2 \right ) \\=\lim_{n\to\infty}\sum_{0\leq i\leq j\leq n}$

تعریف می‌کنیم:

$g(x)=(x-k)f(x)\mathrm{d}x,\; h(x)=\int_{0}^{x}g(t)\mathrm{d}t$

دو رابطه‌ی بالاتر تبدیل می‌شن به

$\\h(1)-h(0)=0\Rightarrow h(1)=h(0)=0 \\\int_{0}^{1}xh'(x)\mathrm{d}x=0\Rightarrow h(1)-\int_{0}^{1}h(x)\mathrm{d}x=0 \\\Rightarrow\int_{0}^{1}h(x)\mathrm{d}x=h(1)=h(0)=0$

طبق شهود هندسی‌ای که داریم (و اثبات‌پذیره) باید حداقل در دو نقطه (داخل بازه) مشتق h تغییر علامت بده (یا کلاً صفر باشه که امکان نداره) پس g در دو نقطه تغییر علامت می‌ده، پس f هم در یک نقطه تغییر علامت میده که تناقضه.

Aref · 1392/10/12

پاسخ : تابع وجود ندارد!

مرسی، درشته.

راه حل دیگر از نادر مستعان:

تابع f یک تابع توزیع احتمال است. طبق فرض،میانگین این توزیع برابر k است.
واریانس این تابع توزیع احتمال را محاسبه می کنیم:

$\int_{0}^{1}(x-k)^2f(x)\mathrm {d}x=\int_{0}^{1}x^2f(x)\mathrm {d}x-2k\int_{0}^{1}xf(x)\mathrm {d}x+k^2\int_{0}^{1}f(x)\mathrm {d}x=0$

اما این تناقضی است بس آشکار، چرا که واریانس همواره ناصفر است.

hkh74 · 1392/10/12

پاسخ : تابع وجود ندارد!

جوب اولی احتمالاً این‌جوری برطرف می‌شه: (می‌تونید فرض کنید این راه خیلی بهتر (و البته کوتاه‌تر!) از راه آقای مستعانه!)

$0=k^2\times1-k\times k \\=\lim_{n\to\infty}\left (\frac{1}{n^3}\sum_{i=0}^{n}i^2f\left (\frac{i}{n} \right ) \right )\lim_{n\to\infty}\left (\frac{1}{n}\sum_{i=0}^{n}f\left (\frac{i}{n} \right ) \right )-\lim_{n\to\infty}\left (\frac{1}{n^2}\sum_{i=0}^{n}if\left (\frac{i}{n} \right ) \right )^2 \\=\lim_{n\to\infty}\left (\left (\frac{1}{n^3}\sum_{i=0}^{n}i^2f\left (\frac{i}{n} \right ) \right )\left (\frac{1}{n}\sum_{i=0}^{n}f\left (\frac{i}{n} \right ) \right )-\left (\frac{1}{n^2}\sum_{i=0}^{n}if\left (\frac{i}{n} \right ) \right )^2 \right ) \\=\frac{1}{2}\lim_{n\to\infty}\sum_{i=0}^{n}\sum_{j=0}^{n}\frac{1}{n^2}f\left (\frac{i}{n} \right )f\left (\frac{j}{n} \right )\left ( \frac{i}{n}-\frac{j}{n} \right )^2$

تعریف کنید

$g(x,y)=f(x)f(y)(x-y)^2$

پس:

$\frac{1}{2}\lim_{n\to\infty}\sum_{i=0}^{n}\sum_{j=0}^{n}\frac{1}{n^2}g\left (\frac{i}{n},\frac{j}{n} \right )=0$

ولی طرف چپ داره به حجم زیر نمودار g در فضای سه بعدی میل می‌کنه که ناصفره. تناقض!

Aref · 1392/10/12

پاسخ : تابع وجود ندارد!

احسنت.

برای حالتی که

$\forall x :f(x)>0$

من یه ایده ی دیگه دارم که اون هم درخور توجه می باشد:

تابع

$f$

روی بازه ی بسته ی

$[0,1]$

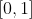یک کران پایین مثبت دارد. این کران پایین را

$k$

بگیرید.

طبق فرض مساله همون طور که گفته شد داریم:

$\int_{0}^{1}x^2f(x)\mathrm{d}x.\int_{0}^{1}f(x)\mathrm{d}x-(\int_{0}^{1}xf(x)\mathrm{d}x)^2=\lim_{n\to\infty}\sum_{1\le i < j \le n}\frac{f(\frac{i}{n})f(\frac{j}{n})}{n^4}(i-j)^2$

اگر به جای تابع

$f$

تابع

$\forall x \in [0,1]:g(x)=1$

رو در عبارت بالا قرار دهیم، به دست می آید:

$\lim_{n\to\infty}\sum_{1\le i < j \le n}\frac{(i-j)^2}{n^4}=\frac {1}{12}$

بنابراین چون حد گرفتن خاصیت حفظ نابرابری رو داره، پس

$\int_{0}^{1}x^2f(x)\mathrm{d}x.\int_{0}^{1}f(x)\mathrm{d}x-(\int_{0}^{1}xf(x)\mathrm{d}x)^2\ge \frac {k^2}{12}$

ولی طرف سمت چپ صفر بود. که این هم تناقض است.

---- دو نوشته به هم متصل شده است ----

اگر فرض کنیم تابع

$f$

روی بازه ی

$[a,b]$

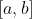مقدارش مثبت است؛ تعریف می کنیم:

$h:[0,1]\rightarrow R$

$h(x)=\left\{\begin{matrix} \frac {1}{b-a} & \mathrm{if}\; x\in [a,b]\\ 0 & \mathrm {Otherwise} \end{matrix}\right.$

به وضوح تابع

$h$

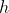انتگرال پذیر است و داریم:

$\int_{0}^{1}h(x)\mathrm{d}x=1$

$\int_{0}^{1}xh(x)\mathrm{d}x=\frac{a+b}{2}$

$\int_{0}^{1}x^2h(x)\mathrm{d}x=\frac{a^2+ab+b^2}{3}$

از طرفی داریم:

$\int_{0}^{1}x^2h(x)\mathrm{d}x.\int_{0}^{1}h(x)\mathrm{d}x-(\int_{0}^{1}xh(x)\mathrm{d}x)^2=\sum_{1\le i < j \le n}\frac {h(\frac{i}{n})h(\frac{j}{n})}{n^4}(j - i)^2$

اما عبارت سمت چپ را قبلا محاسبه کرده ایم:

$\int_{0}^{1}x^2h(x)\mathrm{d}x.\int_{0}^{1}h(x)\mathrm{d}x-(\int_{0}^{1}xh(x)\mathrm{d}x)^2=\frac{(a-b)^2}{12}$

حال می دانیم که تابع

$f$

روی بازه ی

$[a,b]$

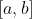کران پایین مثبتی مانند

$k$

دارد.

بنابراین:

$\forall x \in [0,1]:f(x)\ge k(b-a)h(x)$

پس:

$\int_{0}^{1}x^2f(x)\mathrm {d}x.\int_{0}^{1}f(x)\mathrm {d}x-(\int_{0}^{1}xf(x)\mathrm {d}x)^2\ge \frac {k^2(b-a)^4}{12}$

که تناقض است. پس حکم در حالت کلی ثابت شد و چنین تابعی وجود ندارد.

تابع وجود ندارد!

Aref

New Member

hkh74

New Member

Aref

New Member

hkh74

New Member

Aref

New Member

hkh74

New Member

Aref

New Member

hkh74

New Member

Aref

New Member