تجزیه یک چندجمله ای
- شروع کننده موضوع mahdigh2
- تاریخ شروع
- برچسپ ها المپیاد المپیاد ریاضی تحویل ناپذیر تشریحی دبیرستان راهنمایی ریاضی ریشه ریشه صحیح سوال عدد اول مجموعه پاسخ تشریحی چند جمله ای چندجمله ای کتاب
پاسخ : تجزیه یک چندجمله ای
150 مساله پیشنهادی برای المپیادهای جهانی ریاضی به همراه راهنمایی و حل تشریحی
پدیدآورنده : فرشید الموتی
ناشر : موسسه فرهنگی انتشاراتی پیش دانشگاهیان
تعداد صفحات : 162
تاریخ نشر : 1377/2/8
"در این مجموعه تلاش شده، ذیل سه بخش مهم‌ترین مباحثی كه در المپیادهای ریاضی مطرح میشود فراهم آید .در بخش اول 150مسئله متنوع برای المپیادهای مختلف جهانی پیشنهاد شده است .بخش دوم، متضمن راهنمایی‌هایی برای حل مسائل است .در بخش پایانی پاسخ تشریحی مسائل مطرح شده در بخش اول آمده است .دبیران ریاضی، دانش‌آموزان مقطع دبیرستان و دانشجویان علاقه مند به مفاهیم ریاضی از مخاطبان این مجموعه به شمار می‌آیند."
150 مساله پیشنهادی برای المپیادهای جهانی ریاضی به همراه راهنمایی و حل تشریحی
پدیدآورنده : فرشید الموتی
ناشر : موسسه فرهنگی انتشاراتی پیش دانشگاهیان
تعداد صفحات : 162
تاریخ نشر : 1377/2/8
"در این مجموعه تلاش شده، ذیل سه بخش مهم‌ترین مباحثی كه در المپیادهای ریاضی مطرح میشود فراهم آید .در بخش اول 150مسئله متنوع برای المپیادهای مختلف جهانی پیشنهاد شده است .بخش دوم، متضمن راهنمایی‌هایی برای حل مسائل است .در بخش پایانی پاسخ تشریحی مسائل مطرح شده در بخش اول آمده است .دبیران ریاضی، دانش‌آموزان مقطع دبیرستان و دانشجویان علاقه مند به مفاهیم ریاضی از مخاطبان این مجموعه به شمار می‌آیند."
آخرین ویرایش توسط مدیر
- ارسال ها
- 159
- لایک ها
- 282
- امتیاز
- 0
پاسخ : تجزیه یک چندجمله ای
لم: تعمیم محک آیزنشتاین: فرض کنید
اگر عدد اول
موجود باشد بطوری که
و
وجود داشته باشد که
و
آنگاه چندجمله ای
عاملی دارد که تحویل ناپذیر است و درجه اش حداقل
است.
اثبات لم فوق به مانند اثبات خود محک آیزنشتاین است.
حال دقت کنید که برای
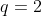و
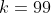چند جمله ای فوق در شرایط لم صدق میکند پس عاملی دارد که تحویل ناپذیر است و درجه اش حداقل 99 است.
بنابرین یا چند جمله ای خود تحویل ناپذیر است یا یک عامل تحویل ناپذیر از درجه 99 دارد. اما اگر چنین باشد پس یک ریشه صحیح هم دارد زیرا در تجزیه آن یک چند جمله ای درجه 99 ظاهر میشود پس درجه خارج قسمت دقیقاً 1 است. بنابرین توسط چند جمله ای صحیح الضرایبی با درجه یک عاد میشود پس ریشه صحیح دارد.
حال میخواهیم ثابت کنیم که چند جمله ای تجزیه ناپذیر است . فرض خلف کنید که این طور نباشد پس ریشه ای صحیح دارد.
همچنین دقت کنید که چون ضریب جمله ثابت چند جمله ای 2 است پس اگر این چند جمله ای ریشه ای صحیح ناصفر داشته باشد مانند
آنگاه
زیرا اگر
آنگاه دو طرف بر
بخش پذیر است که با حذف جملات شامل
آنگاه تنها ضریب جمله ثابت میماند.
پس
یکی از 0و1و-1و2و-2 است. که با جایگذاری در چندجمله ای به دست می آوریم که هیچ کدام صدق نمیکنند. پس به تناقض رسیدیم، یعنی چندجمله ای تجزیه ناپذیر است.
لم: تعمیم محک آیزنشتاین: فرض کنید
اثبات لم فوق به مانند اثبات خود محک آیزنشتاین است.
حال دقت کنید که برای
بنابرین یا چند جمله ای خود تحویل ناپذیر است یا یک عامل تحویل ناپذیر از درجه 99 دارد. اما اگر چنین باشد پس یک ریشه صحیح هم دارد زیرا در تجزیه آن یک چند جمله ای درجه 99 ظاهر میشود پس درجه خارج قسمت دقیقاً 1 است. بنابرین توسط چند جمله ای صحیح الضرایبی با درجه یک عاد میشود پس ریشه صحیح دارد.
حال میخواهیم ثابت کنیم که چند جمله ای تجزیه ناپذیر است . فرض خلف کنید که این طور نباشد پس ریشه ای صحیح دارد.
همچنین دقت کنید که چون ضریب جمله ثابت چند جمله ای 2 است پس اگر این چند جمله ای ریشه ای صحیح ناصفر داشته باشد مانند
پس
آخرین ویرایش توسط مدیر