ثابت کنید
- شروع کننده موضوع Antimony
- تاریخ شروع
- برچسپ ها اثبات استفاده اعداد بخش پذيري سوال فرمول نویسی نظریه اعداد
پاسخ : ثابت کنید
سوال اولتون كه منظورتونو از ساده كردن نفهميدم.
ببينيد سيگما فقط يه تعريفه براي ساده تر نوشتن و كار خاصي انجام نميده. همون عبارتو ميشه اينجوري هم نوشت:


آیا با ساده کردن
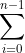 از طرفین، میشه نتیجه گرفت:
از طرفین، میشه نتیجه گرفت:
 ؟؟؟؟؟؟؟
؟؟؟؟؟؟؟
و اگر بله، چرا
 ؟؟؟؟؟؟؟؟؟؟؟؟؟
؟؟؟؟؟؟؟؟؟؟؟؟؟
+ راه حل دیگه ای هم بجز
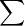 داره؟
داره؟
و اگر بله، چرا
+ راه حل دیگه ای هم بجز
ببينيد سيگما فقط يه تعريفه براي ساده تر نوشتن و كار خاصي انجام نميده. همون عبارتو ميشه اينجوري هم نوشت:
براي سوال دومتون هم ميشه اينجوري گفت:


- ارسال ها
- 288
- لایک ها
- 154
- امتیاز
- 43
پاسخ : ثابت کنید
اون قسمتاي اخر راهتونو چكار كرديد؟ ما تو بخش پذيري اين قوانيني را كه شما استفاده كرديد نداريم براي اثبات حكم ميتونيم به صورت زير عمل كنيم
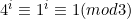

اگه منظورتون
 هست ، بر 3 بخش پذیر نیست. با مثال نقض میتونید اثبات کنید (
هست ، بر 3 بخش پذیر نیست. با مثال نقض میتونید اثبات کنید (
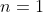 )
)
...
ولی اگه منظورتون
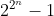 :
:
فرض کنیم
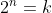
در نتیجه میشه
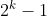
ما میدونیم k عددی زوجه چون
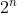 زوجه
زوجه
2 به توان یه عدد زوج، بصورت
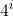 نوشته میشه
نوشته میشه
پس حکم جدید میشه:
ثابت کنید
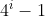 بر 3 بخش پذیر است
بر 3 بخش پذیر است
یعنی
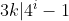

چون

پس حکم به ازای هر
 برقراره
برقراره
(((اگه درست گفته باشم!)))
...
بهتر بود با فرمول نویسی صورت سوال رو مینوشتید
...
ولی اگه منظورتون
فرض کنیم
در نتیجه میشه
ما میدونیم k عددی زوجه چون
2 به توان یه عدد زوج، بصورت
پس حکم جدید میشه:
ثابت کنید
یعنی
چون
پس حکم به ازای هر
(((اگه درست گفته باشم!)))
...
بهتر بود با فرمول نویسی صورت سوال رو مینوشتید
آخرین ویرایش توسط مدیر
پاسخ : ثابت کنید
اثباتتون درست نیست. دو رابطه ی
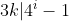 و
و
 هم ارز نیستند در ضمن لزوما
هم ارز نیستند در ضمن لزوما
 بر 4 بخشپذیر نیست و حتی اگه بخشپذیر باشه هم نمی تونید نتیجه بگیرید که
بر 4 بخشپذیر نیست و حتی اگه بخشپذیر باشه هم نمی تونید نتیجه بگیرید که
 . همونجایی که گفتید باید ثابت کنیم
. همونجایی که گفتید باید ثابت کنیم
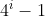 بر سه بخشپذیره یه چاق و لاغر بزنید سوال حل میشه.
بر سه بخشپذیره یه چاق و لاغر بزنید سوال حل میشه.
اگه منظورتون
 هست ، بر 3 بخش پذیر نیست. با مثال نقض میتونید اثبات کنید (
هست ، بر 3 بخش پذیر نیست. با مثال نقض میتونید اثبات کنید (
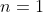 )
)
...
ولی اگه منظورتون
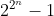 :
:
فرض کنیم
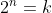
در نتیجه میشه
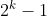
ما میدونیم k عددی زوجه چون
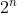 زوجه
زوجه
2 به توان یه عدد زوج، بصورت
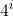 نوشته میشه
نوشته میشه
پس حکم جدید میشه:
ثابت کنید
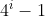 بر 3 بخش پذیر است
بر 3 بخش پذیر است
یعنی
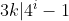

چون

پس حکم به ازای هر
 برقراره
برقراره
(((اگه درست گفته باشم!)))
...
بهتر بود با فرمول نویسی صورت سوال رو مینوشتید
...
ولی اگه منظورتون
فرض کنیم
در نتیجه میشه
ما میدونیم k عددی زوجه چون
2 به توان یه عدد زوج، بصورت
پس حکم جدید میشه:
ثابت کنید
یعنی
چون
پس حکم به ازای هر
(((اگه درست گفته باشم!)))
...
بهتر بود با فرمول نویسی صورت سوال رو مینوشتید
