حد
پاسخ : حد
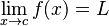
در کل مفهوم حد:که اگر x به‌اندازهٔ کافی به c نزدیک شد مقدار f(x) به‌اندازهٔ دلخواه به L نزدیک بشه.
حالا حد (تابع) که به سمت بی نهایت میل کنه
مثلا
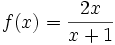
میایم متغیر x رو بی نهایت در نظر میگیریم به زبون ساده تر. حالا در مخرج داریم بی نهایت به علاوه 1 . تاثیری داره؟!نداره که! در صورت هم 2 در بی نهایت ضربمیشه.
حالا کل کسر داره به عدد 2 نزدیک میشه!یعنی :
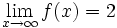
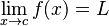
در کل مفهوم حد:که اگر x به‌اندازهٔ کافی به c نزدیک شد مقدار f(x) به‌اندازهٔ دلخواه به L نزدیک بشه.
حالا حد (تابع) که به سمت بی نهایت میل کنه
مثلا
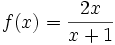
میایم متغیر x رو بی نهایت در نظر میگیریم به زبون ساده تر. حالا در مخرج داریم بی نهایت به علاوه 1 . تاثیری داره؟!نداره که! در صورت هم 2 در بی نهایت ضربمیشه.
حالا کل کسر داره به عدد 2 نزدیک میشه!یعنی :
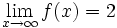
پاسخ : حد
حد تابع زمانی که متغیر به سمت بی نهایت میل میکنه.
ببینید اولا" باید بدونیم بی نهایت عدد نیست.یک مفهوم حدی است به معنای هر چه بزرگتر.به عبارت دقیق تر گوییم عدد x به سمت بی نهایت میل میکند اگر و تنها اگر به ازای هر عدد مثبتی مانند N داشته باشیم
.
حالا تابع زیر رو در نظر بگیرید.در این تابع میتونیم مقادیر تابع رو به اندازه ی دلخواه به صفر نزدیک کنیم به شرط آن که x به اندازه ی کافی بزرگ شده باشد.در واقع تنها فرق حد تابع زمانی که متغیر به بی نهایت میل میکنه با حد تابع زمانی که متغیر به عدد خاصی میل میکنه این هست که در زمان اول اگر متغیر رو به اندازه ی کافی به اون عدد نزدیک میکنیم تامقدار تابع به عدد حد نزدیک بشه اما در مورد دوم اگر متغیر رو به اندازه ی کافی بزرگ کنیم مقدار تابع به حاصل حد تابع نزدیک میشه.
به طور وارون بررسی میکنیم .در مورد اول برای اینکه مقدار تابع به خد تابع نزدیک بشه باید متغیر رو به عدد خاصی نزدیک کنیم اما در مورد بعد اگر بخواهیم مقدار تابع رو به حد تابع نزدیک کنیم باید متغیر رو هر چه بیشتر بزرگ کنیم .
=\frac{1}{x})
اکنون موارد بالا رو در مورد این تابع بررسی میکنیم.من به متغیر x از مقادیر بزرگ تر از 2 و مقادیر کوچک تر از 2 اعدادی نسبت میدهم (در ماشین حساب انجام بده)مشاهده میکنم که هر قدر جلو تر میرویم چه مقادیر بزرگ تر چه مقادیر کوچک تر مقدار تابع به یک دوم نزدیک میشه و بالعکس برای اینکه مقدار تابع به اندازه ی دلخواه به یک دوم نزدیک بشه باید اعدادم به اندازه ی کافی به 2 نزدیک شده باشه .مثلا" برای اینکه 1/. از یک دوم فاصله داشته باشم باید فاصله ی اعداد از 2 کمتر از 5/. باشد.پس طبق تعریف دوستمون میتونم بنویسم :
اما مشاهده میکنم اگر مقادیر x رو هرچه بیشتر بزرگ تر کنم مقدار تابع بیشتر به صفر نزدیک میشود و بالعکس(مطابق بالا استدلال کن)پس این دفعه مینویسم:
در مورد حد وقتی که تابع به بی نهایت میل میکنه هم اگر اشکال داشتی بپرس.
حد تابع زمانی که متغیر به سمت بی نهایت میل میکنه.
ببینید اولا" باید بدونیم بی نهایت عدد نیست.یک مفهوم حدی است به معنای هر چه بزرگتر.به عبارت دقیق تر گوییم عدد x به سمت بی نهایت میل میکند اگر و تنها اگر به ازای هر عدد مثبتی مانند N داشته باشیم
حالا تابع زیر رو در نظر بگیرید.در این تابع میتونیم مقادیر تابع رو به اندازه ی دلخواه به صفر نزدیک کنیم به شرط آن که x به اندازه ی کافی بزرگ شده باشد.در واقع تنها فرق حد تابع زمانی که متغیر به بی نهایت میل میکنه با حد تابع زمانی که متغیر به عدد خاصی میل میکنه این هست که در زمان اول اگر متغیر رو به اندازه ی کافی به اون عدد نزدیک میکنیم تامقدار تابع به عدد حد نزدیک بشه اما در مورد دوم اگر متغیر رو به اندازه ی کافی بزرگ کنیم مقدار تابع به حاصل حد تابع نزدیک میشه.
به طور وارون بررسی میکنیم .در مورد اول برای اینکه مقدار تابع به خد تابع نزدیک بشه باید متغیر رو به عدد خاصی نزدیک کنیم اما در مورد بعد اگر بخواهیم مقدار تابع رو به حد تابع نزدیک کنیم باید متغیر رو هر چه بیشتر بزرگ کنیم .
اکنون موارد بالا رو در مورد این تابع بررسی میکنیم.من به متغیر x از مقادیر بزرگ تر از 2 و مقادیر کوچک تر از 2 اعدادی نسبت میدهم (در ماشین حساب انجام بده)مشاهده میکنم که هر قدر جلو تر میرویم چه مقادیر بزرگ تر چه مقادیر کوچک تر مقدار تابع به یک دوم نزدیک میشه و بالعکس برای اینکه مقدار تابع به اندازه ی دلخواه به یک دوم نزدیک بشه باید اعدادم به اندازه ی کافی به 2 نزدیک شده باشه .مثلا" برای اینکه 1/. از یک دوم فاصله داشته باشم باید فاصله ی اعداد از 2 کمتر از 5/. باشد.پس طبق تعریف دوستمون میتونم بنویسم :
اما مشاهده میکنم اگر مقادیر x رو هرچه بیشتر بزرگ تر کنم مقدار تابع بیشتر به صفر نزدیک میشود و بالعکس(مطابق بالا استدلال کن)پس این دفعه مینویسم:
در مورد حد وقتی که تابع به بی نهایت میل میکنه هم اگر اشکال داشتی بپرس.
پاسخ : حد
ببینید...
توماس خیلی طولانیه....
اینجا نمیشه اصلا گذاشتش
اینو میگم. اگر خیلی خوب جا نیفتاد پیام خصوصی بدین، توماس رو بفرستمش.
از اپسیلون، ε، برای نشان دادن یک مقدار مثبت بسیار کوچک باستفاده میشده. هنگامی که «f(x) به‌اندازهٔ دلخواه به L نزدیک میشود» به این معنی است که مقدار f(x) کم کم در بازهٔ (L - ε, L + ε) جای می‌گیرد. با کمک قدر مطلق چنین می‌نویسیم: |f(x) - L| < ε.
عبارت «هنگامی که x به‌اندازهٔ کافی به c نزدیک میشود» به این معنی است که مقدارهای حقیقی از x را در نظر داریم که فاصلهٔ آن‌ها از c کمتر از عدد مثبت دلتا، δ باشد. یعنی x عضو یکی از دو بازهٔ (c - δ, c) یا (c, c + δ) است، نوشتار ریاضی این عبارت چنین است: ۰ < |x - c| < δ. نامساوی نخست یعنی فاصلهٔ میان c و x بیشتر از صفر است و x ≠ c است در حالی که نامساوی دوم می‌گوید فاصلهٔ x از c کمتر از δ است
توجه داشته باشید که تعریف بالا برای حد می‌تواند درست باشد حتی اگر
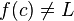باشد. در حقیقت حتی نیازی نیست که f(x) در c تعریف شده باشد.
برای نمونه اگر داشته باشیم:
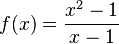
:f(1) تعریف نشده‌است (بخش بر صفر) حال هر چه x به ۱ نزدیک میشود، f(x)
[TABLE="class: wikitable"]
[TR]
[TD]f(۰٫۹)[/TD]
[TD]f(۰٫۹۹)[/TD]
[TD]f(۰٫۹۹۹)[/TD]
[TD]f(۱٫۰)[/TD]
[TD]f(۱٫۰۰۱)[/TD]
[TD]f(۱٫۰۱)[/TD]
[TD]f(۱.۱)[/TD]
[/TR]
[TR]
[TD]۱٫۹۰۰[/TD]
[TD]۱٫۹۹۰[/TD]
[TD]۱٫۹۹۹[/TD]
[TD]⇒ تعریف نشده ⇐[/TD]
[TD]۲٫۰۰۱[/TD]
[TD]۲٫۰۱۰[/TD]
[TD]۲٫۱۰۰[/TD]
[/TR]
[/TABLE]
بنابراین، مقدار f(x) به ۲ نزدیک میشود هرگاه بتوانیم x را به‌اندازهٔ کافی به ۱ نزدیک کنیم.
به عبارت دیگر
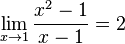
یک تابع علاوه بر داشتن حد در مقدارهای معین، می‌تواند در بی نهایت هم دارای حد باشد. برای نمونه:
هرگاه x مقدارهای بی نهایت بزرگ به خود گیرد، مقدار f(x) به سوی ۲ کشیده میشود. در این حالت می‌گوییم حد f(x) به ازای xهای رو به بی نهایت، برابر ۲ است. بیان ریاضی این گفته چنین است
اثبات:
گوییم
در نقطه‌ای مانند
دارای حد
است اگر به ازای هر عدد مثبت
عدد مثبتی مثل
موجود باشد به طوری که اگر
، آنگاه
.
به عبارت دیگر برای هر
یک
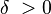وجود داشته باشد، که برای هر
با خاصیت
، داشته باشیم
.
برای تعریف غیرصوری باید گفت حد تابع
،
است اگر وقتی
،
به حد
نزدیک بشود، یا
در
دارای حد
است، اگر هنگامی که
به
میل میکند،
به
نزدیک شود.
اگر مفاهیم اولیه تابع رو احاطه کامل داشته باشید حله...
چیز خاصی نداره...
درواقع بیان ساده:اینه که میخواد به یه چیز برسه اما نمیرسه و نزدیک اون میشه.
که میگن به سمت اون میل میکنه...
ببینید...
توماس خیلی طولانیه....
اینجا نمیشه اصلا گذاشتش
اینو میگم. اگر خیلی خوب جا نیفتاد پیام خصوصی بدین، توماس رو بفرستمش.
از اپسیلون، ε، برای نشان دادن یک مقدار مثبت بسیار کوچک باستفاده میشده. هنگامی که «f(x) به‌اندازهٔ دلخواه به L نزدیک میشود» به این معنی است که مقدار f(x) کم کم در بازهٔ (L - ε, L + ε) جای می‌گیرد. با کمک قدر مطلق چنین می‌نویسیم: |f(x) - L| < ε.
عبارت «هنگامی که x به‌اندازهٔ کافی به c نزدیک میشود» به این معنی است که مقدارهای حقیقی از x را در نظر داریم که فاصلهٔ آن‌ها از c کمتر از عدد مثبت دلتا، δ باشد. یعنی x عضو یکی از دو بازهٔ (c - δ, c) یا (c, c + δ) است، نوشتار ریاضی این عبارت چنین است: ۰ < |x - c| < δ. نامساوی نخست یعنی فاصلهٔ میان c و x بیشتر از صفر است و x ≠ c است در حالی که نامساوی دوم می‌گوید فاصلهٔ x از c کمتر از δ است
توجه داشته باشید که تعریف بالا برای حد می‌تواند درست باشد حتی اگر
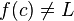
برای نمونه اگر داشته باشیم:
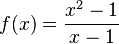
:f(1) تعریف نشده‌است (بخش بر صفر) حال هر چه x به ۱ نزدیک میشود، f(x)
[TABLE="class: wikitable"]
[TR]
[TD]f(۰٫۹)[/TD]
[TD]f(۰٫۹۹)[/TD]
[TD]f(۰٫۹۹۹)[/TD]
[TD]f(۱٫۰)[/TD]
[TD]f(۱٫۰۰۱)[/TD]
[TD]f(۱٫۰۱)[/TD]
[TD]f(۱.۱)[/TD]
[/TR]
[TR]
[TD]۱٫۹۰۰[/TD]
[TD]۱٫۹۹۰[/TD]
[TD]۱٫۹۹۹[/TD]
[TD]⇒ تعریف نشده ⇐[/TD]
[TD]۲٫۰۰۱[/TD]
[TD]۲٫۰۱۰[/TD]
[TD]۲٫۱۰۰[/TD]
[/TR]
[/TABLE]
بنابراین، مقدار f(x) به ۲ نزدیک میشود هرگاه بتوانیم x را به‌اندازهٔ کافی به ۱ نزدیک کنیم.
به عبارت دیگر
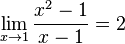
یک تابع علاوه بر داشتن حد در مقدارهای معین، می‌تواند در بی نهایت هم دارای حد باشد. برای نمونه:
- f(۱۰۰) = ۱٫۹۹۰۰
- f(۱۰۰۰) = ۱٫۹۹۹۰
- f(۱۰۰۰۰) = ۱٫۹۹۹۹۰
هرگاه x مقدارهای بی نهایت بزرگ به خود گیرد، مقدار f(x) به سوی ۲ کشیده میشود. در این حالت می‌گوییم حد f(x) به ازای xهای رو به بی نهایت، برابر ۲ است. بیان ریاضی این گفته چنین است
اثبات:
گوییم
به عبارت دیگر برای هر
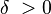
برای تعریف غیرصوری باید گفت حد تابع
اگر مفاهیم اولیه تابع رو احاطه کامل داشته باشید حله...
چیز خاصی نداره...
درواقع بیان ساده:اینه که میخواد به یه چیز برسه اما نمیرسه و نزدیک اون میشه.
که میگن به سمت اون میل میکنه...