سوالي از نامساوي

Olympiad · 1389/1/16

اگر

$x,y,z$

اعدادي حقيقي و مثبت باشند كه

$x+y+z=xyz$

. ثابت كنيد :

$\frac{1}{\sqrt{1+x^2}}+\frac{1}{\sqrt{1+y^2}}+\frac{1}{\sqrt{1+z^2}}\leq \frac{3}{2}$

abdi · 1389/1/16

از تغيير متغير

$x=tan(a) , y=tan(b) , z=tan(c)$

استفاده كنيد.

Aref · 1389/3/17

راه حل دوم:
تابع

$f:\mathbb{R^+}\rightarrow \mathbb{R^+}$

را با ضابطه ی

$f(x)=\frac{1}{\sqrt{1+x^2}}$

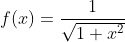تعریف کنید. این تابع محدب است.(اگه خواستی اثباتشو واست می نویسم)طبق نابرابری ینسن:

$\frac{1}{\sqrt{1+x^2}}+\frac{1}{\sqrt{1+y^2}}+\frac{1}{\sqrt{1+z^2}}=f(x)+f(y)+f(z)\leq 3f(\frac{x+y+z}{3})$

پس باید ثابت کنیم:

$\frac{1}{\sqrt{1+(\frac{x+y+z}{3})^2}}\leq \frac{1}{2}$

که معادل است با:

$(x+y+z)^2\geq 27$

که از نابرابری

$(x+y+z)^3\geq (3(xyz)^\frac{1}{3})^3=27(x+y+z)$

به دست می آید.

M_Sharifi · 1389/3/17

Aref گفت

اولا که تابع

$f(x)=\frac{1}{\sqrt{1+x^2}}$

تا یه جایی مقعره، بعدش محدب میشه.
ثانیا اگه محدب هم باشه، جهت نابرابری که شما به کار بردید باید برعکس بشه.

Aref · 1389/3/17

محدبی که من میگم با محدب توی صفا یکی نیست دقیقا برعکسشه

M_Sharifi · 1389/3/17

Aref گفت

با اون تعریف هم فقط برای

$0<x\leq\sqrt2$

میشه ینسن رو به کار برد. چون بعدش تقعر تابع تغییر میکنه.

Aref · 1389/3/19

$a=\frac{1}{x},b=\frac{1}{y},c=\frac{1}{z}\Rightarrow ab+bc+ca=1$

نابرابری به صورت

$\frac{a}{\sqrt{1+a^2}}+\frac{b}{\sqrt{1+b^2}}+\frac{c}{\sqrt{1+c^2}}\leq \frac{3}{2}$

در می آید.
حالا داریم:

$1+a^2=ab+bc+ca+a^2=(a+b)(a+c)$

(و به طور مشابه برای b,c) پس باید ثابت کنیم:

$\sum \frac{a}{\sqrt{(a+b)(a+c)}}\leq \frac{3}{2}$

با استفاده از نابرابری واسطه ی حسابی هندسی داریم:

$\sum \frac{a}{\sqrt{(a+b)(a+c)}}\leq \frac{1}{2}\sum \frac{a}{a+b}+\frac{1}{2}\sum \frac{a}{a+c}=\frac{3}{2}$

و حکم خواسته شده نتیجه می شود.

سوالي از نامساوي

Olympiad

New Member

abdi

New Member

Aref

New Member

M_Sharifi

راهبر ریاضی

Aref

New Member

M_Sharifi

راهبر ریاضی

Aref

New Member