پاسخ : لیگ جبر - هفته صفر الف (آزمایشی)
دیشب می خواستم دیگه برم بخوابم به خاطر همین خلاصه نوشتم ولی از این به بعد سعی می کنم کامل بنویسم.
3- سوال خیلی قشنگی بود.
رابطه ی
 را
را
 می نامیم. ابتدا واضح است که
می نامیم. ابتدا واضح است که
 نمی تواند متحد با صفر باشد. پس حداقل یک
نمی تواند متحد با صفر باشد. پس حداقل یک
 حقیقی وجود دارد که
حقیقی وجود دارد که
 باشد.
باشد.
 نتیجه می دهد:
نتیجه می دهد:
 پس
پس
 پوشاست. حال داریم:
پوشاست. حال داریم:
 با جایگذاری این رابطه در صورت سوال و
با جایگذاری این رابطه در صورت سوال و
 داریم:
داریم:


با استفاده از اینکه
 پوشاست داریم
پوشاست داریم
 و با جایگذاری این رابطه در صورت سوال بدست می آید
و با جایگذاری این رابطه در صورت سوال بدست می آید
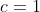 پس
پس
 می باشد.
می باشد.
---- دو نوشته به هم متصل شده است ----
٥- قرار مي دهيم
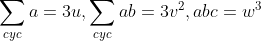 با خطي كردن نامساوي داريم:
با خطي كردن نامساوي داريم:



















 با كنار هم قرار دادن اين اتحاد ها مي توانيم نامساوي را به ازاي
با كنار هم قرار دادن اين اتحاد ها مي توانيم نامساوي را به ازاي
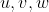 بنويسيم. پس با استفاده از
بنويسيم. پس با استفاده از
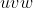 كافي است نامساوي را به ازاي
كافي است نامساوي را به ازاي
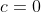 ثابت كنيم. با كمي ساده سازي داريم:
ثابت كنيم. با كمي ساده سازي داريم:
 حالا با استفاده از نامساوي هاي
حالا با استفاده از نامساوي هاي
 كه با نامساوي حسابي هندسي قابل اثباتند حكم ثابت مي شود.
كه با نامساوي حسابي هندسي قابل اثباتند حكم ثابت مي شود.
ديگه سعي كردم كامل بنويسم :4:.
تا آخر هفته راجع به راه حل ها اظهار نظری نمی کنم ولی لطفا راه حل ها را مرتب و با استدلال دقیق بنویس.
من راه حلت رو فهمیدم ولی این مدل نوشتن توی مرحله دوم باعث میشه ازت نمره کم کنن یعنی اگه دو تا گام رو یه گام بنویسی نمره اون گامی که بدیهی فرض کردی رو ازت کم می کنن
مثلا یه راه حل کامل رو با این مدل نوشتن از 7 نمره میدن 4 یا 5
اینو واسه همه گفتم نه فقط شما دوست عزیز
من راه حلت رو فهمیدم ولی این مدل نوشتن توی مرحله دوم باعث میشه ازت نمره کم کنن یعنی اگه دو تا گام رو یه گام بنویسی نمره اون گامی که بدیهی فرض کردی رو ازت کم می کنن
مثلا یه راه حل کامل رو با این مدل نوشتن از 7 نمره میدن 4 یا 5
اینو واسه همه گفتم نه فقط شما دوست عزیز
3- سوال خیلی قشنگی بود.
رابطه ی
---- دو نوشته به هم متصل شده است ----
٥- قرار مي دهيم
حال اتحاد هاي زير را در نظر بگيريد:


ديگه سعي كردم كامل بنويسم :4:.
