.::ماراتن دیفرانسیل::.
پاسخ : .::ماراتن دیفرانسیل::.
سوال بعدی.
حد مقابل. حساب کنید :

فوق العاده قشنگ بود.
من با استقرا جواب زیر رو بدست آوردم.
نکته ش اینه که توی هوپیتال گیری ها از مشتق سینوس در بقیه کسینوس ها استفاده کنیم و بقیه همه صفر هستند((خیلی فکر کنم بد گفتم!!!))
الان وقت نمی کنم راه حل بذارم.بعدا حتما میذارم
(2n+1)}{12})
فکر کنم اشتباهه.دوستان اگه لطف کنند ممنون میشم!
سوال بعدی.
حد مقابل. حساب کنید :
من با استقرا جواب زیر رو بدست آوردم.
نکته ش اینه که توی هوپیتال گیری ها از مشتق سینوس در بقیه کسینوس ها استفاده کنیم و بقیه همه صفر هستند((خیلی فکر کنم بد گفتم!!!))
الان وقت نمی کنم راه حل بذارم.بعدا حتما میذارم
فکر کنم اشتباهه.دوستان اگه لطف کنند ممنون میشم!
آخرین ویرایش توسط مدیر
- ارسال ها
- 327
- لایک ها
- 378
- امتیاز
- 0
پاسخ : .::ماراتن دیفرانسیل::.
سوال بعدی.
حد مقابل. حساب کنید :

ابتدا با استقرا ثابت میکنیم که:
\cos(2x)..\cos(nx)}{\mathrm{d^2}%20x}=-\frac{n(n+1)(2n+1)}{6})
=\cos(x)\cos(2x)...\cos(nx)\:,\:g(x)=\cos((n+1)x))
\cos(2x)..\cos(nx).\cos((n+1)x)}{\mathrm{d^2}%20x}=\lim_{x\to%200}\frac{\mathrm{d^2}%20f(x).g(x)}{\mathrm{d^2}%20x}=\lim_{x\to%200}(f''(x)g(x)+2f'(x)g'(x)+f(x)g''(x))=\lim_{x\to%200}(f''(x)g(x)+f(x)g''(x))=\lim_{x\to%200}f''(x)g(x)+\lim_{x\to%200}f(x)g''(x)=\lim_{x\to%200}-\frac{n(n+1)(2n+1)\cos((n+1)x)}{6}+\lim_{x\to%200}\cos(x)\cos(2x)...\cos(nx)(%20-(n+1)^2%20\cos((n+1)%20x))=-(\frac{n(n+1)(2n+1)}{6}+(n+1)^2)=-\frac{(n+1)(n+2)(2n+3)}{6})
\cos(2x)...\cos(nx)}{x^2}=\lim_{x\to%200}\frac{[1-\cos(x)\cos(2x)...\cos(nx)]'}{[x^2]'}=\lim_{x\to%200}\frac{-[\cos(x)\cos(2x)...\cos(nx)]'}{2x}=\lim_{x\to%200}\frac{-[\cos(x)\cos(2x)...\cos(nx)]''}{[2x]'}=\boxed{\frac{n(n+1)(2n+1)}{12}})
سوال بعدی.
حد مقابل. حساب کنید :
حکم واسه n=1,2 درسته. فرض میکنیم واسه n درسته و میخوایم واسه n+1 ثابتش کنیم:
پس حکم ثابت شد.
حالا حکم رو ثابت میکنیم:
حالا حکم رو ثابت میکنیم:
برای دومین بار هوپیتال زدن از این نکته استفاده کردیم که میدونیم توی صورت همشون sin.cos هست پس صفره، مخرجم که صفره. پس حله دیگه :4:
آخرین ویرایش توسط مدیر
پاسخ : .::ماراتن دیفرانسیل::.
ممنون از شما
خط آخر اثبات حکم استقرا رو یه توضیح کوچول موچول میدی؟؟؟یه ذره گیج شدم
ابتدا با استقرا ثابت میکنیم که:
\cos(2x)..\cos(nx)}{\mathrm{d^2}%20x}=-\frac{n(n+1)(2n+1)}{6})
=\cos(x)\cos(2x)...\cos(nx)\:,\:g(x)=\cos((n+1)x))
\cos(2x)..\cos(nx).\cos((n+1)x)}{\mathrm{d^2}%20x}=\lim_{x\to%200}\frac{\mathrm{d^2}%20f(x).g(x)}{\mathrm{d^2}%20x}=\lim_{x\to%200}(f''(x)g(x)+2f'(x)g'(x)+f(x)g''(x))=\lim_{x\to%200}(f''(x)g(x)+f(x)g''(x))=\lim_{x\to%200}f''(x)g(x)+\lim_{x\to%200}f(x)g''(x)=\lim_{x\to%200}-\frac{n(n+1)(2n+1)\cos((n+1)x)}{6}+\lim_{x\to%200}\cos(x)\cos(2x)...\cos(nx)(%20-(n+1)^2%20\cos((n+1)%20x))=-(\frac{n(n+1)(2n+1)\cos((n+1)x)}{6}+(n+1)^2)=-\frac{(n+1)(n+2)(2n+3)}{6})
\cos(2x)...\cos(nx)}{x^2}=\lim_{x\to%200}\frac{[1-\cos(x)\cos(2x)...\cos(nx)]'}{[x^2]'}=\lim_{x\to%200}\frac{-[\cos(x)\cos(2x)...\cos(nx)]'}{2x}=\lim_{x\to%200}\frac{-[\cos(x)\cos(2x)...\cos(nx)]''}{[2x]'}=\boxed{\frac{n(n+1)(2n+1)}{12}})
حکم واسه n=1,2 درسته. فرض میکنیم واسه n درسته و میخوایم واسه n+1 ثابتش کنیم:
پس حکم ثابت شد.
حالا حکم رو ثابت میکنیم:
حالا حکم رو ثابت میکنیم:
برای دومین بار هوپیتال زدن از این نکته استفاده کردیم که میدونیم توی صورت همشون sin.cos هست پس صفره، مخرجم که صفره. پس حله دیگه :4:
خط آخر اثبات حکم استقرا رو یه توضیح کوچول موچول میدی؟؟؟یه ذره گیج شدم
- ارسال ها
- 327
- لایک ها
- 378
- امتیاز
- 0
پاسخ : .::ماراتن دیفرانسیل::.
خواهش میکنم :1:
فقط از این نکته استفاده شد که
(2n+1)}{6}) . جای n بذارین n+1 . البته میتونین دو طرف رو هم بسط بدین. اینجوری:
. جای n بذارین n+1 . البته میتونین دو طرف رو هم بسط بدین. اینجوری:
(\frac{n(n+1)(2n+1)}{6}+(n+1)^2)-(\frac{(n+1)(n+2)(2n+3)}{6}) - Wolfram|Alpha
ممنون از شما
خط آخر اثبات حکم استقرا رو یه توضیح کوچول موچول میدی؟؟؟یه ذره گیج شدم
خط آخر اثبات حکم استقرا رو یه توضیح کوچول موچول میدی؟؟؟یه ذره گیج شدم
فقط از این نکته استفاده شد که
(\frac{n(n+1)(2n+1)}{6}+(n+1)^2)-(\frac{(n+1)(n+2)(2n+3)}{6}) - Wolfram|Alpha
- ارسال ها
- 327
- لایک ها
- 378
- امتیاز
- 0
پاسخ : .::ماراتن دیفرانسیل::.
از هر نقطه
 به نقطه متناظرش
به نقطه متناظرش
 وصل میکنیم. شیب خط گذرنده از نقطه
وصل میکنیم. شیب خط گذرنده از نقطه
 را
را
) بنامید.واضح است که تابع
بنامید.واضح است که تابع
) در بازه
در بازه
 پیوسته است.
پیوسته است.
برهان خلف: فرض کنید
\neq%20f(x+\frac{1}{2})\Leftrightarrow%20L(x)\neq%200) .
.
بدون کم شدن از کلیت مساله فرض کنید
%3E0) . حال اگر
. حال اگر
%3C0) آنگاه طبق قضیه مقدار میانگین
آنگاه طبق قضیه مقدار میانگین
\text{%20s.t.%20}L(y)=0) . پس در این حالت
. پس در این حالت
%3E0\implies%20f(1)%3Ef(\frac{1}{2})%3Ef(0))
سوال بعدی.
فرض کنید f تابعی پیوسته روی
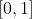 باشد به طوری که
باشد به طوری که
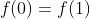 .ثابت کنید::
.ثابت کنید::

فرض کنید f تابعی پیوسته روی
برهان خلف: فرض کنید
بدون کم شدن از کلیت مساله فرض کنید
که تناقضه. حالت
%3C0) هم به طور مشابه رد میشه. پس حکم ثابت شد :1:
هم به طور مشابه رد میشه. پس حکم ثابت شد :1:
آخرین ویرایش توسط مدیر

