ماراتن هندسه version 2

S

shoki

New Member
#1
ارسال ها
637
لایک ها
128
امتیاز
0
#1
khob gofte budam ye marathon hendeseye dige baz mikonam
tebghe mamul in ham ghavaninesh ....
hich gune matlabi ke rabti be in topic nadare matrah nakonid .
ebteda javab midid bad masaleye jadid tarh mikonid .
sorry for the tone ....
khob...
let's start ...
soale aval :
in soal dar ketabe khoshkhan hast ....
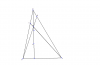
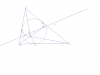
dar mosalase ABC khate delkhahe d az O ke markaze dayereye mohitiye ABC ast
migozarad va AB va AC ra dar C' va B' ghat mikonad .hal sabet konid ke do dayereye be ghotre BB' va CC' ham digar ra
ruye (O) va ruye (N) ghat mikonand (N markaze dayereye noh noghteye ABC hast )
good luck ....

Edit :
yadam raft begam ke agar ham soali az khode shakhs dashtid (masalan in ke chejuri sheklha ro mikeshid ya in ke chejuri ba LaTeX minevisid (ebarate riazi ro migam ) bayad be khode shakhs peyghame shakhsi beferestid va ya har juri digei ke deletun khast faghat in ke inja matrah nakonin ).
.ba tashakore faravan
 
A

Aref

New Member
#2
ارسال ها
1,262
لایک ها
1,008
امتیاز
0
#2
shoki می نویسد:

خب گفته بودم یه ماراتن هندسه ی دیگه باز می کنم
طبق معمول این هم قوانینش....
هیچ گونه مطلبی که ربطی به این تاپیک نداره مطرح نکنید
ابتدا جواب میدید بعد مسئله ی جدید طرح می کنید.
ببخشید به خاطر لحن صحبت....
خب....
بیایید شروع کنیم....
سوال اول:
این سوال در کتاب خوشخوان هست....
در مثلث ABC خط دلخواه d از O که مرکز دایره ی محیطی مثلث ABC است می گذرد و خطوط AB و AC را به ترتیب در 'C و 'B قطع می کند. حال ثابت کنید که دو دایره ی به قطر 'BB و 'CC همدیگر را در (O) و (N) قطع می کنند.(N مرکز دایره ی نه نقطه ی مثلث ABC است.)
موفق باشید....

پی نوشت:
یادم رفت بگم که اگر سوالی از کسی داشتید(مثلا این که چجوری شکل رسم می کنید یا عبارت های ریاضی رو می نویسید) باید به خود فرد پیغام شخصی بفرستید یا هر جور دیگه ای که دلتون میخواد فقط این جا مطرح نکنید.
با تشکر فراوان
لطفا فارسی بنویسید!
 
seifi_seifi

seifi_seifi

New Member
#5
ارسال ها
335
لایک ها
8
امتیاز
0
#5
ابتدا نام 'C و 'B را تغییر میدهیم به C[SUB]1[/SUB] و B[SUB]1[/SUB] (برای راحتی نوشتن) و فرض کنید M دومین B[SUB]1[/SUB]B[SUB]2[/SUB] با دایره محیطی ABC میگیریم.

B[SUB]2[/SUB] و C[SUB]2[/SUB] را نقاط مقابل قطری B و C مینامیم.طبق پاسکال برای شش ضلعی AB[SUB]2[/SUB]CMBC[SUB]2[/SUB] بدست میاید O و B[SUB]1[/SUB] و C'[SUB]1[/SUB] روی یک خطند.

پس C'[SUB]1[/SUB] بر C[SUB]1[/SUB] منطبق است و چون BMB[SUB]2[/SUB]=BMB[SUB]1[/SUB]=CMC[SUB]2[/SUB]=CMC[SUB]1[/SUB]=90 پس M همان محل برخورد دو دایره است.

برای قسمت بعدی دو لم مطرح میکنیم :

لم1:اگر M,N دو نقطه روی AB,AC باشند آنگاه وتر مشترک دو دایره به قطرهای BN ,CM از H میگذرد.(اثباتش سخت نیست و فکر کنم تو

شارگین هم اثباتش باشه.)

لم 2 : اگر در مثلث ABC داشته باشیم AA[SUB]1[/SUB] ارتفاع و H مرکز ارتفاعی باشد و P نقطه ای دلخواه از دایره ی محیطی مثلث ABC باشد و

M نقطه ای بر خط HP باشد که HP.HM=HA[SUB]1[/SUB].HA آنگاه M روی دایره ی نه نقطه است.(این رو هم فکر کنم تو کتاب آقا احمدپور

یا شارگین دیدم)

حال اگر N را نقطه ی برخورد دوم دو دایره بگیریم آنگاه H روی MN قرار دارد و اگر BB[SUB]0[/SUB] ارتفاع باشد داریم MH.HN=BH.HB[SUB]0[/SUB] پس N روی دایره

نه نقطه قرار دارد.

(سوال سنگینی بود. پارسال اینو آقا احمدپور سر کلاس دادند قسمت اولش حل شد ولی قسمت دومش حل نشد بعد آقا احمدپور این دوتا

لم رو گفتند و حل شد.)
 
S

shoki

New Member
#6
ارسال ها
637
لایک ها
128
امتیاز
0
#6
احسنت عالی‌ بود ولی‌ یه راه حل دیگری‌ هم هست ...
برای راهنمایی‌ میتونید به صفحهٔ ۱۳۴ کتاب خوشخوان رجوع کنید ..
 
seifi_seifi

seifi_seifi

New Member
#7
ارسال ها
335
لایک ها
8
امتیاز
0
#7
سوال بعدی :

در مثلث ABC داریم H مرکز ارتفاعی و H[SUB]1[/SUB] قرینه ی H نسبت به A میباشد. محل برخورد H[SUB]1[/SUB]C وAB را M و محل برخورد H[SUB]1[/SUB]B با AC را N مینامیم.

ثابت کنید BM=CN اگر و فقط اگر A=60

من این سوال رو فکر کنم 1 یا 2 ماه پیش تو mathlinks دیدم و خودم حلش کردم ولی با محاسبات زیاد و تو mathlinksکسی حل نکرده بود.

و دنبال راه حل هندسیش هستم.
 

پیوست ها

S

shoki

New Member
#8
ارسال ها
637
لایک ها
128
امتیاز
0
#8
این سوال به راحتی‌ با منلا ئوس قابل حله ولی‌ یه مقداری زشت می‌شه...
من هم دنبال راه حال قشنگش دارم می‌گردم ....
 
seifi_seifi

seifi_seifi

New Member
#9
ارسال ها
335
لایک ها
8
امتیاز
0
#9
اگه راه حل قشنگ هندسی داشتی حتما بذار. ممنون.
 
S

shoki

New Member
#10
ارسال ها
637
لایک ها
128
امتیاز
0
#10
baraye in ke topic nakhabe majburam soale badi ro bezaram:
rasti baraye soale ghabli ham mitunid az menelaus berid va ham az mokhtasate (x,y) va agar kasi ham rahe hale ba mokhtasate (x,y) ro ehayanan nemidune chiye hatman beporse ....
khob soale badi :
tamime ghaziyey ceva ra esbat konid :
[center:6594792de1]
فرض کنید که n یک عدد صحیح مثبت باشد و
یک ۲n+۱ ضلعی دلخواه باشد (مثلا میتونه مقعر باشه ). در ادامه با اندیس های دوری به مد ۲n+۱ کار می‌کنیم به طوری که
برای‌ هر i. فرض کنید که P نقطه در صفحه باشد؛ برای هر i، فرض کنید که
خط
را در نقطه ی
قطع می‌کند . ثابت کنید که​
[/center:6594792de1]
[center:6594792de1]
[/center:6594792de1]
 
S

shoki

New Member
#11
ارسال ها
637
لایک ها
128
امتیاز
0
#11
بابا این که خیلی راحته...
من از شما راه حل کامل نمی خام حتی اگر شیوه ی کار رو بگید حله....
اگه تا ساعت 8 امشب کسی حل رو نذاره جواب رو میذارم...
 
S

shoki

New Member
#13
ارسال ها
637
لایک ها
128
امتیاز
0
#13
خوب مجبورم شیوه کار رو بگم ...
لم ؟فرض کنید که در
داشته باشیم
آنگاه داریم

.

حالا تمامی این روابط رو برای هر
بنویسید و در هم ضرب کنید...
سوال بعدی ...
در مثلث
مرکز دایره ی محاطی داخلی
می باشد و در نقاط
بر اضلاع مماس می باشد .فرض کنید که خط
از
بگذرد و نقاط
عمود های
بر
باشند آنگاه ثابت شود
همرسند.​
 

پیوست ها

Olympiad

Olympiad

New Member
#14
ارسال ها
1,268
لایک ها
134
امتیاز
0
#14
سلام به دوستان .
سوال 4
البته با اجازه ي دوستان
H1,H2,H3 پاي ارتفاع هاي مثلثي دلخواه هستند . و زاويه هاي A1=B1=C1 ميباشند .
ثابت كنيد HX=HY=HZ
 
mahanmath

mahanmath

New Member
#16
ارسال ها
898
لایک ها
701
امتیاز
0
#16
سواله 4

Kafie sabet konim HXY motasaviolsaghein hast.
baraye in kar sabet mikonim HXY=HYX (zavie) hast.
HXBC va , AHXC va ABH_1H_3 mohatiand (esbateshoon asoone faghat zavias) pas berahati tasvie do zavie ye HXY va HYX bedast miad.

Rasti soale shoki hast man dige nemizaram.
 
Olympiad

Olympiad

New Member
#17
ارسال ها
1,268
لایک ها
134
امتیاز
0
#17
mmath گفت
سواله 4

Kafie sabet konim HXY motasaviolsaghein hast.
baraye in kar sabet mikonim HXY=HYX (zavie) hast.
HXBC va , AHXC va ABH_1H_3 mohatiand (esbateshoon asoone faghat zavias) pas berahati tasvie do zavie ye HXY va HYX bedast miad.

Rasti soale shoki hast man dige nemizaram.
کلیک کنید تا باز شود...
اصلا با زاويه نوشتن حل نميشه
 
mahanmath

mahanmath

New Member
#19
ارسال ها
898
لایک ها
701
امتیاز
0
#19
Olympiad گفت
mmath گفت
سواله 4

Kafie sabet konim HXY motasaviolsaghein hast.
baraye in kar sabet mikonim HXY=HYX (zavie) hast.
HXBC va , AHXC va ABH_1H_3 mohatiand (esbateshoon asoone faghat zavias) pas berahati tasavie do zavie ye HXY va HYX bedast miad.

Rasti soale shoki hast man dige nemizaram.
کلیک کنید تا باز شود...
اصلا با زاويه نوشتن حل نميشه
کلیک کنید تا باز شود...

B[SUB]1[/SUB]=C[SUB]1[/SUB] pas BXHC mohati.
C[SUB]1[/SUB]=A[SUB]1[/SUB] pas AHYC mohati
BH[SUB]3[/SUB] va AH[SUB]1[/SUB] ertefa hastan pas ,ABH[SUB]1[/SUB]H[SUB]3[/SUB] mohati
HBC = HAC
HAC=HYX zavie kharegi
HXBC mohati HXC = HBC


Pas HXY =HYX
Pas HX=HY
 
برای ارسال پاسخ شما باید وارد سیستم شوید.
بالا