ماراتن هندسه version 2

[seifi_seifi]

ابن سوال= سوال 134 شارگین برید اون جا جوابشو بخونید.

البته تا سوال آقای shoki حل نشده سوال نذارید.(قانون تاپیکه.)

 

[Fardad]

کتاب شاریگین رو از کجا می تونم دانلود کنم یا بخرم .
اگه لینکش ذاشه ممنونم .

 

[seifi_seifi]

نمیدونم فکر نمیکنم دیگه چاپ بشه.

من هم تا حالا تو اینترنت ندیدم.ولی اکثر کتابخانه ها دارند.

 

[Olympiad]

فكر نكنم چاپ متوقف شده باشه

 

[danialm]

من که چند وقت پیش خریدم

 

[Olympiad]

من که چند وقت پیش خریدم

كي خريدي‌‌؟‌؟؟‌؟‌؟‌ بهمن درختي‌؟؟؟

 

[danialm]

اره سال پیش از همون جا خریدم

 

[shoki]

خوب از اون جایی که سوال به هپروت رفت دوباره آپش می کنم ... یعنی واقعا سوالم این قدر زشته که کسی حل نمی کنه ؟؟

در مثلث

مرکز دایره ی محاطی داخلی

می باشد و در نقاط

بر اضلاع

مماس می باشد .فرض کنید که خط

از

بگذرد و

نقاط عمود های

بر

باشند آنگاه ثابت شود

همرسند.

 

[shoki]

تا یک ساعت دیگه یه راهنمایی و تا سه ساعت دیگه حل رو می فرستم ...

 

[majidgoodarzi]

فرض کنید DD-1 دایره را در D-3 قطع کند.DD_1,FF_1,EE_1 در بی نهایت همرس اند پس AD_3,BE_3,CF_3 همرس اند و می دانیم AD,BE,CF نیز همرس اند. پس میانه ها نیز همرس اند.اگه درسته سوال بعدی رو بدم؟

 

[shoki]

از اون جایی که چند وقته مسئله حل نکردم مخم فسیل شده ... می تونی آخرین قسمت رو بگی چه جوری نتیجه گرفتی : ''
پس میانه ها نیز همرس اند'' ؟؟

 

[majidgoodarzi]

فکر کنم کلا چرند نوشتم.لطفا تا فردا راه نمایی نکن.چون من تازه سوال رو دیدم و الان هم وقت ندارم.

 

[shoki]

ok

 

[majidgoodarzi]

حل نشد.راهنمایی کن.

 

[shoki]

قطب و قطبی نسبت به دایره ی محاطی + منلائوس ...

 

[majidgoodarzi]

لطفا حل را بگو.نمیتونم.

 

[shoki]

ابتدا سعی می کنیم که قطب

رو پیدا کنیم .
چون قطبی آن نقطه از A گذشته پس باید روی قطبی A باشه ... یعنی باید روی EF باشه ... از طرفی چون از

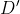گذشته پس باید روی قطبی این نقطه هم باشه ... اما قطبی

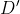در اصل چه خطیه ؟ خوب بدیهیه که نقطه ی برخورد BC با خط d در اصل روی قطبی

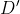قرارداره ( چون که D'D بر خطی که از I و

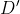می گذره عموده) . بنابریان اگه قرار بدیم :

اون وقت خط عود در نقطه ی

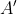بر d می شه قطبیه

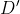و ما هم اسمشو می ذاریم :

. پس سرانجام می شه نتیجه گرفت که قطب

در اصل می شه :

. حالا باید ثابت کنیم که :

هم خطند . چون این سه نقطه روی اضلاع مثلث DEF هستند از منلائوس برای همین مثلث استفاده می کنیم . من در شکلی که گذاشتم مثلث DEF رو کاملا جدا گانه بررسی خواهم کرد و دیگه کاری هم به ABC نخواهم داشت ...
همون طور که در شکل ملاحظه می کنید داریم

چرا که همگی بر خط d عمودند. حالا ما باید سعی کنیم که نسبت

رومحاسبه کنیم . اما به جاش می تونیم نسبت مساوی اونو یعنی :

رو محاسبه کنیم . حالا فرض کنید که شعاع دایره ی محاطی داخلی r باشه. از طرفی قرار بدید :

.
حالا می تونیم

رو جداگانه محاسبه کنیم : داریم :

دقت کنید که چون

مثلث قائم الزاویه هست و چون

ارتفاع اونه پس

.

حالا اگه به همین ترتیب

رو محاسبه کنیم و به همین ترتیب

رو محاسبه کنید و در هم ضرب کنید به راحتی می بینید که حاصلش می شه یک . پس حله ...

 

[shoki]

نمی دونم چرا نمی تونم شکل رو آپلودش کنم !!! برام می نویسه :


از سهميه آپلود خود استفاده کرده ايد 256 �ا عزض تاسف شما بيشتر از


به هر حال بدون شکل هم می شه فهمید ... البته امیدوارم که بفهمید

اگه توضیحی احتیاج داشت بگید ...

 

[shoki]

راستی توی شکلم

نسبت به I هم طرفند.

 

[majidgoodarzi]

عالی بود.حالا سوال بعد لطفا...