.::ماراتن گراف::.
پاسخ : ماراتون گراف
راه حل سوال 2 :
حکم رو به ازای هر تورنمنت n رأسی که تو شرایط مساله صدق میکنه ثابت میکنیم. ابتدا از استقراء استفاده میکنیم و فرض میکنیم به ازای مقادیر کمتر از n حکم صحیحه. (پای استقرای برای n=3 بدیهیه). اگر رأسی وجود داشته باشه که تمام یال هاش بهش وارد شده باشند یا ازش خارج شده باشند اون رأس رو حذف میکنیم. طبق فرض استقراء ، راسی وجود داره که اگه جهت تمام یال هاش رو برعکس کنیم گراف قویا همبند میشه. حالا اون رأس حذف شده رو اضافه میکنیم. میدونیم دقیقا جهت یکی از یال هاش تغییر کرده. پس از اون میتونیم به راسی دیگه وارد شیم. و از اون راس به هر راس دلخواه وارد شیم. همچنین میتونیم از هر راس دلخواه به اون بریم. پس در این حالت مساله حله. حالا فرض کنیم هر راس حداقل یک یال ورودی و حداقل یک یال خروجی داره. میدونیم توی هر تورنمنت دور هامیلتونی وجود داره. یعنی میتونیم راس ها رو مرتب بچینیم به طوری که از هر
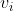به
بتونیم بریم. الان میدونیم بین راس اول و آخر
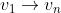. چون اگر از
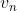به
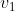یک مسیر به طول 1 وجود داشت خلاف فرض که گراف قویا همبند نیست میشد. (چون از هر راس میشد به هر راس دیگه رفت). حالا مسیر به طول یک بین
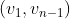رو در نظر بگیریم. اگر این مسیر به سمت
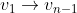بود با عوض کردن جهت تمام یال های
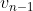به هدف میرسیم. چون اون وقت از
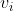(i<n-1) به
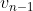میریم و از اون
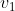و چون راسی وجود داره که جهتش به سمت
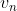هست از هر راسی به هر راس دیگه میتونیم بریم. اگر مسیر به طول یک بین
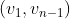به سمت
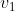بود با عوض کردن جهت یال های
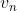به حکم مورد نظر میرسیم. (مشابه حالت قبل)
چون سوال « 1 » یه کمی سخته، اینم سوال دوّمی:
یک تورنمنت 100 راسی داده شده است. این تورنمنت قویا همبند نیست. ثابت کنید می توان جهت تمام یال های متصل به یک راس را عوض کرد طوری که تورنمنت حاصل قویا همبند باشد.
یک تورنمنت 100 راسی داده شده است. این تورنمنت قویا همبند نیست. ثابت کنید می توان جهت تمام یال های متصل به یک راس را عوض کرد طوری که تورنمنت حاصل قویا همبند باشد.
راه حل سوال 2 :
حکم رو به ازای هر تورنمنت n رأسی که تو شرایط مساله صدق میکنه ثابت میکنیم. ابتدا از استقراء استفاده میکنیم و فرض میکنیم به ازای مقادیر کمتر از n حکم صحیحه. (پای استقرای برای n=3 بدیهیه). اگر رأسی وجود داشته باشه که تمام یال هاش بهش وارد شده باشند یا ازش خارج شده باشند اون رأس رو حذف میکنیم. طبق فرض استقراء ، راسی وجود داره که اگه جهت تمام یال هاش رو برعکس کنیم گراف قویا همبند میشه. حالا اون رأس حذف شده رو اضافه میکنیم. میدونیم دقیقا جهت یکی از یال هاش تغییر کرده. پس از اون میتونیم به راسی دیگه وارد شیم. و از اون راس به هر راس دلخواه وارد شیم. همچنین میتونیم از هر راس دلخواه به اون بریم. پس در این حالت مساله حله. حالا فرض کنیم هر راس حداقل یک یال ورودی و حداقل یک یال خروجی داره. میدونیم توی هر تورنمنت دور هامیلتونی وجود داره. یعنی میتونیم راس ها رو مرتب بچینیم به طوری که از هر
پاسخ : ماراتون گراف
سوال 2:
نگاه کن. یه چیزی. بهتر نبود می گفتی که یه راسی رو حذف می کنیم که هم راس ورودی و هم راس خروجیش حداقل درجه اش 2 باشه ( همیشه همچین راسی وجود داره (چرا؟ ) ) وقتی اونو حذفش کنیم، طبق فرض استقرا یه راسی رو می تونیم یال هاش رو تغییر بدیم طوری که گراف قویا همبند بشه. و بعد از این که گراف تغییر یافت اون راس که در نظر گرفتیم هم درجه خروجی و هم درجه ورودیش حداقل یک هست. پس به راس v می ره و راس v هم می تونه به هر راسی بره و بیاد. دی
[HR][/HR]
علاوه بر این یه بار دیگه راهتو از اونجایی که گفتی اگه یه راسی نباشه که درجه ورودی یا خروجیش صفر باشه توضیح بده. ( یه کمی روون تر ) دی
سوال 2:
نگاه کن. یه چیزی. بهتر نبود می گفتی که یه راسی رو حذف می کنیم که هم راس ورودی و هم راس خروجیش حداقل درجه اش 2 باشه ( همیشه همچین راسی وجود داره (چرا؟ ) ) وقتی اونو حذفش کنیم، طبق فرض استقرا یه راسی رو می تونیم یال هاش رو تغییر بدیم طوری که گراف قویا همبند بشه. و بعد از این که گراف تغییر یافت اون راس که در نظر گرفتیم هم درجه خروجی و هم درجه ورودیش حداقل یک هست. پس به راس v می ره و راس v هم می تونه به هر راسی بره و بیاد. دی
[HR][/HR]
علاوه بر این یه بار دیگه راهتو از اونجایی که گفتی اگه یه راسی نباشه که درجه ورودی یا خروجیش صفر باشه توضیح بده. ( یه کمی روون تر ) دی
پاسخ : ماراتون گراف
بله حق با شماست. این راه کوتاه تره
توضیح که فقط حالت بندی کردم دیگه ! میدونیم بین هر دو رأس یک یال وجود داره. اول گفتم دور هامیلتونی داریم
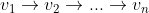. بعدش ادعا کردم اون یالی که بین v_1 و v_n هستش باید به سمت v_n باشه چون در غیر این صورت از هر v_i میشه به v_j رفت. حالا جهت یال بین v_1 و v_n-1 رو در نظر میگیریم. اگر به سمت v_1 باشه پس بین v_1 تا v_n-1 از هر راسی میشه به هر راسی رفت. حالا فقط کافیه جهت یال های v_n رو برعکس کنیم. اولا از v_1 میشه به v_n رفت. پس از هر راسی میشه به v_1 رفت و از اون به v_n. ثانیا از v_n به v_n-1 میشه رفت و از اون به هر راس دیگه . پس مساله حله !
اگر جهت v_1 و v_n-1 به سمت v_n-1 بود، جهت یال های v_n-1 رو برعکس میکنیم. پس از v_1 میشه به تمام v_2, v_3 , .... , v_n-1 رفت و از v_n-1 به v_1. i همچنین راسی وجود داره که به سمت v_n میره. پس از اون میشه به v_n رفت و از v_n هم به v_1 و .... تمام !
خب اینم یه راهه برای خودش دیگه :99:
بله حق با شماست. این راه کوتاه تره
توضیح که فقط حالت بندی کردم دیگه ! میدونیم بین هر دو رأس یک یال وجود داره. اول گفتم دور هامیلتونی داریم
اگر جهت v_1 و v_n-1 به سمت v_n-1 بود، جهت یال های v_n-1 رو برعکس میکنیم. پس از v_1 میشه به تمام v_2, v_3 , .... , v_n-1 رفت و از v_n-1 به v_1. i همچنین راسی وجود داره که به سمت v_n میره. پس از اون میشه به v_n رفت و از v_n هم به v_1 و .... تمام !
خب اینم یه راهه برای خودش دیگه :99:
پاسخ : ماراتون گراف
پاسخ سوال 3:
یال هایی که به راس های 1 تا k وصل هستند را به دو دسته تقسیم می کنیم:
یال های داخلی: یال هایی که فقط بین راس های 1 تا k هستند.
یال های خارجی: یال هایی که بین راس های « 1 تا k » و « k+1 تا n » هستند.
حداکثر تعداد یال های داخلی برابر
)
هست.
از طرفی از (i=k+1 to n) اگر
\leqslant&space;k)
حداکثر
)
یال خارجی از
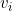به رووس 1 تا k وصل شده. و اگر
>&space;k)
حداکثر k تا از
به رووس 1 تا k وصل است. ( گراف ساده است. )
پاسخ سوال 3:
یال هایی که به راس های 1 تا k وصل هستند را به دو دسته تقسیم می کنیم:
یال های داخلی: یال هایی که فقط بین راس های 1 تا k هستند.
یال های خارجی: یال هایی که بین راس های « 1 تا k » و « k+1 تا n » هستند.
حداکثر تعداد یال های داخلی برابر
از طرفی از (i=k+1 to n) اگر
پاسخ : ماراتون گراف
خب،استقرا زدی؟واسه حکم باید یه جور خوب رنگ امیزی کنی دیگه.پس سعی کن یه جورایی بین یالهای مجاور و غیر مجاور این کار رو انجام بدی.این سوال،سواله اسونی نیست،همچنین سوال خوبی محسوب میشه،پس هر چقدر روش فک کنی ضرر نمی کنی!حالا اگه خواستی امشب یا فردا جواب کامل رو قرار میدم!(البته با اجازه گودرز!)
خب،استقرا زدی؟واسه حکم باید یه جور خوب رنگ امیزی کنی دیگه.پس سعی کن یه جورایی بین یالهای مجاور و غیر مجاور این کار رو انجام بدی.این سوال،سواله اسونی نیست،همچنین سوال خوبی محسوب میشه،پس هر چقدر روش فک کنی ضرر نمی کنی!حالا اگه خواستی امشب یا فردا جواب کامل رو قرار میدم!(البته با اجازه گودرز!)