مساحت بزرگترین مربع
راه حل سوالی که خودم گذاشتمو نمی دونم
ولی خوب تا مساله ی شما رو دیدم یاد این سوال افتادم ... در واقع یه بار دیدم پدرام فر و تفاق دارن رو این سوال(در حالت مکعب و نه مکعب مسطیل) فکر می کنن ... حالا نمی دونم به نتیجه رسیدند یا نه! ثانیا شرمنده اگه جای این سوال این جا نیست... ولی خودم می خوام روش فکر کنم
ببینم چی می شه
shoki گفت
راه حل سوالی که خودم گذاشتمو نمی دونم
ولی خوب تا مساله ی شما رو دیدم یاد این سوال افتادم ... در واقع یه بار دیدم پدرام فر و تفاق دارن رو این سوال(در حالت مکعب و نه مکعب مسطیل) فکر می کنن ... حالا نمی دونم به نتیجه رسیدند یا نه! ثانیا شرمنده اگه جای این سوال این جا نیست... ولی خودم می خوام روش فکر کنم
ببینم چی می شه
سوال خودم که تبدیل به این مسئله ی جبری میشه(قابل پیش بینی بود که این طور باشه ) :
فرض کنید که دایره ی با مرکز
که در آن
با شعاع r و با صفحه ی عمود بر بردار
دایره ی با آن خاصیت باشد . در آن صورت باید توجه داشت که معادله ی آن دایره عبارت خواهد بود از :
[center:7cf4a71025]
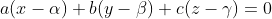
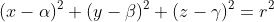
فرض کنید که دایره ی با مرکز
[center:7cf4a71025]
حالا ما باید درصدد پیدا کردن
باشیم...
این فعلا اون چیزی هس که در مورد مسئله ی اضافی می شه گفت. در مورد مسئله ی شما هم :
[/center:7cf4a71025]این فعلا اون چیزی هس که در مورد مسئله ی اضافی می شه گفت. در مورد مسئله ی شما هم :
اگر مربعی که یکی از اضلاعش تماما بر روی BC است را در نظر بگیرید طول ضلعش می شود :
. و به همین ترتیب برای باقیه مربع ها. حالا باید دید که برای کدام مثلث مجموع ارتفاع و ضلع مینیمم است. چون حاصلضرب ثابت است پس تساوی در حالت تساوی ارتفاع و ضلع وارد بر آن اتفاق می افتد. یعنی زمانی که هر دوی آن ها
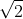هستند. حالا مساحت مربع هم به راحتی به دست میاد.
یادم رفت بگم که توی پست قبلی رئوس مکعب دارای اضلاع واقع بر محور ها بوده و مختص های رئوس مکعب نامنفی است.
یه راهی براش پیدا کردم که به نتیجه می رسه ولی خیلی خر کاری داره ... تصویر کردن یک دایره بر یک صفحه یک بیضی رو نتیجه می ده که قطر بزرگ اون بیضی همون قطر دایره است. با استفاده از این نکته به این نتیجه می رسیم که با تصویر کردن دایره ی مطلوب بر صفحه ی z=0 باید یک بیضی درون وجه واقع بر صفحه ی z=0 به وجود بیاد که دارای خواص زیر است :
1- نصف قطر بزرگش a بوده(=شعاع خود دایره) و نصف کوچکترین قطرش b بوده که در آن
(چرا؟).
2-کل بیضی درون یا روی مماس بر اضلاع وجه است.
3-a بزرگترین مقدار بین تمامی بیضی های با خاصیت 1 و2 است.
یعنی عملا مسئله به یه مسئله در دو بعد تبدیل می شه که حالا این a رو می شه با مقدار زیادی محاسبات و مشتق و غیره بدست آورد ... ولی دنبال راه آدم وار تر هم هستم تا بتونم اون بیضی رو پیدا کنم ... برای پیدا کردنش فکر کنم لازم باشه یه سری اطلاعات در مورد بیضی های محاطی جمع آوری کنم تا ببینم چی می شه ... ولی نمی دونم چرا احساس می کنم راه سوال خیلی راحت تر باشه
... که اگر واقعا این طور باشه که اونوقت دیگه
...
یه راهی براش پیدا کردم که به نتیجه می رسه ولی خیلی خر کاری داره ... تصویر کردن یک دایره بر یک صفحه یک بیضی رو نتیجه می ده که قطر بزرگ اون بیضی همون قطر دایره است. با استفاده از این نکته به این نتیجه می رسیم که با تصویر کردن دایره ی مطلوب بر صفحه ی z=0 باید یک بیضی درون وجه واقع بر صفحه ی z=0 به وجود بیاد که دارای خواص زیر است :
1- نصف قطر بزرگش a بوده(=شعاع خود دایره) و نصف کوچکترین قطرش b بوده که در آن
2-کل بیضی درون یا روی مماس بر اضلاع وجه است.
3-a بزرگترین مقدار بین تمامی بیضی های با خاصیت 1 و2 است.
یعنی عملا مسئله به یه مسئله در دو بعد تبدیل می شه که حالا این a رو می شه با مقدار زیادی محاسبات و مشتق و غیره بدست آورد ... ولی دنبال راه آدم وار تر هم هستم تا بتونم اون بیضی رو پیدا کنم ... برای پیدا کردنش فکر کنم لازم باشه یه سری اطلاعات در مورد بیضی های محاطی جمع آوری کنم تا ببینم چی می شه ... ولی نمی دونم چرا احساس می کنم راه سوال خیلی راحت تر باشه
shoki گفت
راه حل سوالی که خودم گذاشتمو نمی دونم
ولی خوب تا مساله ی شما رو دیدم یاد این سوال افتادم ... در واقع یه بار دیدم پدرام فر و تفاق دارن رو این سوال(در حالت مکعب و نه مکعب مسطیل) فکر می کنن ... حالا نمی دونم به نتیجه رسیدند یا نه! ثانیا شرمنده اگه جای این سوال این جا نیست... ولی خودم می خوام روش فکر کنم
ببینم چی می شه
