معادلات تابعی
پاسخ : معادلات تابعی
می توان گفت از آنجایی که دامنه ی ما تمامی اعدادحقیقی می باشند تابع مورد نظر ما بایستی اکیدا یکنوا باشد چرا که در غیر این صورت وجود خواهدداشت
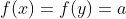وخواهیم داشت:
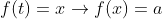
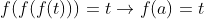
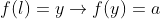
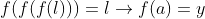
که در این صورت شرط تابع بودن نقض می شود پس تابع ما اکیدا یکنوا بوده و دو حالت خواهیم داشت:
1-تابع اکیدا نزولی: اگر تابع ما اکیدا نزولی باشد آنگاه
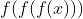نیز اکیدا نزولی خواهد بود پس بایستی
اما می دانیم چنین شرایطی در مجموعه اعدادحقیقی همیشه برقرارنیست و وجود دارد
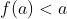(چون اکیدا نزولی است.)
2-تابع اکیدا صعودی:
1)اگر آنگاه واین حالت رد می شود.
2) اگر
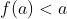آنگاه
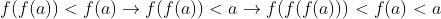
که این حالت هم رد می شود.
3) و تنها حالت
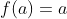باقی می ماند که در شرایط مساله صدق کرده و پاسخ سوال تابع همانی(نیم سازربع اول وسوم می باشد.)
می توان گفت از آنجایی که دامنه ی ما تمامی اعدادحقیقی می باشند تابع مورد نظر ما بایستی اکیدا یکنوا باشد چرا که در غیر این صورت وجود خواهدداشت
که در این صورت شرط تابع بودن نقض می شود پس تابع ما اکیدا یکنوا بوده و دو حالت خواهیم داشت:
1-تابع اکیدا نزولی: اگر تابع ما اکیدا نزولی باشد آنگاه
اما می دانیم چنین شرایطی در مجموعه اعدادحقیقی همیشه برقرارنیست و وجود دارد
2-تابع اکیدا صعودی:
1)اگر آنگاه واین حالت رد می شود.
2) اگر
که این حالت هم رد می شود.
3) و تنها حالت
- ارسال ها
- 159
- لایک ها
- 282
- امتیاز
- 0
پاسخ : معادلات تابعی
این که اکیدا یکنوایی نیست یک به یکی است!
این تابع بی نهایت جواب دارد. جوابهایی که برخی خیلی زیبا هم نیستند. برای مثال
می توان گفت از آنجایی که دامنه ی ما تمامی اعدادحقیقی می باشند تابع مورد نظر ما بایستی اکیدا یکنوا باشد چرا که در غیر این صورت وجود خواهدداشت
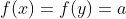وخواهیم داشت:
این تابع بی نهایت جواب دارد. جوابهایی که برخی خیلی زیبا هم نیستند. برای مثال
آخرین ویرایش توسط مدیر
پاسخ : معادلات تابعی
بله اون توضیحاتی رو که من نوشتم تمامی توابع پیوسته رو مورد بررسی قرار میده (که درست ضعف کار هم همین جاست) در حالی که می توان تابع مورد نظر خود را همون طور که آقای TheOverlord عرض کردند مجموعه ای از زوج های مرتب دانست
بله اون توضیحاتی رو که من نوشتم تمامی توابع پیوسته رو مورد بررسی قرار میده (که درست ضعف کار هم همین جاست) در حالی که می توان تابع مورد نظر خود را همون طور که آقای TheOverlord عرض کردند مجموعه ای از زوج های مرتب دانست