معادله ای در اعداد گویا .....
- ارسال ها
- 327
- لایک ها
- 378
- امتیاز
- 0
پاسخ : معادله ای در اعداد گویا .....
^2+(y+1.5)^2+(z+1.5)^2=1.75)

حال سه حالت را در نظر میگیریم:
حالت اول) اگر هر سه این اعداد ناصفر باشند،آنگاه کوچکترین مضرب مشترک مخرج این سه عدد را
 فرض میکنیم.حال مینویسیم:
فرض میکنیم.حال مینویسیم:
=d^2\Rightarrow 7|d\Rightarrow d=7s\Rightarrow u^2+v^2=7s^2)
با کمی ساده سازی داریم:
حال از سه تغییر متغیر
\\ b=2(y+1.5)\\ c=2(z+1.5) \end{matrix}\right.) استفاده کرده و معادله به معادله زیر تبدیل می شود:
استفاده کرده و معادله به معادله زیر تبدیل می شود:
حال سه حالت را در نظر میگیریم:
حالت اول) اگر هر سه این اعداد ناصفر باشند،آنگاه کوچکترین مضرب مشترک مخرج این سه عدد را
(
 ,
,
=1) )
)


)
از آنجا که
=1) است و تنها حالت های ممکن برای یک عدد صحیح مربع کامل در مبنای 8،اعداد 0و1و4 هستند، در می یابیم که هیچ حالتی وجود ندارد.:3: پس این حالت نقض شد.
است و تنها حالت های ممکن برای یک عدد صحیح مربع کامل در مبنای 8،اعداد 0و1و4 هستند، در می یابیم که هیچ حالتی وجود ندارد.:3: پس این حالت نقض شد.
حالت دوم) حال اگر یکی از این اعداد مثلا a صفر باشد آنگاه به معادله
 میرسیم (d کوچکترین مضرب مشترک مخرج دو عدد b,c است).حال فرض کنید (q,r,d) کوچکترین سه تایی مرتب طبیعی باشد که در این معادله صدق میکند.داریم:
میرسیم (d کوچکترین مضرب مشترک مخرج دو عدد b,c است).حال فرض کنید (q,r,d) کوچکترین سه تایی مرتب طبیعی باشد که در این معادله صدق میکند.داریم:
حالت دوم) حال اگر یکی از این اعداد مثلا a صفر باشد آنگاه به معادله
پس توانستیم به جوابی کوچکتر برسیم که تناقض است!
حالت سوم)در صورتی که دو تا از این اعداد مثلا b,c صفر باشند به معادله
 رسیده و به تناقض میرسیم!
رسیده و به تناقض میرسیم!
پس این معادله در اعداد گویا جواب ندارد.
حالت سوم)در صورتی که دو تا از این اعداد مثلا b,c صفر باشند به معادله
پس این معادله در اعداد گویا جواب ندارد.
آخرین ویرایش توسط مدیر
پاسخ : معادله ای در اعداد گویا .....
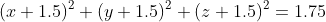
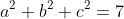
حال سه حالت را در نظر میگیریم:
حالت اول) اگر هر سه این اعداد ناصفر باشند،آنگاه کوچکترین مضرب مشترک مخرج این سه عدد را
 فرض میکنیم.حال مینویسیم:
فرض میکنیم.حال مینویسیم:

واقعا ممنونم :3:
با کمی ساده سازی داریم:
حال از سه تغییر متغیر
 استفاده کرده و معادله به معادله زیر تبدیل می شود:
استفاده کرده و معادله به معادله زیر تبدیل می شود:
حال سه حالت را در نظر میگیریم:
حالت اول) اگر هر سه این اعداد ناصفر باشند،آنگاه کوچکترین مضرب مشترک مخرج این سه عدد را
(
 ,
,
 )
)

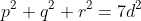

از آنجا که
 است و تنها حالت های ممکن برای یک عدد صحیح مربع کامل در مبنای 8،اعداد 0و1و4 هستند، در می یابیم که هیچ حالتی وجود ندارد.:3: پس این حالت نقض شد.
است و تنها حالت های ممکن برای یک عدد صحیح مربع کامل در مبنای 8،اعداد 0و1و4 هستند، در می یابیم که هیچ حالتی وجود ندارد.:3: پس این حالت نقض شد.
حالت دوم) حال اگر یکی از این اعداد مثلا a صفر باشد آنگاه به معادله
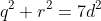 میرسیم (d کوچکترین مضرب مشترک مخرج دو عدد b,c است).حال فرض کنید (q,r,d) کوچکترین سه تایی مرتب طبیعی باشد که در این معادله صدق میکند.داریم:
میرسیم (d کوچکترین مضرب مشترک مخرج دو عدد b,c است).حال فرض کنید (q,r,d) کوچکترین سه تایی مرتب طبیعی باشد که در این معادله صدق میکند.داریم:
حالت دوم) حال اگر یکی از این اعداد مثلا a صفر باشد آنگاه به معادله
پس توانستیم به جوابی کوچکتر برسیم که تناقض است!
حالت سوم)در صورتی که دو تا از این اعداد مثلا b,c صفر باشند به معادله
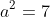 رسیده و به تناقض میرسیم!
رسیده و به تناقض میرسیم!
پس این معادله در اعداد گویا جواب ندارد.
حالت سوم)در صورتی که دو تا از این اعداد مثلا b,c صفر باشند به معادله
پس این معادله در اعداد گویا جواب ندارد.
پاسخ : معادله ای در اعداد گویا .....
از ۷ بودن سمت راست اگه استفاده نکنیم غلط میشه :23:، من متوجه نمیشم چجوری استفاده کردی از این. اگه میشه توضیح بده .
اون که جوابها کران دارند مساله رو تموم نمیکنه چون تو عددهای گویا هستیم :1:. مثلا معادله a^2 + b^2 =1 بی نهیات جواب داره تو عددهای گویا .
و نتیجه بگیرید بینهایت جواب وجود داردچون یه معادله درجه 1 برحسب xمیرسیم
اگر یک جواب داشته باشیم از طرفی میدانیم x,y,zهرسه تایی کرانه بالا دارند برای صدق کردن در رابطه.
اگر یک جواب داشته باشیم از طرفی میدانیم x,y,zهرسه تایی کرانه بالا دارند برای صدق کردن در رابطه.
اون که جوابها کران دارند مساله رو تموم نمیکنه چون تو عددهای گویا هستیم :1:. مثلا معادله a^2 + b^2 =1 بی نهیات جواب داره تو عددهای گویا .
