معادله ی دیفرانسیل معروف.
پاسخ : معادله ی دیفرانسیل معروف.
سلام آقا میلاد!!
این دو تا اثباتی که برای مشتق lnx گذاشتید به نظر من واقعا اثبات نیستند.معادله ی دیفرانسیل معروف. - صفحه 2
مثلا اثبات اولی.تعریف سود بانکی نپر.خودش موقع اثبات روش های مختلفی داره و تا اونجا که من می دونم توی همه روش هاش نیاز داره از lnx مشتق بگیریم!!
پس چه معنی ای داره از همین تعریف سود بانکی نپر بیاییم مشتق lnx رو تعریف کنیم؟
من این روش رو توی کتاب ریاضیات عمومی6 دیدم و واقعا شاخ در آوردم.به عنوان یه هم ارزی وسط راه حل کاملا بی دلیل استفاده کرده بود.
روش دوم هم توی کتاب توماس یا آدامز اینچور نوشته.دیگه واقعا از خنده داشتم روده بر میشدم.(فکر کنم آدامز)
همین جوری عشقی اومده بود گفته بود سطح زیر نمودار 1/x از 1 تا بینهایت میشه +lnx و از 1 تا 0 میشه lnx- . بعد حالا اومده بود مشتق لگاریتم x در مبنای a رو با مشقات فراوان و به سخخخختی از تعریف مشتق حساب کرده بود!!
مشکل من الان چیزاییه که نوشتم و هنوز هم قانع نشدم!
ریاضیات اینقدر هم نامنظم نیست که هرچیزی بی دلیل باشه !! :68:
برای اثبات مشتق lnX یه راهش استفاده از تعریف حدی e هستش :
روش بعدیش اینه که تابع lnX رو به صورت یه انتگرال تعریف میکنن و ثابت میکنند خواص لگاریتم رو داره و .... ! بعدش برای مشتقش هم از قضیه اساسی حساب استفاده میشه :
و بقیه روشها رو هنوز نمیدونم !!
برای اثبات مشتق lnX یه راهش استفاده از تعریف حدی e هستش :
روش بعدیش اینه که تابع lnX رو به صورت یه انتگرال تعریف میکنن و ثابت میکنند خواص لگاریتم رو داره و .... ! بعدش برای مشتقش هم از قضیه اساسی حساب استفاده میشه :
و بقیه روشها رو هنوز نمیدونم !!
سلام آقا میلاد!!
این دو تا اثباتی که برای مشتق lnx گذاشتید به نظر من واقعا اثبات نیستند.معادله ی دیفرانسیل معروف. - صفحه 2
مثلا اثبات اولی.تعریف سود بانکی نپر.خودش موقع اثبات روش های مختلفی داره و تا اونجا که من می دونم توی همه روش هاش نیاز داره از lnx مشتق بگیریم!!
پس چه معنی ای داره از همین تعریف سود بانکی نپر بیاییم مشتق lnx رو تعریف کنیم؟
من این روش رو توی کتاب ریاضیات عمومی6 دیدم و واقعا شاخ در آوردم.به عنوان یه هم ارزی وسط راه حل کاملا بی دلیل استفاده کرده بود.
روش دوم هم توی کتاب توماس یا آدامز اینچور نوشته.دیگه واقعا از خنده داشتم روده بر میشدم.(فکر کنم آدامز)
همین جوری عشقی اومده بود گفته بود سطح زیر نمودار 1/x از 1 تا بینهایت میشه +lnx و از 1 تا 0 میشه lnx- . بعد حالا اومده بود مشتق لگاریتم x در مبنای a رو با مشقات فراوان و به سخخخختی از تعریف مشتق حساب کرده بود!!
مشکل من الان چیزاییه که نوشتم و هنوز هم قانع نشدم!
- ارسال ها
- 1,326
- لایک ها
- 998
- امتیاز
- 113
پاسخ : معادله ی دیفرانسیل معروف.
جفتش درسته .من فراموش کردم بگم...روش اول که کاملن درسته.اولین بار برنولی اومد نپر تعریف کرد..بعدن نپر اومدلگاریتم اختراع کرد .یعنی ما هم همینکارو کردیم...با تعریف اصلی نپر اومدیم تابع معکوسش رو تعریف کردیم ln و مشتقش حساب کردیم.
روش دوم...یک روش دیگه است.که ملت میان با تعریف ln بشکل سطح زیر نمودار 1/x به این میرسن که تابع اکسپوتانسیل تابع معکوس ln .یعنی از این تعریف انتگرالیه شروع میکنند ومیرن تا ....الی ماشا الله!!
جفتش درسته .من فراموش کردم بگم...روش اول که کاملن درسته.اولین بار برنولی اومد نپر تعریف کرد..بعدن نپر اومدلگاریتم اختراع کرد .یعنی ما هم همینکارو کردیم...با تعریف اصلی نپر اومدیم تابع معکوسش رو تعریف کردیم ln و مشتقش حساب کردیم.
روش دوم...یک روش دیگه است.که ملت میان با تعریف ln بشکل سطح زیر نمودار 1/x به این میرسن که تابع اکسپوتانسیل تابع معکوس ln .یعنی از این تعریف انتگرالیه شروع میکنند ومیرن تا ....الی ماشا الله!!
پاسخ : معادله ی دیفرانسیل معروف.
4 تا تعریف از e اینجا هست که باید ثابت بشه هم ارز هستن ( یعنی یک e رو معرفی می کنن).
تعریف 1) e برابر پایه ی تابع نمایی است که مشتقش در صفر، برابر 1 باشد.
تعریف 2) e پایه ی لگاریتم طبیعی است که از انتگرال
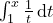تعریف می شود.
تعریف 3)
تعریف 4)
-------------------------------------------------------------------------------------------------------
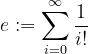
از تعریف (1) شروع می کنیم و بقیه ی تعاریف رو از اون نتیجه می گیریم، اثبات اینکه بقیه ی تعاریف هم تعریف (1) رو نتیجه میدن با برهان خلفه (که خیلی سادست):
اول نتایجی از (1) به دست می آوریم (فقط حق داریم از نمایی بودن و صفر بودن مشتق استفاده کنیم) :
پس
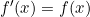. (نتیجه ی دیگر هم اینکه f پیوسته است)
تعریف (2) : f یک به یک است پس معکوس دارد، آن را با
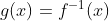نشان می دهیم. چون
پس
تابعی پیوسته است و
.
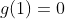طبق قاعده ی زنجیری (که اثباتش به e وابسته نیست) :
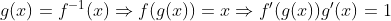اما از تعریف 1 داشتیم:
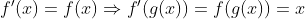از دو رابطه ی قبلی داریم:
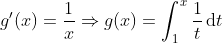پس معکوس تابع نمایی e^x (که لگاریتم با پایه ی e است) با لگاریتم طبیعی برابر است.
تعریف (3) : از تعاریف (1) و (2) و گرفتن لگاریتم از عبارت داخل حد و استفاده از قاعده ی هوپیتال به دست می آید.
تعریف (4) : فقط با استفاده از بسط تیلور و نتیجه ی تعریف (1) نتیجه ی مطلوب به دست می آید.
-------------------------------------------------------------------------------------------------------
برای مسئله ی اصلی هم فکر کنم بهتره دامنه رو مشخص کنید.
یک جواب بدیهی با دامنه ی R هم که کسی اشاره نکرد، تابع ثابت صفره!
4 تا تعریف از e اینجا هست که باید ثابت بشه هم ارز هستن ( یعنی یک e رو معرفی می کنن).
تعریف 1) e برابر پایه ی تابع نمایی است که مشتقش در صفر، برابر 1 باشد.
تعریف 2) e پایه ی لگاریتم طبیعی است که از انتگرال
تعریف 3)
تعریف 4)
-------------------------------------------------------------------------------------------------------
از تعریف (1) شروع می کنیم و بقیه ی تعاریف رو از اون نتیجه می گیریم، اثبات اینکه بقیه ی تعاریف هم تعریف (1) رو نتیجه میدن با برهان خلفه (که خیلی سادست):
اول نتایجی از (1) به دست می آوریم (فقط حق داریم از نمایی بودن و صفر بودن مشتق استفاده کنیم) :
تعریف (2) : f یک به یک است پس معکوس دارد، آن را با
طبق قاعده ی زنجیری (که اثباتش به e وابسته نیست) :
تعریف (3) : از تعاریف (1) و (2) و گرفتن لگاریتم از عبارت داخل حد و استفاده از قاعده ی هوپیتال به دست می آید.
تعریف (4) : فقط با استفاده از بسط تیلور و نتیجه ی تعریف (1) نتیجه ی مطلوب به دست می آید.
-------------------------------------------------------------------------------------------------------
برای مسئله ی اصلی هم فکر کنم بهتره دامنه رو مشخص کنید.
یک جواب بدیهی با دامنه ی R هم که کسی اشاره نکرد، تابع ثابت صفره!