نظریه اعداد 2
پاسخ : نظریه اعداد 2
به وضوح شرط لازمی که هست اینه که
 . نشون میدیم این شرط کافی هم هست. برای
. نشون میدیم این شرط کافی هم هست. برای
 هایی که نسبت به
هایی که نسبت به
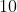 اول هستند حکم بدیهیست، چون برای اون ها
اول هستند حکم بدیهیست، چون برای اون ها
}&space;-&space;1) . برای اعداد توان
. برای اعداد توان
 احکام زیر که قوی تر هم هستند را می توان ثابت کرد :
احکام زیر که قوی تر هم هستند را می توان ثابت کرد :
حکم 1 : برای هر عدد طبیعی
 ، دقیقا یک عدد
، دقیقا یک عدد
 رقمی با ارقام
رقمی با ارقام
 موجود است که بر
موجود است که بر
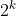 بخش پذیر باشد.
بخش پذیر باشد.
حکم 2 : برای هر عدد طبیعی
 ، دقیقا یک عدد
، دقیقا یک عدد
 رقمی با ارقام
رقمی با ارقام
 موجود است که بر
موجود است که بر
 بخش پذیر باشد.
بخش پذیر باشد.
به وضوح شرط لازمی که هست اینه که
حکم 1 : برای هر عدد طبیعی
حکم 2 : برای هر عدد طبیعی
آخرین ویرایش توسط مدیر
پاسخ : نظریه اعداد 2
من هم تا همین قسمت حل رفته بودم اما قسمتی از حل سوال می ماند .این که عدد ما به صورت مضربی از توان 2 باشد که عامل فرد نیز داشته باشد و به همین صورت برای توان 5 (دارای عاملی باشد که نسبت به 5 اول است ) .
به وضوح شرط لازمی که هست اینه که
 . نشون میدیم این شرط کافی هم هست. برای
. نشون میدیم این شرط کافی هم هست. برای
 هایی که نسبت به
هایی که نسبت به
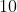 اول هستند حکم بدیهیست، چون برای اون ها
اول هستند حکم بدیهیست، چون برای اون ها
}&space;-&space;1) . برای اعداد توان
. برای اعداد توان
 احکام زیر که قوی تر هم هستند را می توان ثابت کرد :حکم 1 : برای هر عدد طبیعی
احکام زیر که قوی تر هم هستند را می توان ثابت کرد :حکم 1 : برای هر عدد طبیعی
 ، دقیقا یک عدد
، دقیقا یک عدد
 رقمی با ارقام
رقمی با ارقام
 موجود است که بر
موجود است که بر
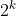 بخش پذیر باشد.حکم 2 : برای هر عدد طبیعی
بخش پذیر باشد.حکم 2 : برای هر عدد طبیعی
 ، دقیقا یک عدد
، دقیقا یک عدد
 رقمی با ارقام
رقمی با ارقام
 موجود است که بر
موجود است که بر
 بخش پذیر باشد.
بخش پذیر باشد.
پاسخ : نظریه اعداد 2
اصلش ساختن اون اعداد
 رقمی هست. مثلا برای ساخت مضربی برای عددی مثل
رقمی هست. مثلا برای ساخت مضربی برای عددی مثل
 که
که
=1) اینطور عمل می کنیم، فرض کنید
اینطور عمل می کنیم، فرض کنید
 عددی
عددی
 رقمی با ارقام ناصفر است که بر
رقمی با ارقام ناصفر است که بر
 بخشپذیر است. در این صورت با
بخشپذیر است. در این صورت با
) بار پشت سر هم نوشتن
بار پشت سر هم نوشتن
 ، عددی برابر
، عددی برابر
k}.m&space;=&space;m&space;.&space;\frac{10^{am}&space;-&space;1}{10^m&space;-&space;1}) خواهیم داشت که طبق لم دو خط بر
خواهیم داشت که طبق لم دو خط بر
 و در نتیجه بر
و در نتیجه بر
 بخشپذیر است و چون
بخشپذیر است و چون
 با ارقام ناصفر است، در شرایط مسئله کار می کند.
با ارقام ناصفر است، در شرایط مسئله کار می کند.
اصلش ساختن اون اعداد
