هندسه صفر تا 100
پاسخ : هندسه صفر تا 100
میشه ادامه راه جبریشو بذاری یا یه توضیح مختصری بدی؟
ممنون.
لم:
^{2})
حالا اگه DEF هم خط باشد مساحت مثلث DEF صفر میشه و حکم ثابت میشه.
اثبات لم:
از سوال 5 صفحه 259 هندسه احمدپور داریم که مثلثی که از پا تصاویر N(مرکز دایره نه نقطه) بوجود میاد با مثلث DEF به نسبت 1/4 متجانس هستش.
ادامش فقط کار جبری لازمه.
حالا اگه DEF هم خط باشد مساحت مثلث DEF صفر میشه و حکم ثابت میشه.
اثبات لم:
از سوال 5 صفحه 259 هندسه احمدپور داریم که مثلثی که از پا تصاویر N(مرکز دایره نه نقطه) بوجود میاد با مثلث DEF به نسبت 1/4 متجانس هستش.
ادامش فقط کار جبری لازمه.
ممنون.
پاسخ : هندسه صفر تا 100
خب اگر این تجانس ثابت بشه، چون N روی دایره محیطی قرار داره پس مثلث پایی اش یک خط هستش. پس مساله با قضیه ی خط سیمسون حل میشه. ضمن این که اگر اشتباه نکنم اون لمی که نوشتید حالت خاص قضیه برای محاسبه ی مساحت مثلث پایی قضیه ی اویلر هستش. سعی کنید با درونیابی اثباتش کنید.
خوبه این مساله رو با مختلط هم حل کنید. دکتر افتخاری یک جزوه ای در مورد مختلط نوشتن که خوبه بخونیدش. یا می تونید کتاب Untitled Page رو بخونید.
حالا سوال جدید:
خط
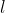 اضلاع مثلث
اضلاع مثلث
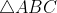 را در نقاط
را در نقاط
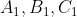 قطع می کند. نقطه ی
قطع می کند. نقطه ی
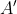 وسط پای عمود
وسط پای عمود
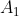 بر اضلاع
بر اضلاع
 است.
است.
الف) ثابت کنید
 روی یک خط مانند
روی یک خط مانند
 قرار دارند.
قرار دارند.
ب) ثابت کنید اگر
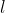 از مرکز دایره ی محیطی
از مرکز دایره ی محیطی
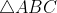 بگذرد آنگاه
بگذرد آنگاه
 از مرکز دایره ی نه نقطه ی
از مرکز دایره ی نه نقطه ی
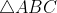 می گذرد.
می گذرد.
------------
منبع سوال:
المپیاد هندسه ی شاریگین 2011.
------------
*سعی کنید قسمت ب رو با مختلط و بدون هم حل کنید.
------------
سایت المپیاد هندسه ی شاریگین: IX Olimpiada imeni I.F.Sharygina
یک منبع غنی از سوالات هندسه هستش. سوالتش در سطح خوبی قرار دارن.
------------
این هم یک سایت برای سوالات المپیاد روسی: Задачи
من خودم سوالای شاریگین رو حل کردم ولی سوالای این سایت بالایی رو نه. ولی خب مباحثش با سر فصل های مباحث المپیاد میخونه و از سایت شاریگین بهش رسیدم.:3:
سایت شاریگین روسی ه ولی سوالاش ترجمه ی انگلیسی داره. سایت بالایی کاملا روسی نوشته شده ولی خب می تونید به گوگل بگید براتون ترجمه کنه.
----------
لم:
^{2})
حالا اگه DEF هم خط باشد مساحت مثلث DEF صفر میشه و حکم ثابت میشه.
اثبات لم:
از سوال 5 صفحه 259 هندسه احمدپور داریم که مثلثی که از پا تصاویر N(مرکز دایره نه نقطه) بوجود میاد با مثلث DEF به نسبت 1/4 متجانس هستش.
ادامش فقط کار جبری لازمه.
حالا اگه DEF هم خط باشد مساحت مثلث DEF صفر میشه و حکم ثابت میشه.
اثبات لم:
از سوال 5 صفحه 259 هندسه احمدپور داریم که مثلثی که از پا تصاویر N(مرکز دایره نه نقطه) بوجود میاد با مثلث DEF به نسبت 1/4 متجانس هستش.
ادامش فقط کار جبری لازمه.
خوبه این مساله رو با مختلط هم حل کنید. دکتر افتخاری یک جزوه ای در مورد مختلط نوشتن که خوبه بخونیدش. یا می تونید کتاب Untitled Page رو بخونید.
حالا سوال جدید:
خط
الف) ثابت کنید
ب) ثابت کنید اگر
------------
منبع سوال:
المپیاد هندسه ی شاریگین 2011.
------------
*سعی کنید قسمت ب رو با مختلط و بدون هم حل کنید.
------------
سایت المپیاد هندسه ی شاریگین: IX Olimpiada imeni I.F.Sharygina
یک منبع غنی از سوالات هندسه هستش. سوالتش در سطح خوبی قرار دارن.
------------
این هم یک سایت برای سوالات المپیاد روسی: Задачи
من خودم سوالای شاریگین رو حل کردم ولی سوالای این سایت بالایی رو نه. ولی خب مباحثش با سر فصل های مباحث المپیاد میخونه و از سایت شاریگین بهش رسیدم.:3:
سایت شاریگین روسی ه ولی سوالاش ترجمه ی انگلیسی داره. سایت بالایی کاملا روسی نوشته شده ولی خب می تونید به گوگل بگید براتون ترجمه کنه.
----------
پاسخ : هندسه صفر تا 100
من اثبات قضیه اویلرو به صورت هندسی دیدم(با قوت هستش اینم لینک حل)
من تا حالا حل مسئله هندسه با درون یابی لاگرانژ ندیدم میتونین حلشو بذارین(اگه وقت داشتین)
خب اگر این تجانس ثابت بشه، چون N روی دایره محیطی قرار داره پس مثلث پایی اش یک خط هستش. پس مساله با قضیه ی خط سیمسون حل میشه. ضمن این که اگر اشتباه نکنم اون لمی که نوشتید حالت خاص قضیه برای محاسبه ی مساحت مثلث پایی قضیه ی اویلر هستش. سعی کنید با درونیابی اثباتش کنید.
-
-
من تا حالا حل مسئله هندسه با درون یابی لاگرانژ ندیدم میتونین حلشو بذارین(اگه وقت داشتین)
پاسخ : هندسه صفر تا 100
برای اینکه این ماراتن راه بیفته سوال بعدی رو میزارم البته یه سوال Aref هنوز جواب داده نشده.
دایره های z,y یکدیگر رو در O , M قطع میکنند.دایره x به مرکز O دایره های z,y را در چهار نقطه A,B,C,D قطع میکنند به طوری چهارضاعی ABCD محدب هستش.خطوط AB و CD همدیگرو در E و خطوط AD و BC یگذیگرو در F قطع میکنند و AC,BD یکدیگرو در K قطع میکنند.ثابت کنید یا MO بر EF عمود است یا بر EK .
برای اینکه این ماراتن راه بیفته سوال بعدی رو میزارم البته یه سوال Aref هنوز جواب داده نشده.
دایره های z,y یکدیگر رو در O , M قطع میکنند.دایره x به مرکز O دایره های z,y را در چهار نقطه A,B,C,D قطع میکنند به طوری چهارضاعی ABCD محدب هستش.خطوط AB و CD همدیگرو در E و خطوط AD و BC یگذیگرو در F قطع میکنند و AC,BD یکدیگرو در K قطع میکنند.ثابت کنید یا MO بر EF عمود است یا بر EK .
پاسخ : هندسه صفر تا 100
می شه فرض کنید زاویه edc بزرگ تر از ecd است و یکبار هم فرض کنید کوچکتر ! بعد به تناقض می خوردید و ... !
اینم جواب سوال 5 :

پس برای اثبات حکم کافیست بگوییم که زاویه ی ceq 60 درجه است
)
)
,&space;eh=\frac{ae}{2}\left&space;(&space;\sqrt{2-\sqrt{3}}&space;\right&space;))
}{\frac{ae}{2}\left&space;(&space;\sqrt{2+\sqrt{3}}&space;\right&space;)}&space;=2\left&space;(&space;1-\frac{1}{2}\sqrt{\frac{2-\sqrt{3}}{2+\sqrt{3}}}&space;\right&space;)=&space;2\left&space;(&space;1-1+\frac{\sqrt{3}}{2}&space;\right&space;)=\sqrt{3}\rightarrow&space;\tan&space;ceq=\sqrt{3}\rightarrow&space;\angle&space;ceq=60)
اینم شکل سوال :

اگر کسی راه بهتر و کوتاه تری داره منم خوشحال میشم بزاره
خب دیگه از این به بعد میریم سر سوالای ست تر (البته این سوال به نظر من که سخت بود به نظر شما چی ؟)
پس برای اثبات حکم کافیست بگوییم که زاویه ی ceq 60 درجه است
اینم شکل سوال :

اگر کسی راه بهتر و کوتاه تری داره منم خوشحال میشم بزاره
خب دیگه از این به بعد میریم سر سوالای ست تر (البته این سوال به نظر من که سخت بود به نظر شما چی ؟)
پاسخ : هندسه صفر تا 100
سلام!از اونجایی که کنکور تموم شده و دوره تابستون هم شروع شده(!) یه سوال میذارم،باشد که این تاپیک دوباره بیاد بالا:
AoPS Forum - RMM 2013 Problem 3 • Art of Problem Solving
سوال بامزه ایه...
اگه کسی ترجمه خواست بگه...
سلام!از اونجایی که کنکور تموم شده و دوره تابستون هم شروع شده(!) یه سوال میذارم،باشد که این تاپیک دوباره بیاد بالا:
AoPS Forum - RMM 2013 Problem 3 • Art of Problem Solving
سوال بامزه ایه...
اگه کسی ترجمه خواست بگه...
پاسخ : هندسه صفر تا 100
بابا تورو خدا یکی سر به این تایپیک بزنه پاسخ پرسش ما رو بده.http://www.irysc.com/forum/t12297/#post172842
بابا تورو خدا یکی سر به این تایپیک بزنه پاسخ پرسش ما رو بده.http://www.irysc.com/forum/t12297/#post172842
پاسخ : هندسه صفر تا 100
ممنون میشم اگه فارسیشو بزنین
سلام!از اونجایی که کنکور تموم شده و دوره تابستون هم شروع شده(!) یه سوال میذارم،باشد که این تاپیک دوباره بیاد بالا:
AoPS Forum - RMM 2013 Problem 3 • Art of Problem Solving
سوال بامزه ایه...
اگه کسی ترجمه خواست بگه...
AoPS Forum - RMM 2013 Problem 3 • Art of Problem Solving
سوال بامزه ایه...
اگه کسی ترجمه خواست بگه...
