ویژه بردارها و ویزه مقدار های یک ماتریس

[seyed iman]

برای یک ماتریس nxn ویزه مقادیر رو داریم(n تا مستقل)
حالا ویزه بردار چجوری بدست بیاریم؟هر کدوم ممکنه چند تا درآد!!
توان n ماتریسمون چی میشه؟؟

 

[goodarz]

پاسخ : ویژه بردارها و ویزه مقدار های یک ماتریس

خوب اون بردار ویژه باید عضو فضای پوچ A-aI باشه که a اون مقدار ویژه هست....چون فضا پوچ یه ماتریس یه زیرفضا از فضای کلیه پس اگه فقط 0 نباشه بعدش حداقل یکه.....

 

[seyed iman]

پاسخ : ویژه بردارها و ویزه مقدار های یک ماتریس

عزیزم.قشنگم.جواب بده!!
ویژه ماتریس ها لاندا آی و ویژه بردار متناظر آلفا آی.
آلفا آیم بدست باید بیاری.
بعد جواب.من فکر میکنم میشه زیگما لاندا آی آلفا آی روی آی ولی شک دارم.

 

[goodarz]

پاسخ : ویژه بردارها و ویزه مقدار های یک ماتریس

فکر نمی کنم هیچ روش کلی واسه به دست آوردن بردار ویژه های یه ماتریس وجود داشته باشه.....مقدار ویژه هارو میشه با چندجمله ای مشخصه ماتریس در آورد, ولی تو کتابایی که من دیدم همشون بردار ویژه رو دستی و با توجه به خود اون مقدار ویژه به دست آوردن.

 

[seyed iman]

پاسخ : ویژه بردارها و ویزه مقدار های یک ماتریس

خب میگم داریم ویژه مقدارارو.
درست بخون....ویزه مقدارو داریم>ویژه بردار؟؟؟؟>توان n ماتریس؟

 

[goodarz]

پاسخ : ویژه بردارها و ویزه مقدار های یک ماتریس

آقا جان منم گفتم که, بردار ویژه رو با در دست داشتن مقدار ویژه اون به طور دستی میشه پیدا کرد, راه کلی نداره, اگه باور نداری بگرد ببین تو این چیزی پیدا می کنی یا نه:

Hand book of linear algebra-Leslie Hogben

یه دایرۀالمعارف کامل واسه جبر خطی....

 

[amir.ekhlasi]

پاسخ : ویژه بردارها و ویزه مقدار های یک ماتریس

ببینید. اگر یک ماتریس دلخواه را به ما داده باشند، ما میتونیم مقدار ویژه های آن را به دست بیاوریم. (پیدا کردن ریشه های چند جمله ای مشخصه) پس اگر با دانستن مقدار ویژه ها بتونیم بردار ویژه ها را به دست بیاریم، یعنی در کل اگر یک ماتریس را به ما بدن ما میتونیم بردار ویژه ها را به دست بیاریم که راه حلی با درجه چند جمله ای وجود نداره. (زیرا پیدا کردن بردار ویژه ها معادل با پیدا کردن هسته یک تبدیل خطیه) پس حرف گودرز درسته. حتی در این حد بگم که وجود بردار و مقدار ویژه برای یک ماتریس در فضای حقیقی (فضای اقلیدسی) را با ابزارهای مثل حساب دیفرانسیل و انتگرال (قضیه استوکس) یا توپولوژی جبری (قضیه تقطه ثابت براوئر) ثابت میکنند. یعنی خیلی بستگی به میدانمون داره.

 

[seyed iman]

پاسخ : ویژه بردارها و ویزه مقدار های یک ماتریس

مرسی از اخلاصی و گودرز.ببین من میخوام ببینم چیزی که برا توان ان ام حدس میزنم درسته یا نه و دوم
اینکه ویژه بردار یک ماتریس nxn چند در چنده و چجوری حساب میشه.
آخه من با اون چیزی که میدونستم به مشکل خوردم.

 

[amir.ekhlasi]

پاسخ : ویژه بردارها و ویزه مقدار های یک ماتریس

ویژه بردار، یک بردار. درواقع مجموعه ویژه بردارها یک زیرفضای برداری از فضای برداری اصلیمونه. منظور از چند در چنده را نمیفهمم. بعد هم حدستون در مورد توان n ام چیه؟ اصلا در مورد چیه؟ درواقع ویژه بردار ماتریس A بردار X (ماتریس عمودی یک در n) است که به ازای اسکالری مانند b (مقدار ویژه) داشته باشیم AX=bX.

 

[seyed iman]

پاسخ : ویژه بردارها و ویزه مقدار های یک ماتریس

من فکر میکنم [توان n ماتریسمون]میشه زیگما لاندا آی آلفا آی روی آی ولی شک دارم.

میدونم تعریف ویژه بردارو.مثلن یک ماتریس nxn با درایه های معلوم و ویژه مقدار های معلوم داریم.ویژه بردار متناظر با ویژه مقدار مثلن لاندای آی را بنویسید.
این ویژه برداره مگه خودش یک ماتریس نیست.یعنی مگه بشکل یه ماتریس نمینویسیمش؟

 

[goodarz]

پاسخ : ویژه بردارها و ویزه مقدار های یک ماتریس

بله, این ویژه بردار خودش یه ماتریس ستونیه, و در واقع مجموعه ویژه بردارا واسه یه ویژه مقدار خودشون تشکیل یه زیر فضا میدن, ولی هیچ الگوریتم معینی واسه پیدا کردنش وجود نداره.

 

[seyed iman]

پاسخ : ویژه بردارها و ویزه مقدار های یک ماتریس

خب این به کنار.من یه جا دیدم توان N یک ماتریس رو با رابطه زیگمای لاندا آی بتوان n ضربدر آلفا آی حساب کرد.
چجوری؟چرا؟
اینو تو یه فیلم کلاش MIT دیدم.
Eigenvalues and Eigenvectors Help Video in College Math Linear Algebra -- Free Math Help Videos Online by MathVids.com

 

[goodarz]

پاسخ : ویژه بردارها و ویزه مقدار های یک ماتریس

آقا فیلمش خیلی زیاده!! اگه زحمتی نیست یه خلاصشو بگو. ممنون

 

[seyed iman]

پاسخ : ویژه بردارها و ویزه مقدار های یک ماتریس

آقا همون معدله ای که گفتی و بعد گفتی میره تو NullSPace و از این صحبت ها.
بعد هم یه بحث دیگه میکنه میاد ماتریس قطری میکنه.و با ضرب ماتریسمون در قطری شدش هی میاد ساده میکنه و به اونمیرسه.فیلمش خیلی قشنگه ها!!توصیه میکنم ببینید.
خلاصه میگه ماتریس رو میشه با ویژه مقادیر و ویژه بردارش به نوعی تجزیه کرد.و همینطوری اومده گفته اون رابطهای که من میگم.
یه بخشیش تو اون لینکه یه بخشی هم تو همون سایت و به اسمDiagonalization هست.

 

[amir.ekhlasi]

پاسخ : ویژه بردارها و ویزه مقدار های یک ماتریس

اون فیلمی که من دیدم همون چیزی را گفت که من گفتم. اون اول ویژه مقدارها را با پیدا کردن ریشه های چند جمله ای مشخصه پیدا کردن و با چند معادله چند مجهول بردار ویژه ها را پیدا کرد. اون لینک دومت رو بده.

 

[goodarz]

پاسخ : ویژه بردارها و ویزه مقدار های یک ماتریس

من که فیلمرو ندیدم (دانلودش نصف روز طول می کشه!!!!) ولی اون طوری که از حرفاتون فهمیدم, واسه پیدا کردن اون بردار ویژه ها, واسه اینکه بتونه اون دستگاه n معادله n مجهول رو حل بکنه, میاد از روش قطری سازی (Diagonalization ) استفاده می کنه. همون طوری که تو این لینکه گفته: Diagonalizable matrix - Wikipedia, the free encyclopedia :

Diagonalizable matrices and maps are of interest because diagonal matrices are especially easy to handle: their eigenvalues and eigenvectors are known and one can raise a diagonal matrix to a power by simply raising the diagonal entries to that same power

یعنی واسه یه ماتریس قطری یا ماتریسی که بشه به یه ماتریس قطری تبدیلش کرد مقدار ویژه ها و بردار ویژه ها رو میشه راحت به دست آورد, ولی نکته اینجاست که همه ماتریسارو نمیشه قطری کرد:

Defective matrix - Wikipedia, the free encyclopedia

.....

 

[seyed iman]

پاسخ : ویژه بردارها و ویزه مقدار های یک ماتریس

Diagonalizing a matrix and Powers of A Help Video in College Math Linear Algebra -- Free Math Help Videos Online by MathVids.com
مرسی که قبلی رو دیدی.

 

[seyed iman]

پاسخ : ویژه بردارها و ویزه مقدار های یک ماتریس

به گودرز :آره همینو میگم.
از نظر فیزیکی سیستم های defective برای ما آشنان و میدونیم که نباید قطری بشن.و مساله EPR که بزرگترین پارادوکس علمه و انیشتن و همکاراش اونو بعنوان یه مشکل برای کوانتوم میدیدن به این مربوطه.
ولی سوالم اینه که اگر ماتریسی قطری میشد چجوری توان n رو بدست آوریم.رابطش؟

 

[goodarz]

پاسخ : ویژه بردارها و ویزه مقدار های یک ماتریس

خوب ببین اگه یه ماتریس قطری بشه یعنی چی؟ یعنی یه ماتریس وارون پذیر مثل

هست که

که

خودش یه ماتریس قطری باشه, قبول؟
حالا واسه توان

امش, استقرایی بساز:

فرض استقرا:

حکم:

.

حالا واسه اینکه از فرض به حکم برسیم,

که این حکمو ثابت می کنه.

حالا به دوتا نکته باید توجه کرد, اولیش اینکه

قطریه, و ثانیا اینکه اگه

یه مقدار ویژه واسه

باشه, اونوقت

یه مقدار ویژه واسه

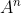هست و برعکس. یعنی اگه بشه یه ماتریس رو قطری کرد, تواناشم میشه, و حالا که قطری شده و مقدار ویژه هاشو میدونیم بردار ویژه هاشم میشه راحت به دست آورد. غلطه حرفم؟؟؟

 

[seyed iman]

پاسخ : ویژه بردارها و ویزه مقدار های یک ماتریس

نه دیگه این مث اون رابطه ایه که گفتم فقط مشکلش اینه توان n ماتریس ما یک ماتریس nxn است ولی ویزه بردارهامون چی؟یعنی باید ویژه بردار ها nxn باشن تا بشه از جمع کردنشون به A رسید.