.:: چند نکته در باره ی جبر در المپیاد ریاضی ::.

math · 1393/3/14

سلام

تقریبا یک سال پیش یک سری تاپیک هایی برای یاد گیری چند جمله ای و تابعی زده شده بود و تقریبا نتیجه گیری نهایی همه ی اونها خوندن کتاب اقای صفا بوده . من تصمیم گرفتم در پست های مختلف نکته هایی که در این کتاب نیست ( یا اگر هستش خیلی پررنگ نیستش . ) رو بذارم . یک سری روش هایی در نامساوی و چند جمله ای به خصوص هستش که ممکنه مساله رو براتون حل نکنه ولی دید و شهود خوبی بهتون میده برای حل مسائل . در پست اول من هر 3 مبحث رو شروع میکنم و یه سری نکاتی رو مینویسم با همون ویژگی های بالا :4: . ( باز هم میگم در نکات زیر این موضوع در نظر گرفته شده که شما کتاب اقای صفا رو مطالعه کردید و شناختی از چند جمله ای و اعداد مختلط و تعریف تابع و یه سری نامساوی مثل کوشی و حسابی هندسی دارید . این نکات لزوما در سطح مرحله دو نیستن ! ولی بهتون دید خوبی در حل مساله میدن . این مباحث به ترتیب نیستن یعنی ممکنه پست دوم مباحث ساده تری نسبت به پست اول داشته باشه . البته پست دوم زمانی میاد که استقبال خوبی از پست اول شده باشه :4

مساله هایی که برای آشنایی آورده شده مساله های بسیار سختی هستند و حل کردن آنها لزومی ندارد . ولی فکر کردن به آنها باعث آشنایی بیشتر میشود .

چند جمله ای :

1-معادلات چند جمله ای :

الف) ریشه چند جمله ای ها :

در معادلات چند جمله ای خیلی خوبه که شما یه شهودی نسبت به ریشه های چند جمله ای داشته باشید . ( توجه کنید که شما با دونستن حتی یک ریشه چند جمله ای میتونید معادله چند جمله ای رو راحت تر بنویسید . )

در زمان کار کردن با ریشه ها شما بهتره که با اعداد حقیقی کار کنید ولی ریشه ها ممکنه که مختلط باشن !!! برای همین بهترین ایده برای صحبت کردن در باره ریشه ها صحبت کردن و شناخت رو قدر مطلق ریشه ها ( یا همون نرم ریشه هاست ) . یک مثال برای معادلات چند جمله که براشون باید با نرم ریشه ها کار کنیم : http://www.irysc.com/forum/t17135/

یکسری از معادلات چند جمله ای به راحتی بالا نیستن !! یعنی شما بیشترین شناختی که میتوانید روی ریشه ها پیدا کنید مساله را حل نمیکنند !!! یعنی مثلا شما با بررسی اطلاعات مساله به این موضوع میرسید که نرم تمام ریشه ها 1 است . ولی تمام اعداد روی دایره واحد ویژگی فوق را دارند ! برای درک بهتر این مطلب ابتدا روی سوال زیر فکر کنید :

تمام چند جمله ای ها با ضرایب حقیقی را بیابید که :

$P(x)P(2x^{2})=P(2x^{3}+x)$

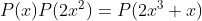
( راهنمایی : ثابت کنید نرم ریشه ها برابر 1 است . حال توجه کنید به معادله ی اصلی و توجه به ادامه ی مطلب .)
اعداد مختلط ویژگی کامل تری نسبت به نرم نیز دارند که فوق العاده کاربرد داره ! این ویژگی نمایش قطبی آنهاست . ( در کتاب اقای صفا توضیح داده شده است .)

در نمایش قطبی اعداد علاوه بر توجه به نرم عدد مختلط به ارگومان ان نیز توجه میشود !!

برای اشنایی بیشتر با ارگومان سعی کنید روی این مساله فکر کنید : فرض کنید سه عدد

$\alpha ,\beta ,\theta \in \left [ 0,2\Pi \right ]$

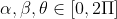به طوری که :

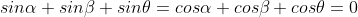
$sin\alpha +sin\beta +sin\theta =cos\alpha +cos\beta +cos\theta=0$

ثابت کنید که :

$cos2\alpha +cos2\beta +cos2\theta=0$

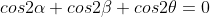
( راهنمایی : این سه زاویه ارگومان های راس های یک مثلث متساوی الاضلاع هستند .)

حال که توسط این مساله اشنایی بیشتری با ارگومان پیدا کردید سعی کنید ادامه ی معادله ی چند جمله ای بالا را با در نظر گرفتن ارگومان ریشه ها حل کنید .

زمانی که ما ارگومان و نرم یه عدد را بشناسیم میتونیم اون عدد رو بدست بیاریم و وقتی ریشه های یه چند جمله ای رو بشناسیم میتونیم اون چند جمله ای رو بدست بیاریم .

برای این ایده چند مساله میاوریم که به ترتیب سختی مرتب شده اند و برعکس سوالات بالا انتظار میرود که حل شوند :

1-تمام چند جمله ای ها با ضرایب حقیقی رو بیابید که :

$P(x^{2})P(x^{3})=P(x)^{5}$

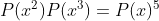
(راه حل :AoPS Forum - polynomial equation • Art of Problem Solving )

2-تمام چند جمله ای ها با ضرایب حقیقی رو بیابید که :

$P(x^{2}-1)=P(x)P(-x)$

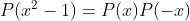
(راه حل :AoPS Forum - P(x^2-1)=p(x)p(-x) • Art of Problem Solving )

3-تمام چند جمله ای ها با ضرایب حقیقی رو بیابید که :

$P(x^{2})=P(x)P(x-1)$

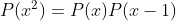
(راه حل :AoPS Forum - Find all real polynomials • Art of Problem Solving )

4-تمام چند جمله ای ها با ضرایب حقیقی رو بیابید که :

$P(2x^{2})P(x)=P(2x^{3}+x^{2})$

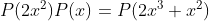
(راه حل : AoPS Forum - Polynomial • Art of Problem Solving )

5- تمام چند جمله ای ها با ضرایب حقیقی رو بیابید که :

$P(x^{2})=P(x)^{2}$

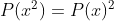
(راه حل : بسیار ساده است .:4

6- تمام چند جمله ای ها با ضرایب حقیقی رو بیابید که :

$P(x^{n})=P(x)^{n}$

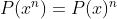(راه حل : بسیار ساده است .:4

نامساوی :

(اخطار : در این پست برای نامساوی ها یک روش فوق العاده قوی برای حل مساله رو معرفی میکنیم ! این روش در صورت عدم تسلط باعث میشه که خیلی از نامساوی هایی را که به راحتی حل میشوند رو به سختی حل کنید یا حتی حل نکنید !! خیلی از با تجربه های المپیاد خوندن این روش ها رو توصیه نمیکنن ولی من این جا اوردم:4:)

1 - روش

$uvw$

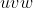: قبل از بیان این روش و ایده های نداشته آن :4: ابتدا یه قضیه رو بیان میکنیم که این قضیه کمکی به حل مساله نمیکند بلکه یه اطمینان است که یکسری نامساوی ها با این روش حل میشوند و یه سری مسائل قطعا حل نمیشود !!!!

به طور خلاصه این قضیه بیان میکند که اگر یک چند جمله ای n متغیره داشته باشیم و این چند جمله ای متقارن باشد انگاه میتوان ان را توسط متقارن های ابتدایی نوشت ! برای خوندن کامل این قضیه به این جا مراجعه کنید : Newton's identities - Wikipedia, the free encyclopedia به این قضیه قضیه نیوتن میگویند .

حال روش و قضیه های

$uvw$

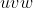رو بیان میکنیم و ارتباطش را با قضیه ی نیوتن بیان میکنیم . فرض کنید سه عدد حقیقی مثبت داده شده داریم . انگاه

$u,v^{2},w^{3}\in \mathbb{R}^{+}$

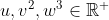وجود دارند که :

$a+b+c=3u$

$ab+cb+ac=3v^{2}$

$abc=w ^{3}$

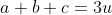
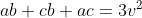
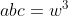
قضیه 1 : داریم :

$u\geq v\geq w$

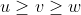. اثبات این قضیه توسط نامساوی حسابی -هندسه بسیار راحت است .

از بیان قضیه های فرعی

$uvw$

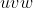خودداری میکنم و به بررسی قضیه اصلی ان میپردازیم :

قضیه

$uvw$
:

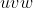اگر هر دو تا از

$u, v, w$

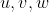را ثابت نگهداریم آنگاه سومی مینیمم دارد اگر دو تا از

$a, b, c$

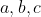برابر باشند یا یکی 0 باشد ! و ماکسیمم دارد اگر دو از

$a, b, c$

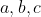باهم برابر باشند .

پس اگر بتوانیم یک نامساوی را برحسب

$u, v, w$

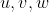بنویسیم و اجازه ثابت نگهداشتن دو تا از انها را داشته باشیم کافی است نامساوی را برای دو تا برابر یا یکی صفر حل کنیم !!

حال توجه کنید که با توجه به قضیه نیوتن اگر یک نامساوی متقارن نباشد نمیتوان از

$uvw$
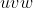استفاده کرد !! چون قطعا نمیتوان به صورت خواسته شده نوشتش !

حال برای اشنایی بیشتر خوب است که یکم روی سوال 3 امسال مرحله 2 با

$uvw$
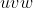فکر کنید !

زمانی که از روش

$uvw$
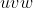استفاده میکنیم دیگه ایده ای در کار نیست و باید بتوانیم به خوبی نامساوی را محاسبه کنیم !

یک ایده خوبی برای نامساوی های متقارن و همگن وجود داره اینه که شما میتونید زمانی که از uvw استفاده کردید و دو تا از متغییر ها با هم برابر شدند میتوانید چون که نامساوی همگن است تمام متغیر ها را بر ( مینیمم یا ماکسیمم یا اون دو عبارتی که با هم برابر شدند ) تقسیم کنیم ( چرا ؟:4

با این کار محاسباتمان به سادگی انجام میگیرد !

البته کلا اگر در یک مساله نامساوی دیدید که به نتیجه ای نرسیدید و تصمیم گرفتید محاسبه کنید این ایده بسیار خوب است که اگر نامساوی همگن بود ان ها را بر مینیمم یا ماکسیمم
تقسیم کنید . پس یکی از متغیر ها یک میشود و محاسباتتان راحت تر میشود .

به دلیل اینکه این یک روشی است که بسیار قوی است چون تقریبا بیشتر نامساوی هایی که ما میبینیم متقارن و یا همگن هستند ، بهتر است این روش را همیشه به عنوان یک روش کمکی در ذهن داشته باشید و سعی کنید زیاد از این روش استفاده نکنید :4:

برای قوی تر شدن در این روش بهترین کار حل مسئله است برای همین در زیر یک سری مساله اورده شده که با

$uvw$
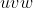حل میشوند.

تمام مسائل زیر برای اعداد نا منفی هستند و باید انها را ثابت کنید :

1-

$\left\Big(\sum_{cyc}xy\right\Big)\cdot\left\Big(\sum_{cyc}\frac{1}{(x+y)^2}\right\Big)\geq\frac{9}{4\cdot\left\Big[ 1-\prod\frac{(x-y)^2}{(x+y)^2}\right\Big] }$

(راه حل :AoPS Forum - Stronger than Iran 1996's inequality • Art of Problem Solving )

2-

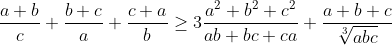
$\frac{a+b}{c}+\frac{b+c}{a}+\frac{c+a}{b}\ge 3\frac{a^2+b^2+c^2}{ab+bc+ca}+\frac{a+b+c}{\sqrt[3]{abc}}$

(راه حل : AoPS Forum - ineq • Art of Problem Solving )

3-

$(a+b)(b+c)(c+a)=8$

$\frac{5}{9\sqrt[3]{abc}}+\frac{3}{a+b+c}\ge\frac{14}{9}$

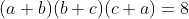
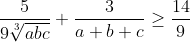
(راه حل :AoPS Forum - Inequality with (a+b)(b+c)(c+a)=8 • Art of Problem Solving )

4-

$abc=1$

$5(a+b+c)^2+39\ge 15(a+b+c)+13(ab+bc+ca)$

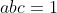
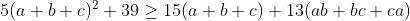
(راه حل : AoPS Forum - Inequality with abc=1 • Art of Problem Solving )

5 -

$abc=1$

$81(a^{2}+1)(b^{2}+1)(c^{2}+1)\leq{8(a+b+c)^{4}}$

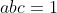
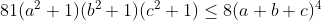
(راه حل : AoPS Forum - abc=1 • Art of Problem Solving )

6-

7-

معادلات تابعی

برای پست اول یه فایل میگذارم که خیلی معروفه و 100 تا سوال تابعی داره : AoPS Forum - 100 Functional Equations Problems (With Solutions) • Art of Problem Solving

اگر پست بعدی وجود داشته باشد !! در پست بعد خواهید دید :4: :

چند جمله ای : قضیه های مربوط به چند جمله ای و اعداد جبری .

نامساوی : روش میکسینگ و چند ایده در باره ی آن .

تابعی : بررسی چند لم کاربردی و ایده های تکراری .

خداحافظ .

math · 1393/4/1

پاسخ : .:: چند نکته در باره ی جبر در المپیاد ریاضی ::.

چند جمله ای 2 :

تحویل ناپذیری در چند جمله ای ها با ضرایب صحیح و گویا یکی از مباحثی است که کم ازش استفاده نشده و معمولا سوالاتی از این مبحث در مرحله 3 بوده . برای مثال سال پیش !

خوب همون طور که در پست اول گفتم فرض من در این تاپیک اینه که کتاب آقای صفا رو به طور نسبی خوندید و با مباحث اون آشنایی دارید برای مثال در این کتاب محک آیزنشتاین توضیح داده شده !. ( البته به دلیل نبودن یه طراح خوب در این قسمت معمولا سوالات راه حلی با همین محک داشته اند .:4: )

اول چند روش فکری که به نظرم پر کاربرد تر بوده رو میگم بعد با اضافه کردن چند محک جدید ( نسبت به ایزنشتاین جدید !) از هر کدوم چند مثال میارم .

خوب تقریبا همه ی مساله های این بخش با برهان خلف شروع میشوند و معمولا طرز فکر این طوری هستش که با برهان خلف یکسری نتیجه هایی با استفاده اتحاد ویت یا یکسری اطلاعات درباره شرایط ریشه ها و مکانشون در صفحه ی مختلط بدست میاوریم و با استفاده از شروط اولیه مساله به تناقض میرسیم . کلا توجه به ویت و مکان ریشه یه توجه پرکاربرده !!!!

یکی از قوی ترین محک ها که بسیار مورد توجه طراحان سوالاست ( البته سوال رو با این طرح میکنن ولی باز راه آیزنشتاین داره :4: .) محک پرون است که در پاببن آن را بیان کردم :

اگر چند جمله ای

$x^{n}+a_{n-1}x^{n-1}+...+a_{0}=P(x)\in \mathbb{Z}\left [ X \right ]$

و تکین باشد به طوری که ضریب ثابت آن مخالف صفر باشد و بدانیم که :

آنگاه تحویل ناپذیر است . ( باتوجه به اثبات میتوایند در حالت تساوی نامساوی بالا حرفی بزنید ؟ سعی کنید در زمان تساوی شرطی اضافه کنید که بازهم محک درست باشد . )

نکته بسیار مهم : به قسمتی که پررنگ شده بسیار توجه کنید !!

راهنمایی برای اثبات این محک : ثابت کنید دقیقا یک ریشه بیرون از دایره واحد دارد .

حالا چند سوال از این مبحث میذارم که خوب با توجه به این که میدونید که قراره پرون حل شه ( اگر هم نمیدونستید الان دیگه قطعا میدونید:4: ) دیگه راهنمایی ندارن .

سوال 1 ) فرض کنید که

$f_{1},...,f_{n}\in \mathbb{Z}\left [ X \right ]$

چند جمله ای های داده شده اند . ثابت کنید چند جمله ای تحویل پذیر

$g\in \mathbb{Z}\left [ X \right ]$

وجود دارد که

$f_{i}+g\: \: \forall 1\leq i \leq n$

تجویل ناپذیر باشد . ( سوال مرحله 3 سال 2003 ایران پس با توجه به چیزی که در بالا گفتم باید راه حل با آیزنشتاین هم داشته باشه که داره :4

سوال 2 ) فرض کنید

$f_{i}$

بیانگر i امین جمله دنباله فیبوناچی باشد . ثابت کنید چند جمله ای زیر در

$\mathbb{Z}\left [ X \right ]$

تحویل ناپذیر است .

$P(x)=x^{n}+f_{n-1}f_{n}x^{n-1}+...+f_{0}f_{1}$

( یکی از سوالای امتحانای ml بوده )

سوال 3 ) ثابت کنید چند جمله ای زیر تحویل ناپذیر است .

$P(x)=x^{n}+5x^{n-1}+3$

محک پرون تعمیم هایی هم داره که اگر مایل بودید میتونید از این جا تعمیم ها رو ببینید : http://rms.unibuc.ro/bulletin/pdf/53-3/perron.pdf

یکی دیگه از محک های (این دفعه واقعا پر قدرت ) کاربردی ( به نظر من ) محک Capelli هستش که برای بیان آن ابتدا باید چند تعریف را بیان کنیم .

تعریف اول میدان : به یک دسته ای از اعداد مانند

$\mathbb{K}$

میگویند که چند خاصیت داشته باشند :

1) جمع و ضرب و .... تعریف شود .

2) عضو خنثی در جمع و ضرب داشته باشیم

3) برای هر عضو

$\mathbb{K}$

یک عضو دیگر وجود داشته باشد که اگر باهم جمع شوند برابر عضو خنثی جمع شوند .

4) برای هر عضو

$\mathbb{K}$

یک عضو دیگر وجود داشته باشد که اگر باهم ضرب شوند برابر عضو خنثی ضرب شوند .

با توجه به تعاریف بالا به یک مجموعه مانند

$\mathbb{K}$

یک زیر میدان از

$\mathbb{C}$

میگوییم اگر تمام اعضای آن مختلط باشند و تشکیل میدان بدهند .

تعریف دوم

$\mathbb{K}\left [ \alpha \right ]$

: تمام اعدادی که بتوان چند جمله ای با ضرایب عضو

$\mathbb{K}$

پیدا کرد که در عدد

$\alpha$

مقدارشان برابر با عدد مورد نظر ما باشد .

تعریف سوم

$\mathbb{K}\left [ \alpha \right ]\left [ X \right ]$

: تمام چند جمله ای هایی است که ضرایب آن عضو

$\mathbb{K}\left [ \alpha \right ]$

باشند .

تعریف چهارم مینیمال

$\alpha$

در

$\mathbb{K}\left [ X \right ]$

: چند جمله ای تحویل ناپذیر در

$\mathbb{K}\left [ X \right ]$

که

$\alpha$

ریشه اش باشد .

محک Capelli : اگر

$\mathbb{K}$

یک زیر میدان از

$\mathbb{C}$

باشد و

$f,g\in \mathbb{K}\left [ X \right ]$

باشند به طوری که

$f$

مینیمال

$\alpha$

در

$\mathbb{K}\left [ X \right ]$

باشد و بدانیم که

$g(x)-\alpha$

در

$\mathbb{K}\left [ \alpha \right ]\left [ X \right ]$

تحویل ناپذیر است آنگاه

$f(g(x))$

در

$\mathbb{K}\left [ X \right ]$

تحویل ناپذیر است .

صورت این محک به شدت سخت و گیج کننده است ولی مساله هایی را نابود میکند که حل کردن آنها بدون این قضیه ساده نیست !

سوال 1 ) فرض کنید

$f\in \mathbb{Z}\left [ X \right ]$

یک چند جمله ای تحویل ناپذیر تکین باشد و بدانیم ضریب ثابت آن مربع کامل نیست . ثابت کنید

$g(x)=f(x^{2})$

نیز تحویل ناپذیر است .

سوال 2 ) فرض کنید

$f\in \mathbb{Z}\left [ X \right ]$

یک چند جمله ای تحویل ناپذیر تکین باشد و

$p$

یک عدد اول است . میدانیم که

$\sqrt{(-1)^{degf}f(0)}$

یک عدد گنگ شده

است . ثابت کنید

$g(x)=f(x^{p})$

تحویل ناپذیر است .

سوال 3) ثابت کنید چند جمله ای زیر تحویل ناپذیر است :

$f(x)=(x^{2}+1^{2})...(x^{2}+n^{2})+1$

سوال 4 ) ثابت کنید چند جمله ای زیر تحویل ناپذیر است :

$f(x)=(x^{2}+x)^{2^{n}}+1$

یکی دیگه از محک هایی که واقعا کاربرد داره محک osada هستش ( البته این محک به حساب نمیاد و معمولا همه به عنوان سوال ازش یاد میکنند . برای همین اسمش اصلا معروف نیست . )

محک osada ) فرض کنید p یک عدد اول باشد و میدانیم که

$p\geq \left | a_{n} \right |+....+\left | a_{1} \right |$

آنگاه ثابت کنید که چند جمله ای زیر تحویل ناپذیر است :

$f(x)=a_{n}x^{n}+...+a_{1}x+p$

سوال 1 ) برای هر عدد طبیعی مانند n ثابت کنید1+n عدد طبیعی مانند

$a_{i}$

ها وجود دارد که چند جمله ای زیر تحویل ناپذیر شود :

$f(x)=a_{n}x^{n}+...+a_{1}x+a_{0}$

سوال2 ) آیا دنباله ای از اعداد طبیعی مانند

$a_{0},a_{1},....$

وجود دارد که دو به دو نسبت به هم اول باشند و برای هر n چند جمله ای زیر تحویل ناپذیر باشد :

$f(x)=\sum_{i=1}^{n}a_{i}x^{i}$

( راهنمایی : علاوه بر محک بالا سعی کنید از چند جمله ای که از عوض کردن ضریب هایی که اندیسشان به هنگ کف نصف n یه چیز هست استفاده کنید . )

به طور کلی چند جمله ای ها در قسمت تحویل ناپذیری ایده های محدودی دارند و من سعی کردم پر کاربرد ترینشون رو ( تا جایی که من دیدم ) در بالا بیارم

نمیدونم چرا ولی نتونستم همه رو در یک پست بیارم . لطفا یکی یه پست در این تاپیک بده تا من بتونم ادامه ی قسمت دوم رو بنویسم . ( نامساوی و معادلات تابعی .)

math · 1393/6/27

پاسخ : .:: چند نکته در باره ی جبر در المپیاد ریاضی ::.

سلام !

قبل از شروع قسمت دوم ( و شاید آخر ) من یه عذر خواهی میکنم بابت این تاخیری که فکرشم نمیکردم ! این قدر زیاد باشه . قبل از شروع دوره مشکل فارسی نوشتن داشتم و بعدش هم که واقعا فرصتی نبود . به هر حال ببخشید .

و دوباره قبل از شروع یه حرفی رو بزنم که خیلی دوست داشتم بگم : چند وقت پیش با یکی از بچه های همین سایت درباره این جا صحبت میکردیم که چقدر بده و .... اینا :4:

و در نهایت من با پرسیدن یک سری سوال از چند نفر متوجه شدم که روند کاربران قسمت ریاضی ایریسک ( اکثرا رو میگم نه همه ) به این شکل هستش که اول که میان میگن چه جای خفنی ! بعدش با گذشت یه مدت میگن چه جای بدیه هیشکی توش نیست ! :4: ولی اشکال نداره من درستش میکنم ! یه کاری میکنم که همه دوباره برگردن .
و بعد از یه مدت تلاش و خستگی ! تنها چیزی که میمونه اینه که من یه درس گرفتم و اینه که آیریسک درست بشو نیست ! و اونم دیگه فعالیتی در ایریسک نداره . !

به نظرم خیلی حیفه آیریسک میتونه خیلی بهتر از اینی که هست باشه ( در قسمت ریاضی ) کاربرایی که 2-3 سال هستش که عضو هستن احتمالا یادشون میاد زمانی رو که آقای شکریان و سیفی و ملیحی و فلاح و مهر و بهزادی و حسینی و حضرتی و تجربه کار و شاولی و خدابنده و صادقی و .... ( اینا معروفاشون بودن :4: ) فعالیت داشتن
و چه قدر قسمت ریاضی فعال بود ! ( البته واقعا باید از اقای شاولی تشکر کرد چون ایشون هنوز به مرحله اخر نرسیدند و در سایت فعالیت دارند . ) یه نگاهی به این تاپیک بندازید و ببینید شباهتی بین تاپیک های اون موقع و الان میبینید ؟ http://www.irysc.com/forum/t14289/

فعالیت الان بخش ریاضی خوبه ولی باید خیلی بهتر از اینا باشه که کلا 5-6 نفر پست بدن و ...

یه مفدار زیادی حرف در این باره دارم که اگر شد آخر این قسمت مینویسم . قسمت چند جمله ای این دفعه زیاد المپیادی نیستش ( قسمت 1) ولی به نظرم خیلی خوبه که المپیاد خوندن به یاد گرفتن مباحثی که قراره توی مرحله 2 یا 3 یا انتخاب تیم و .... بیاد محدود نشه و یکم از این دوران ( که من تازه الان متوجه شدم چه قدر خوب بود !!) لذت ببرید .

قسمت دوم

چندجمله ای 1 :

می خواستم در قسمت دوم چون همون طور که گفتم ممکنه قسمت آخر هم باشه کلا از المپیاد بیام بیرون و یک سری چیز های زیبا از جبر که شاید نه شهود خوبی بده نه مساله های زیادی رو توی المپیاد حل کنه بگم ولی دیدم که عنوان تاپیک المپیاد ریاضی داره که خوب یکم به نظرم بد بود اگر این طوری میشد ! و همین طور در قسمت پیش یه سری موضوعات رو برای این قسمت گفته بودم و میخواستم اون ها رو هم در بر بگیرم ! برای همین تصمیم گرفتم هر دو رو با هم مخلوط کنم !

برای شروع این قسمت چند جمله ای ها اول یه چند جمله ای که من تا به حال توی هیچ کتاب فارسی ندیدم مستقیم توضیحش بده و خود من خیلی خیلی توی نت دنبالش بودم تا درست و حسابی بفهمم چیه و آخر هم نفهمیدم ! :4:

چند جمله ای مینیمال :

به یک عدد مانند

$\alpha$

جبری میگوییم اگر یک چند جمله ای با ضرایب صحیح یافت شود که

$\alpha$

ریشه آن باشد . ( تعریف اضافی : اگر

$\alpha$

ریشه یه چند جمله ای تکین با ضرایب صحیح باشد آنگاه به آن یک عدد صحیح جبری میگویند . )

حال بین تمام چند جمله ای هایی که

$\alpha$

ریشه ی آن هاست و ضرایبشان صحیح است چند جمله ای

$P$

را به گونه ای در نظر بگیرید که اولا ثابت صفر نباشد و ثانیا کمترین درجه را بین این چند جمله ای ها داشته باشد . به این چند جمله ای چند جمله ای مینیمال

$\alpha$

میگوییم .

این چند جمله ای چند خاصیت مهم دارد که ممکنه بسیار بدیهی باشند ولی توجه به آنها بسیار مهم است .

1) چند جمله ای مینیمال برای اعداد جبری وجود دارد و در حد ثابت یکتاست ( یعنی اگر دو چند جمله ای مینیمال یک عدد جبری باشند یکی از آنها ضریبی از دیگریست ) .

2) چند جمله ای مینیمال برای یک عدد جبری دلخواه تحویل ناپذیر است .

3) اگر

$P$

تحویل ناپذیر باشد و

$\alpha$

ریشه آن باشد انگاه

$P$

مینیمال

$\alpha$

است .

4) فرض کنید

$P$

مینیمال

$\alpha$

باشد و

$Q\in \mathbb{Z}\left [ x \right ]$

به گونه ای باشد که

$\alpha$

ریشه آن باشد اونوقت داریم که :

$P\mid Q$

. ( فوق العاده مهم است !)

خوب اثبات 4 نکته بالا بسیار سادس و به خود شما واگذار میشه . :4:

پس تا این جا تعریف چند جمله ای مینیمال و اعداد جبری رو متوجه شدیم .

تا این جا بیشتر مربوط میشد به قسمت المپیادی ماجرا حال چند تا گزاره رو بیان میکنم ( به نظرم هیجان انگیز ) و با استفاده از اون ها سعی میکنم از لم بالا یه ایده جالب رو نتیجه بگیرم !!! ( بعدا متوجه شدم این ایده توی یه قضیه نسبتا معروف استفاده شده و جدید نیست و حالم گرفته شد :4: .)

یک تابع ضربی را با دامنه و برد اعداد طبیعی در نظر بگیرید ! ( مانند

$f$

) چون تابع مساله ی ما ضربی است پس کافیه اون رو برای اعداد اول و 1 تعریف کنیم که اگر این کار را انجام بدهیم تابع بدست میاید ! ( چون ضربی است !) پس بی نهایت تابع ضربی داریم ( چون برای هر عدد اول بی نهایت گزینه داریم که مقدار تابع به ازای اون عدد اول برابر عدد مورد نظر باشد . ) . برای این که بیشتر با این موضوع آشنا بشید یک مساله رو مطرح میکنم مساله ی سختی است با یه عالمه جواب عجیب و غریب !!! ولی از نکته ی بالا به وفور !!! توش استفاده میشه !

سوال : تمام توابع پوشا مانند

$f: \mathbb{N}\rightarrow \mathbb{N}$

را بیابید به گونه ای که :

$m\mid n\Leftrightarrow f(m)\mid f(n)$

جواب های مساله : ( تمام توابع ضربی که این تابع اعداد اول را جایگشت داده است ! جواب مساله اند و فقط همین ها جوابند . )

حال یک تابع جمعی در نظر بگیرید با دامنه و برد اعداد طبیعی . برای بدست آوردن تابع کافی است مقدار تابع را در نقطه ی 1 بدست بیاریم آن وقت تابع به صورت یکتا معلوم میشود .

حال اگر یک تابع مانند

$f:\mathbb{R}\rightarrow \mathbb{R}$

در نظر بگیرید که جمعی باشد حال کافی است برای چه اعدادی مقدار f را مشخص کنیم تا تابع بدست بیاید ؟ اصلا یه همچین کاری میشه کرد ؟ میشه برای متناهی عدد مقدار f را مشخص کرد و از مقدار آنها تابع f را بدست آورد ؟

خوب برای جواب دادن به سوالات بالا یه مفهومی به اسم پایه اعداد حقیقی روی اعداد گویا تعریف میکنیم . ( برای این که این مفهوم رو به طور کامل درک کنید و فلسفه اصلی تعریف آن را بدانید میتونید علاوه بر سرچ در باره ی آن از کتاب های جبر خطی نیز میتوانید استفاده کنید ( من یه کتابی ازش دارم که مطمئن نیستم کتاب خوبی باشه برای همین نذاشتمش اگر کسی خواست بگه براش بفرستم .) ! ( کلا پایه یه مفهوم خیلی هیجان انگیزه به نظرم که توی سوالات بسیار سخت المپیادی کاربرد های فراوانی داره !)

توابع جمعی یک خاصیت مهم داشتند که در کتاب اقای صفا هم بهش اشاره شده ! و اون اینه که برای هر عدد گویا مانند c و هر عدد حقیقی مانند x داریم که :

$f(cx)=cf(x)$

که میتوان آن را با توجه به جمعی بودن تعمیم داد و تبدیل کرد به عبارت زیز :

$f(c_{1}x_{1}+...+c_{n}x_{n})=c_{1}f(x_{1})+....+c_{n}f(x_{n})$

پس اگر بتوانیم یک مجموعه ای مانند

$\mathbb{S}\subset \mathbb{R}$

را طوری در نظر بگیریم که بقیه اعدادی که عضو اعداد حقیقی هستند ولی عضو مجموعه ی

$\mathbb{S}$

نیستند را بتوان به صورت یک ترکیب خطی از اعضای

$\mathbb{S}$

نوشت که ضرایب گویا باشند کافی است مقدار f را به ازای اعدادی که عضو

$\mathbb{S}$

هستند تعیین کنیم و با توجه به عبارت بالا تابع f به صورت یکتا تعیین میشود .

به مجموعه ی

$\mathbb{S}$

پایه اعداد حقیقی روی اعداد گویا میگویند .

به شکلی دیگر میتوان پایه اعداد حقیقی را این گونه تعریف کرد مجموعه ای مانند

$\mathbb{S}$

که تمام اعداد حقیقی را میتوان به شکل ترکیب خطی هایی گویا از اعضای

$\mathbb{S}$

نوشت .

حالا یه نیمه ایده فانتزی و به نظر بدرد نخوری که آدم این جا میتونه بزنه اینه که میشه با یه تعریف خوبی ! پایه چند جمله ای برای اعداد جبری و زیر مجموعه های آن ساخت !

خوب یکی از شرط هایی که به نظر باید در این پایه چند جمله ای در نظر بگیریم این است که چند جمله ای ها ضرایب صحیح باشند ! یکی دیگه از شرط هایی که میتوان برای این اعداد گذاشت این است که ریشه های این چند جمله ای ها زیر مجموعه ای از پایه های اعداد جبری باشند . حال با توجه به لمی که بیان شد میتوان دید که این تعریف تعریف خوبی است ! و با تعریف پایه در تضاد نیست !

حال یه قضیه ای هستش که خودش خیلی قضیه ی هیجان انگیزیه ( میتونه کاربردی هم باشه !) و اثبات این قضیه با همین ایده ای است که در بالا گفته شد . یعنی با تعریف پایه چند جمله ای اعداد جبری و استفاده از قضیه های مشابه آن با پایه اعداد جبری قضیه را ثابت میکند .

قضیه : برای هر n عدد

$r_{1},...,r_{n}\in \mathbb{C}$

میتوان چند جمله ای های

$P_{1},...,P_{n}\in \mathbb{Z}\left [ X \right ]$

و عدد مختلط

$z$

را پیدا کرد که برای هر اندیس i داشته باشیم :

$P_{i}(z)=r_{i}$

( با تشکر از ارس که این قضیه رو به من گفت . )

برای دیدن یکی از سوالاتی که با استفاده از قضیه بالا حل میشود میتوانید : AoPS Forum - a hard polynomial problem • Art of Problem Solving را ببینید .

مبحث پایه اعداد حقیقی بسیار مبحث جالب و به نظرم پر کاربردی هستش که اگر قسمت سوم وجود داشت حتما به صورت جداگانه مطلبی میذارم .

با توجه به صحبت های بالا یه سوالی هستش که خیلی راه حل زیبایی داره و خیلی حیفه که بیان نشه :

سوال : آیا توابع متناوب

$f,g:\mathbb{R}\rightarrow \mathbb{R}$

وجود دارند که دوره تناوب

$f,g$

به ترتیب برابر :

$\sqrt{2}$

و

$\sqrt{3}$

باشد و دوره تناوب

$f+g$

برابر

$\sqrt{5}$

باشد ؟

(راه حل : این توابع وجود دارند ! فرض کنید هردو تابع جمعی باشند و با استفاده از پایه اعداد حقیقی روی اعداد گویا تابع را بسازید . )

نمیدونم چرا ولی نتونستم همه رو در یک پست بیارم و الان هم نمیشه چند پست پشت سر هم داد برای همین من یکی رو این جا یکی دیگه رو در پست قبلیم توی همین تاپیک گذاشتم لطفا یکی یه پست بده تا من بتونم بقیش رو هم بذارم . :3:

Farbod9717 · 1393/6/28

پاسخ : .:: چند نکته در باره ی جبر در المپیاد ریاضی ::.

على واقعا دستت درد نكنه
من كه بسيار استفاده بردم.....
خودم به شخصه خيلى علاقه دارم از اينكارو بكنم ولى نه سوادشو دارم نه قدرتشو.اگه چيزى بود كه ميتونستم كمك كنم بگو در خدمتم.
واقعيتش اين رو بايد بهت پيام ميفرستادم ولى چون يكي بايد پست ميذاشت توفيق اجبارى شد......

math · 1393/6/29

پاسخ : .:: چند نکته در باره ی جبر در المپیاد ریاضی ::.

سلام

قبل از شروع یه تشکر از فربد بخاطر پستی که داد باید بکنم . :3: ( در ضمن تو همین طوری بدون سواد طلا شدی ؟:4

خوب من وقتی این اتفاق افتاد داشتم دوباره چیزایی که در باره تابعی و نامساوی نوشته بودم رو مرور میکردم و دیدم که چه قدر لوسه !!! یعنی به نظرم بهتره خیلی با دید بازتری به المپیاد نگاه کرد . چون من توی اون چیزایی که نشوته بودم انگار دارم یه جزوه عربی مینویسم !!! برای همین سعی کردم دوباره بنویسم که خوب نشد چون فکر میکنم تابعی و نامساوی بیشتر از چند جمله ای مهارتی باشند . و بهترین کار برای قوی شدن دیدن مساله های زیاده . برای همین به جای تابعی یه قسمت چند جمله ای جدید میذارم و به جای نامساوی یکم در باره شمارا و ناشمارا بودن مینویسم که خوب نمیدونم واقعا مفید هست یا نه !

شمارا و ناشمارا :

شمارا و ناشمارا بودن برای یه دسته از اعداد تعریف میشوند . و به طور کلی یه ملاک بهتری برای مقایسه تعداد اعضای دو تا مجموعه است . مثلا اعداد طبیعی را یک دسته و اعداد گنگ را یه دسته دیگر در نظر بگیرید . میدانیم هر دو این دسته ها نامتناهی هستند . اما واقعا تعداد اعضای این دو دسته باهم برابره ؟ اصلا برای دو دسته که نامتناهی عضو دارند چه جوری برابری را تعریف کنیم ؟

مثلا وقتی میگیم دو تا چند جمله ای با هم برابرند یعنی ضریب های متناظرشون باهم برابره . حالا اگر این چند جمله ای رو تبدیل کنیم به تابع مولد ( در انتها ی کتاب اقای صفا موجوده !) که نامتناهی عضو داره حالا برابری دو تابع مولد یعنی چی ؟ (خوب اگر باهم برابر باشند یعنی تعداد ضریب ها در دو طرف برابره ) بازهم به شکل قبلی تعریف میکنیم یعنی ضریب های متناظر باهم برابر باشند . اگر یکم بیشتر دقت کنیم داریم به صورت شهودی از مفهوم متناظر بودن استفاده میکنیم . که اگر بخوایم این مفهوم رو دقیق کنیم متوجه میشیم که چرا مفهوم برابری تعداد اعضای دو مجموعه بهتره که به این شکل تعریف بشه !

میگیم تعداد اعضای دو مجموعه با هم برابر است اگر بتوانیم یک تابع یک به یک و پوشا پیدا کنیم که دامنه اش یکی از این مجموعه ها و بردش یکی دیگر باشد . با این تعریف اون برابری قدیمی ( برای متناهی عضو ) حفظ میشود اما با توجه به این تعریف هم میتوان گفت تعداد اعداد طبیعی با گنگ برابر است ؟ یعنی تابعی یک به یک و پوشا با دامنه ی اعداد گنگ و برد اعداد طبیعی وجود دارد ؟

به طور کلی مفهوم های شمارا و ناشمارا میخوان این مقایسه ها رو انجام بدن ! که کدوم مجموعه از یکی دیگه بیشتر عضو داره .

من به نظرم یه سوالی که حداقل صورتش هیجان انگیزه رو قبل از اینکه ادامه رو بخونید فکر کنید روش !

سوال : فرض کنید

$f:\mathbb{R}\rightarrow \mathbb{Q}$

است . ثابت کنید f یک به یک نیست !!

راهنمایی سوال بالا : ادامه مطلب رو بخونید !!!!!!!!

تعریف : به یک دسته از اعداد شمارا میگوییم اگر بتوان تابعی یک به یک پیدا کرد که بردش اعداد طبیعی ودامنه اش این دسته باشد . ( به زیون ساده تر این که بتونیم بشماریمش !)

و به وضوح مجموعه ای ناشماراست که این تابع وجود نداشته باشد . ( نتونیم بشماریمش )

حالا میخوایم ببینیم که چه مجموعه هایی شمارا هستند و چه مجموعه هایی ناشمارا .

خوب با توجه به تعریف بالا اولین چیزی که متوجه میشیم اینه که اعداد طبیعی شمارا هستند :4:.

حالا اگر صفر را به اعداد طبیعی اضافه کنیم چی ؟ بازهم شمارا میمونه ؟ که خوب جواب مثبت برای مثال تابع x-1 شرایط مساله رو داراست .

در باره ی اعداد صحیح چی ؟ بازهم میتوان گفت که شمارا هستند ؟ این سوال رو سعی کنید خودتون حل کنید حتما :

سوال : ثابت کنید اعداد صحیح شمارا هستند .

راهنمایی : ( اعداد منفی را به اعداد زوج و اعداد مثبت را به اعداد فرد نسبت بدهید !)

پس تا این جا متوجه شدیم که اعداد صحیح شمارا هستند پس تمام زیر مجموعه های ان نیز شمارا اند . ( اگر نبودند خود اعداد صحیح هم ناشمارا میشدند . )

حالا دسته اعداد رو بزرگ تر میکنیم . اعداد گویا چه طور ؟ این اعداد شمارا اند یا ناشمارا ؟

بازهم سعی کنید قبل از این که ادامه رو بخونید خودتون این مساله رو حل کنید چون این مساله یه راه حل خلاقانه داره اما در ادامه من یه قضیه ( نسبتا بدیهی ) رو میگم و با استفاده از اون حلش میکنم .

قضیه : اگر شمارا دسته از اعداد داشته باشیم که هر کدام شمارا عضو دارند آنگاه همه ی این اعداد تشکیل یه دسته میدهند که شمارا عضو دارد .

اثبات قضیه بالا هم خیلی شبیه اثبات شمارا بودن اعداد گویا است . راهنمایی : دسته ی اول را در خط اول دسته ی دوم را در خط دوم و .... بنویسید ( چون تعداد دسته ها شماراست میتوان این کار را انجام داد )

خوب حالا اعداد گویا همون

$\mathbb{Z}^{2}$

اند که مولفه ی اول نشان دهنده ی صورت و مولفه ی دوم نشان دهنده ی مخرج است پس با توجه به قضیه بالا و این که اعداد صحیح شمارا اند پس اعداد گویا نیز شمارا اند .

اثبات گزاره ی زیر ( به نظرمن ) فوق العاده زیباست و من توصیه میکنم قبل از خوندن راهنمایی حتما سعی کنید خودتون حلش کنید .

گزاره : اعدادی که در بازه ی باز صفر و یک هستند ناشمارا اند .

راهنمایی برای اثبات گزاره بالا : برهان خلف بزنید فرض کنید شمارا باشد . پس میتوانید یک دسته به خصوص ! از اعداد را در خط اول یک دسته بخوصوص از اعداد را در خط دوم و.... بنویسید . حال با استفاده از ارقام اعشار یک عددی بسازید که قطعا در شمارش شما نیامده است . که تناقض است.

گزاره : اعداد حقیقی ناشمارا هستند .

اثبات گزاره ی بالا بدیهی است چون ثابت کردیم یک زیر مجموعه ای از ان نا شماراست پس خودش نیز ناشمارا هست .

حال با توجه به توضیحات بالا سعی کنید سوال زیر را حل کنید: ( یکی از سوالای خلاقیت امسال ! )

سوال : میگوییم اگر یا اگر

$a=d$

آنگاه باشد .

آیا تابعی یک به یک و پوشا و صعودی با دامنه ی

$\mathbb{R}^{2}$

و برد

$\mathbb{R}$

وجود دارد ؟

(راهنمایی : فرض کنید وجود داشته باشد این خطوط بدست آمده از تابع را روی محور تصویر کنید به وضوع یک سری بازه میشود . اما تعداد این بازه ها باید ناشمارا باشد اما چون تابع صعودی است پس این بازه ها اشتراک ندارند و چون در هر بازه ای یک عدد گویا وجود دارد پس شمارا است که تناقض است . !!)

حال با توجه به اطلاعات بالا سوالی که قبل از شروع مبحث شمارا و ناشمارا نوشته بودم بدیهی است چون اعداد حقیقی شمارا اند و اعداد گویا شمارا پس تابع یک به یک نیست .

با توجه به ایده ی مساله ی بالا سوال پایین هم میتونه یه سوال هیجان انگیز باشه . ( سوال خلاقیت امسال !)

سوال : میدانیم که

$P\in \mathbb{R}\left [ X \right ]$

چند جمله ای تکین با درجه ی فرد است و

$f:\mathbb{R}\rightarrow \mathbb{Z}$

تابعی ای است که برای هر عدد حقیقی داریم :

$f(p(x))=p(f(x))$

ثابت کنید برد تابع متناهی است .

( نکته جالب این جاست که اگر هر کدوم از شرط ها رو تغییر بدیم یا برداریم تابعی وجود داره که بردش نامتناهی بشه !)

بازهم یه سوال دیگه که ایده اصلیش اینه که : شمارا تا شمارا میشه شمارا !!!!!!

سوال : آیا میتوان ناشمارا تا دایره مجزا از هم در صفحه رسم کرد ؟

راهنمایی : چون شمارا تا شمارا شمارا میشود پس

$\mathbb{Q}^{2}$

شماراست اما در هر دایره حداقل یه نقطه با مختصات گویا وجود دارد .

با استفاده از سوال بالا آقای ملیحی راه حلی برای یک سوال تابعی نوشتن که به نظر من فوق العادس . توصیه میکنم قبل از این که راه حل رو بخونید حتما حتما با سوال بالا بهش فکر کنید .

f(x)f(y)<=|x-y

در آخر یه سوال خیلی مهیج ( حداقل برای من ) رو که آقای ثقفیان روز سوم دوره بود فکر کنم دادن که بی ربط نیست به این موضوع رو مینویسم به طور کلی خیلی سخته و اصلا یه قضیه هستش ولی به نظرم راهش دوراز ذهن هم نیست و همچنین یکی دیگه از سوال های خلاقیت که اونم بی شباهت نیستش به بحث های این پست رو میذارم

سوال : فرض کنید تابعی یک به یک از مجموعه ی

$A$

به مجموعه ی

$B$

وجود دارد . و تابعی یک به یک از مجموعه ی

$B$

به مجموعه ی

$A$

وجود دارد . ثابت کنید تابعی یک

به یک و پوشا از مجموعه ی

$A$

به مجموعه ی

$B$

وجود دارد .

سوال : ( خلاقیت امسال ) ایا گزاره ی زیر درست است ؟

اگر تابعی با دامنه ی

$A$

و برد

$B$

وجود داشته باشد که صعودی و پوشا باشد آنگاه لزوما تابعی یک به یک و صعودی و پوشا با دامنه ی

$A$

و برد

$B$

وجود دارد .

بازهم به دلیل همون مشکل قبلی نمیتونم قسمت سوم چند جمله ای رو بزارم لطفا باهم یکی یه پست بزاره .:4:

Farbod9717 · 1393/6/30

پاسخ : .:: چند نکته در باره ی جبر در المپیاد ریاضی ::.

باز من باید پست بدم مثکه!!میترسم بخاطر اسپک بنم کنید!!!:4:
اون سوال r به r[sup]2[/sup]فقط واسه من مشکل داره که نمیاد؟!!
حالا یه نکته جالب اینکه من یکی از معدود مباحثی که واسه خلاقیت خوندم همین شمارا ناشمارا بود ولی هیچی سوال باهاش حل نکردم.:4:
اون سوال تابعی که گذاشتی(فک کنم سوال خلاقیت چند سال پیش بوده)راه دیگه ای جز شمارا ناشمارا داره؟!

حمید آنالیز · 1394/2/6

پاسخ : .:: چند نکته در باره ی جبر در المپیاد ریاضی ::.

آقا میشه یکم هم ادامه بدیم خیلی تاپیک جالبیه درباره انواع نامساوی و تکنیکاشون.ممنون:4:

yeganeh1383 · 1399/3/5

عالی

.:: چند نکته در باره ی جبر در المپیاد ریاضی ::.

math

New Member

math

New Member

math

New Member

Farbod9717

New Member

math

New Member

Farbod9717

New Member

حمید آنالیز

Well-Known Member

yeganeh1383

New Member