f(x,y)=f(y,x), 1-1
پاسخ : f(x,y)=f(y,x), 1-1
نه. ثابت میشه که عدد
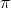 شامل هر رشته ای از اعداد در ارقام اعشاری اش است. پس کافیه یک جا سه تا رقم صفر پشت سر هم داشته باشه تا مثال شما نادرست بشه.
شامل هر رشته ای از اعداد در ارقام اعشاری اش است. پس کافیه یک جا سه تا رقم صفر پشت سر هم داشته باشه تا مثال شما نادرست بشه.
برای این سوال، می دونیم که اعداد گویا در تناظر یک به یک با این مجموعه است، و اعداد گویا هم در تناظر یک به یک با اعداد طبیعی است، پس حتما چنین تابعی وجود دارد.
این نمیشه؟
پی تا x رقم اعشار + پی تا y رقم اعشار
پی تا x رقم اعشار + پی تا y رقم اعشار
برای این سوال، می دونیم که اعداد گویا در تناظر یک به یک با این مجموعه است، و اعداد گویا هم در تناظر یک به یک با اعداد طبیعی است، پس حتما چنین تابعی وجود دارد.
پاسخ : f(x,y)=f(y,x), 1-1
---- دو نوشته به هم متصل شده است ----
برد این توابع اعداد طبیعی نیستند.
ru soal ham nagofte ke baiad bord ham adadetabii bashe faghat X,Y tabiye
---- دو نوشته به هم متصل شده است ----
xob age aslan bexaym tabii bashe ham in karo mikonim f(x,y)=((10^(x+y)-1)/9)*10^(|x-y|+1)+(10^(|x-y|+1)-1)*2/9 :35:
dar vaghebe tedade x+y ragham 1 dar ebteda va be tedade |x-y|+1 ragham ham 2 dar axare adad
x=1,y=2 :x+y=3 |x-y|+1=2 => f(x,y)=11122
dar vaghebe tedade x+y ragham 1 dar ebteda va be tedade |x-y|+1 ragham ham 2 dar axare adad
x=1,y=2 :x+y=3 |x-y|+1=2 => f(x,y)=11122
