.::ماراتن 4 درس ::.
پاسخ : .::ماراتن 4 درس ::.
سوالای ماراتن:

و

نشان دهید

(2 جبر)فرض کنید
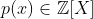 و دارای n ریشه صحیح متمایز باشد . ثابت کنید
و دارای n ریشه صحیح متمایز باشد . ثابت کنید
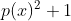 عاملی با درجه دست کم
عاملی با درجه دست کم
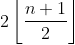 دارد که در
دارد که در
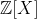 تحویل ناپذیر است .
تحویل ناپذیر است .
(1 نظریه) تعداد چهار تایی های x,y,z,w را از اعداد حسابی بیابید x,y,z,w کوچکترمساوی 36
و
x[SUP]2[/SUP]+y[SUP]2[/SUP]به همنهشت 37 برابر با z[SUP]3[/SUP]+w[SUP]3[/SUP]
باشد
راهنمایی(جواب عدد کوچکی نیست)
(2 نظریه)ثابت کنید در بسط اعشاری
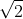 بین رقم یک میلیونیم تا 3 میلینیم حداقل یک رقم ناصفر وجود دارد .
بین رقم یک میلیونیم تا 3 میلینیم حداقل یک رقم ناصفر وجود دارد .
(2 هندسه)
 وسط
وسط
 از مثلث
از مثلث
 است و داریم :
است و داریم :
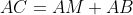 . دایره محاطی مثلث میانه
. دایره محاطی مثلث میانه
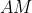 را در
را در
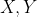 قطع میکند . نشان دهید
قطع میکند . نشان دهید
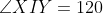
(1 هندسه) در مثلث abc از h دو خط عمود برهم
میکشیم تا abوac را درeوf قطع کند.
ef دایره به قطر bc را درm قطع کند.
نشان دهید cm موازی he است.
(1 ترکیبیات)
فردی دور یک دایره به محیط یک راه میرودبا طول قدم
 که عددی گنگ است
که عددی گنگ است
روی این دایره گودالی به قطر
 داریم ثابت کنید قطر گودال هر چه کوچک باشد شخص در آن میافتد
داریم ثابت کنید قطر گودال هر چه کوچک باشد شخص در آن میافتد
بیانی دیگر
ثابت کنید برای هر عدد گنگ
 و عدد حقیقی ومثبت
و عدد حقیقی ومثبت
 عدد طبیعی
عدد طبیعی
 موجود است که
موجود است که
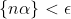
ب) به مرکز هریک از نقاط شبکه ای دایره ای به شعاع
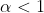 رده ایم
رده ایم
ثابت کنید مثلث متساوی الاضلاعی داریم که رووسش داخل این دایره ها باشند
(2 ترکیبیات)اعداد
 تا
تا
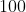 در یک جدول10*10 چیده شده اند
در یک جدول10*10 چیده شده اند
در هر مرحله میتوانیم جای هر دو عددی را که میخواهیم با هم عوض کنیم
ثابت کنید میتوان
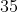 حرکت انجام داد به گونه ای که مجموع اعداد واقع در خانه های مجاور عددی مرکب باشد
حرکت انجام داد به گونه ای که مجموع اعداد واقع در خانه های مجاور عددی مرکب باشد
لطفا هر کسی سوال میذاره همین پست رو نقل قول کنه
مواردش رو کپی کنه سوالش رو هم تو جاش جایگزین کنه
ممنون
سوالای ماراتن:
(1 جبر)
اگر

و

نشان دهید

(2 جبر)فرض کنید
(1 نظریه) تعداد چهار تایی های x,y,z,w را از اعداد حسابی بیابید x,y,z,w کوچکترمساوی 36
و
x[SUP]2[/SUP]+y[SUP]2[/SUP]به همنهشت 37 برابر با z[SUP]3[/SUP]+w[SUP]3[/SUP]
باشد
راهنمایی(جواب عدد کوچکی نیست)
(2 نظریه)ثابت کنید در بسط اعشاری
(2 هندسه)
(1 هندسه) در مثلث abc از h دو خط عمود برهم
میکشیم تا abوac را درeوf قطع کند.
ef دایره به قطر bc را درm قطع کند.
نشان دهید cm موازی he است.
(1 ترکیبیات)
مربعی به ضلع 1 داریم
مثلثی درون آن است که مرکز مربع خارج آن است.
ثابت کنید ضلعی از مثلث کمتر از 1 است.
به علت هماهنگ نبودن من الان دوتا از این سطح داریم
اینم دومین ترکیبیات 1:
یه سوال خیلی کلاسیک و قدیمیمثلثی درون آن است که مرکز مربع خارج آن است.
ثابت کنید ضلعی از مثلث کمتر از 1 است.
به علت هماهنگ نبودن من الان دوتا از این سطح داریم
اینم دومین ترکیبیات 1:
فردی دور یک دایره به محیط یک راه میرودبا طول قدم
روی این دایره گودالی به قطر
بیانی دیگر
ثابت کنید برای هر عدد گنگ
ب) به مرکز هریک از نقاط شبکه ای دایره ای به شعاع
ثابت کنید مثلث متساوی الاضلاعی داریم که رووسش داخل این دایره ها باشند
(2 ترکیبیات)
در هر مرحله میتوانیم جای هر دو عددی را که میخواهیم با هم عوض کنیم
ثابت کنید میتوان
لطفا هر کسی سوال میذاره همین پست رو نقل قول کنه
مواردش رو کپی کنه سوالش رو هم تو جاش جایگزین کنه
ممنون
پاسخ : .::ماراتن 4 درس ::.
برای یک جبر
درابتدا همه اعداد را برابر با توان 2 عددی دیگر بگیرید(یعنی a =x[SUP]2[/SUP]
(
سپس تابع محدب بسازید
حال باید ثابت کنید : x[SUP]2[/SUP]y[SUP]2[/SUP]+x[SUP]2[/SUP]z[SUP]2[/SUP]+y[SUP]2[/SUP]z[SUP]2[/SUP]+3 از x+y+z کوچکتر است
که این با لاگرانژ ثابت می شود
اگه درسته سوال جدید بذارم
برای یک جبر
درابتدا همه اعداد را برابر با توان 2 عددی دیگر بگیرید(یعنی a =x[SUP]2[/SUP]
(
سپس تابع محدب بسازید
حال باید ثابت کنید : x[SUP]2[/SUP]y[SUP]2[/SUP]+x[SUP]2[/SUP]z[SUP]2[/SUP]+y[SUP]2[/SUP]z[SUP]2[/SUP]+3 از x+y+z کوچکتر است
که این با لاگرانژ ثابت می شود
اگه درسته سوال جدید بذارم
پاسخ : .::ماراتن 4 درس ::.
از اینکه

چه استفاده ای میکنی؟
بله هرسوال نامساوی با لاگرانژ حل میشه ولی راه حل خلاقیتی مهم است.
اگر میشه راهی به جز لاگرانژ پیشنهاد بدید.
به نظر من این راه هیچ ارزشی ندارد.
برای یک جبر
درابتدا همه اعداد را برابر با توان 2 عددی دیگر بگیرید(یعنی a =x[SUP]2[/SUP]
(
سپس تابع محدب بسازید
حال باید ثابت کنید : x[SUP]2[/SUP]y[SUP]2[/SUP]+x[SUP]2[/SUP]z[SUP]2[/SUP]+y[SUP]2[/SUP]z[SUP]2[/SUP]+3 از x+y+z کوچکتر است
که این با لاگرانژ ثابت می شود
اگه درسته سوال جدید بذارم
درابتدا همه اعداد را برابر با توان 2 عددی دیگر بگیرید(یعنی a =x[SUP]2[/SUP]
(
سپس تابع محدب بسازید
حال باید ثابت کنید : x[SUP]2[/SUP]y[SUP]2[/SUP]+x[SUP]2[/SUP]z[SUP]2[/SUP]+y[SUP]2[/SUP]z[SUP]2[/SUP]+3 از x+y+z کوچکتر است
که این با لاگرانژ ثابت می شود
اگه درسته سوال جدید بذارم

چه استفاده ای میکنی؟
بله هرسوال نامساوی با لاگرانژ حل میشه ولی راه حل خلاقیتی مهم است.
اگر میشه راهی به جز لاگرانژ پیشنهاد بدید.
به نظر من این راه هیچ ارزشی ندارد.
پاسخ : .::ماراتن 4 درس ::.
البته ( این نظر شخصی منه ) حل سوال با سواد و کم یا نبودن خلاقیت هیچ کم از راه حل خلاقانه که ندارد هیچ شاید بالا تر هم باشد
و یه نکته دیگه این که تمام نامساوی ها با لاگرانژ حل نمیشه
بهتره هر سوال رو با سواد سطحش حل کنیم اگر این سوال سطح دو بود راه حل ایشون کاملا درست و ... بود اما این سوال در سطح یک اورده شده پس باید با سواد مرحله حل شود
البته ( این نظر شخصی منه ) حل سوال با سواد و کم یا نبودن خلاقیت هیچ کم از راه حل خلاقانه که ندارد هیچ شاید بالا تر هم باشد
و یه نکته دیگه این که تمام نامساوی ها با لاگرانژ حل نمیشه
بهتره هر سوال رو با سواد سطحش حل کنیم اگر این سوال سطح دو بود راه حل ایشون کاملا درست و ... بود اما این سوال در سطح یک اورده شده پس باید با سواد مرحله حل شود
پاسخ : .::ماراتن 4 درس ::.
هرکسی نظری داره.
البته ( این نظر شخصی منه ) حل سوال با سواد و کم یا نبودن خلاقیت هیچ کم از راه حل خلاقانه که ندارد هیچ شاید بالا تر هم باشد
و یه نکته دیگه این که تمام نامساوی ها با لاگرانژ حل نمیشه
بهتره هر سوال رو با سواد سطحش حل کنیم اگر این سوال سطح دو بود راه حل ایشون کاملا درست و ... بود اما این سوال در سطح یک اورده شده پس باید با سواد مرحله حل شود
و یه نکته دیگه این که تمام نامساوی ها با لاگرانژ حل نمیشه
بهتره هر سوال رو با سواد سطحش حل کنیم اگر این سوال سطح دو بود راه حل ایشون کاملا درست و ... بود اما این سوال در سطح یک اورده شده پس باید با سواد مرحله حل شود
پاسخ : .::ماراتن 4 درس ::.
خوب این شرط تو لاگرانژ استفاده میشه دیگه
اگه با یه راه دیگه بلدی اسم نامساوی که استفاده کردی رو بگو تا با همون حل کنم (به عنوان راهنمایی بگو)
:176::176::176:
اگه با یه راه دیگه بلدی اسم نامساوی که استفاده کردی رو بگو تا با همون حل کنم (به عنوان راهنمایی بگو)
:176::176::176:
پاسخ : .::ماراتن 4 درس ::.
سوال سطح 1 نظریه اعداد یعنی سوال سطح مرحله 2 نه مرحله 1 
من سوال دیگه ای میذارم :
ثابت کنید در دنباله ی زیر بی نهایت عامل اول وجود دارد
 ( بدون استفاده از قضیه کوبایاشی البته
( بدون استفاده از قضیه کوبایاشی البته  )
)
(1 نظریه) تعداد چهار تایی های x,y,z,w را از اعداد حسابی بیابید x,y,z,w کوچکترمساوی 36
و
x[SUP]2[/SUP]+y[SUP]2[/SUP]به همنهشت 37 برابر با z[SUP]3[/SUP]+w[SUP]3[/SUP]
باشد
و
x[SUP]2[/SUP]+y[SUP]2[/SUP]به همنهشت 37 برابر با z[SUP]3[/SUP]+w[SUP]3[/SUP]
باشد
من سوال دیگه ای میذارم :
ثابت کنید در دنباله ی زیر بی نهایت عامل اول وجود دارد
آخرین ویرایش توسط مدیر
پاسخ : .::ماراتن 4 درس ::.
شما به این سوال مطمینید؟؟؟
اگر m که مقدار ثابت هست رو برابر 1 فرض کنیم اوننوقت باید ثابت کنیم بینهایت عدد اول فرما داریم؟؟؟
که هنوز ثابت نشده؟؟؟
آیا من در اشتباهم؟؟؟
سوال سطح 1 نظریه اعداد یعنی سوال سطح مرحله 2 نه مرحله 1 
من سوال دیگه ای میذارم :
ثابت کنید در دنباله ی زیر بی نهایت عامل اول وجود دارد
 ( بدون استفاده از قضیه کوبایاشی البته
( بدون استفاده از قضیه کوبایاشی البته  )
)
من سوال دیگه ای میذارم :
ثابت کنید در دنباله ی زیر بی نهایت عامل اول وجود دارد
اگر m که مقدار ثابت هست رو برابر 1 فرض کنیم اوننوقت باید ثابت کنیم بینهایت عدد اول فرما داریم؟؟؟
که هنوز ثابت نشده؟؟؟
آیا من در اشتباهم؟؟؟
پاسخ : .::ماراتن 4 درس ::.
سوال نگفته که بی نهایت عدد اول توی این دنباله هست گفته بی نهایت عامل اول هست یعنی بی نهایت عدد اول وجود دارد که یکی از اعضای دنباله بر ان بخش پذیر شود
شما به این سوال مطمینید؟؟؟
اگر m که مقدار ثابت هست رو برابر 1 فرض کنیم اوننوقت باید ثابت کنیم بینهایت عدد اول فرما داریم؟؟؟
که هنوز ثابت نشده؟؟؟
آیا من در اشتباهم؟؟؟
اگر m که مقدار ثابت هست رو برابر 1 فرض کنیم اوننوقت باید ثابت کنیم بینهایت عدد اول فرما داریم؟؟؟
که هنوز ثابت نشده؟؟؟
آیا من در اشتباهم؟؟؟
سوال نگفته که بی نهایت عدد اول توی این دنباله هست گفته بی نهایت عامل اول هست یعنی بی نهایت عدد اول وجود دارد که یکی از اعضای دنباله بر ان بخش پذیر شود
پاسخ : .::ماراتن 4 درس ::.
سوالی که گذاشتم مال ترکیه بوده بعد تازه نیاز به دقت خیلی زیادی داره اگه واقعا آسونه پس جواب دقیقش رو بنویس(فرض کن همین سوال 1 مرحله 2 باشه )
سوال سطح 1 نظریه اعداد یعنی سوال سطح مرحله 2 نه مرحله 1 
من سوال دیگه ای میذارم :
ثابت کنید در دنباله ی زیر بی نهایت عامل اول وجود دارد
 ( بدون استفاده از قضیه کوبایاشی البته
( بدون استفاده از قضیه کوبایاشی البته  )
)
من سوال دیگه ای میذارم :
ثابت کنید در دنباله ی زیر بی نهایت عامل اول وجود دارد
سوالی که گذاشتم مال ترکیه بوده بعد تازه نیاز به دقت خیلی زیادی داره اگه واقعا آسونه پس جواب دقیقش رو بنویس(فرض کن همین سوال 1 مرحله 2 باشه )
پاسخ : .::ماراتن 4 درس ::.
ببخشید من بلد نبودم حساب کنم سوال جدید گذاشتم ولی یک چیزی این سوال سبک مرحله 2 ای نداره :1:
سطح 2 (مرحله 3 )
فرض کنید
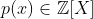 و دارای n ریشه صحیح متمایز باشد . ثابت کنید
و دارای n ریشه صحیح متمایز باشد . ثابت کنید
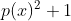 عاملی با درجه دست کم
عاملی با درجه دست کم
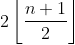 دارد که در
دارد که در
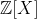 تحویل ناپذیر است .
خوب مثل اینکه جبر کاری نداشتیم که سوال 2 رو حل کنه من راه حلش رو میزارم :
تحویل ناپذیر است .
خوب مثل اینکه جبر کاری نداشتیم که سوال 2 رو حل کنه من راه حلش رو میزارم :
فرض کنید
 دارای k عامل باشد پس داریم :
دارای k عامل باشد پس داریم :

حال به وضوح درجه S ها زوج است
حال فرض کنید ریشه ها
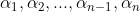 باشد پس به وضوح داریم :
باشد پس به وضوح داریم :

حال اگر از رابطه ی اول مشتق بگیرید و به این نکته توجه کنید که :
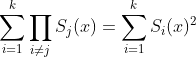
حال اگر جای x ریشه ها را بگذاریم میدانیم :

پس معقول هست که چند جمله ایه روبرو را در نظر بگیریم :
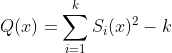
حال میدانیم :
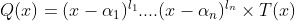
که در ان
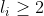 پس حداقل یکی از S ها در جه بزرگ تر از
پس حداقل یکی از S ها در جه بزرگ تر از
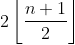 دارد ( در دو حالت زوج و فرد بررسی کنید و برهان خلف بزنید )
دارد ( در دو حالت زوج و فرد بررسی کنید و برهان خلف بزنید )
سوال جدید هم تا شب میزارم ببخشید
سوالی که گذاشتم مال ترکیه بوده بعد تازه نیاز به دقت خیلی زیادی داره اگه واقعا آسونه پس جواب دقیقش رو بنویس(فرض کن همین سوال 1 مرحله 2 باشه )
ببخشید من بلد نبودم حساب کنم سوال جدید گذاشتم ولی یک چیزی این سوال سبک مرحله 2 ای نداره :1:
سطح 2 (مرحله 3 )
فرض کنید
فرض کنید
حال فرض کنید ریشه ها
حال اگر جای x ریشه ها را بگذاریم میدانیم :
سوال جدید هم تا شب میزارم ببخشید
پاسخ : .::ماراتن 4 درس ::.
سوالای ماراتن:

و

نشان دهید

(2 جبر)نداریم!
(1 نظریه) ثابت کنید در دنباله ی زیر بی نهایت عامل اول وجود دارد
 ( بدون استفاده از قضیه کوبایاشی البته
( بدون استفاده از قضیه کوبایاشی البته  )
)
(2 نظریه)ثابت کنید در بسط اعشاری
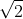 بین رقم یک میلیونیم تا 3 میلینیم حداقل یک رقم ناصفر وجود دارد .
بین رقم یک میلیونیم تا 3 میلینیم حداقل یک رقم ناصفر وجود دارد .
(2 هندسه)
 وسط
وسط
 از مثلث
از مثلث
 است و داریم :
است و داریم :
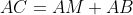 . دایره محاطی مثلث میانه
. دایره محاطی مثلث میانه
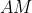 را در
را در
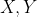 قطع میکند . نشان دهید
قطع میکند . نشان دهید
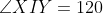
(1 هندسه) در مثلث abc از h دو خط عمود برهم
میکشیم تا abوac را درeوf قطع کند.
ef دایره به قطر bc را درm قطع کند.
نشان دهید cm موازی he است.
(1 ترکیبیات)
 که عددی گنگ است
که عددی گنگ است
روی این دایره گودالی به قطر
 داریم ثابت کنید قطر گودال هر چه کوچک باشد شخص در آن میافتد
داریم ثابت کنید قطر گودال هر چه کوچک باشد شخص در آن میافتد
بیانی دیگر
ثابت کنید برای هر عدد گنگ
 و عدد حقیقی ومثبت
و عدد حقیقی ومثبت
 عدد طبیعی
عدد طبیعی
 موجود است که
موجود است که
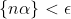
ب) به مرکز هریک از نقاط شبکه ای دایره ای به شعاع
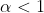 رده ایم
رده ایم
ثابت کنید مثلث متساوی الاضلاعی داریم که رووسش داخل این دایره ها باشند)
جواب:
پاره خطی به طول
 رو در نظر بگیرید.
رو در نظر بگیرید.
اگر از وسطش یه عمود به طول
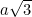 خارج کنیم راس سوم مثلث متساوی الاضلاع بدست می آید
خارج کنیم راس سوم مثلث متساوی الاضلاع بدست می آید
حالا طبق بخش الف میدانیم
 ای داریم که
ای داریم که
 پس راس سوم داخل یکی از دایره ها واقع میشود
پس راس سوم داخل یکی از دایره ها واقع میشود
سوال جایگزینش هم که از قبل وجود داشت
حالا هم جواب سوال دوم اعداد
اعداد
 تا
تا
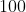 در یک جدول10*10 چیده شده اند
در یک جدول10*10 چیده شده اند
در هر مرحله میتوانیم جای هر دو عددی را که میخواهیم با هم عوض کنیم
ثابت کنید میتوان
 حرکت انجام داد به گونه ای که مجموع اعداد واقع در خانه های مجاور عددی مرکب باشد)
حرکت انجام داد به گونه ای که مجموع اعداد واقع در خانه های مجاور عددی مرکب باشد)
جواب:جدول رو از وسط تا میکنیم تا دوتا جدول 5*10 به وجود بیاد
تو یکی از این جدول ها تعداد اعداد فرد کمتره
عدد های فرد این جدول رو با اعداد زوج جدول دیگری عوض کنید
حداکثر 25 حرکت لازمه
حالا مرز بین دو جدول دیگه جمع اعدادش زوج نیست
میتونیم با 10 حرکت (هر خونه یکبار )کاری بکنیم که مجموع خونه های مجاور مضرب3 بشود و به وضوح مضرب سه به تعداد کافی داریم
سوال جایگزین رو تو سوالای مراتن گذاشتم
سوالای ماراتن:
(1 جبر)
اگر

و

نشان دهید

(2 جبر)نداریم!
(1 نظریه) ثابت کنید در دنباله ی زیر بی نهایت عامل اول وجود دارد
(2 نظریه)ثابت کنید در بسط اعشاری
(2 هندسه)
(1 هندسه) در مثلث abc از h دو خط عمود برهم
میکشیم تا abوac را درeوf قطع کند.
ef دایره به قطر bc را درm قطع کند.
نشان دهید cm موازی he است.
(1 ترکیبیات)
مربعی به ضلع 1 داریم
مثلثی درون آن است که مرکز مربع خارج آن است.
ثابت کنید ضلعی از مثلث کمتر از 1 است.
(2 ترکیبیات)
یک جدول 2013*1392 داریم که بیش از 2011*1390 خانه ی آن سفیدندمثلثی درون آن است که مرکز مربع خارج آن است.
ثابت کنید ضلعی از مثلث کمتر از 1 است.
(2 ترکیبیات)
در هر مرحله میتوانیم یک جدول 2*2 از آن را که سه خانه ی سیاه دارد در نظر بگیریم و خانه ی چهارم رو هم سیاه کنیم
ثابت کنید با انجام این عمل نمیتوان همه ی خانه های جدول را سیاه کرد.
لطفا هر کسی سوال میذاره همین پست رو نقل قول کنه
مواردش رو کپی کنه سوالش رو هم تو جاش جایگزین کنه
ممنون
من از جناب math درخواست دارم جواب سوال سطح 2 نظریه رو هم بذارن
منم جواب سوال ترکیبیات هایی که خودم گذاشتم رو میذارم
سوال اول یه سوال خیلی کلاسیک و قدیمی
یه سوال خیلی کلاسیک و قدیمی
فردی دور یک دایره به محیط یک راه میرودبا طول قدم
ثابت کنید با انجام این عمل نمیتوان همه ی خانه های جدول را سیاه کرد.
لطفا هر کسی سوال میذاره همین پست رو نقل قول کنه
مواردش رو کپی کنه سوالش رو هم تو جاش جایگزین کنه
ممنون
من از جناب math درخواست دارم جواب سوال سطح 2 نظریه رو هم بذارن
منم جواب سوال ترکیبیات هایی که خودم گذاشتم رو میذارم
سوال اول
روی این دایره گودالی به قطر
بیانی دیگر
ثابت کنید برای هر عدد گنگ
ب) به مرکز هریک از نقاط شبکه ای دایره ای به شعاع
ثابت کنید مثلث متساوی الاضلاعی داریم که رووسش داخل این دایره ها باشند)
جواب:
پاره خطی به طول
اگر از وسطش یه عمود به طول
حالا طبق بخش الف میدانیم
سوال جایگزینش هم که از قبل وجود داشت
حالا هم جواب سوال دوم
در هر مرحله میتوانیم جای هر دو عددی را که میخواهیم با هم عوض کنیم
ثابت کنید میتوان
جواب:جدول رو از وسط تا میکنیم تا دوتا جدول 5*10 به وجود بیاد
تو یکی از این جدول ها تعداد اعداد فرد کمتره
عدد های فرد این جدول رو با اعداد زوج جدول دیگری عوض کنید
حداکثر 25 حرکت لازمه
حالا مرز بین دو جدول دیگه جمع اعدادش زوج نیست
میتونیم با 10 حرکت (هر خونه یکبار )کاری بکنیم که مجموع خونه های مجاور مضرب3 بشود و به وضوح مضرب سه به تعداد کافی داریم
سوال جایگزین رو تو سوالای مراتن گذاشتم
پاسخ : .::ماراتن 4 درس ::.
حرف شما رو قبول دارم
این یکی از اشکالات ماراتن هاست که ممکنه برای بعضیها سوالی رو بسوزونه
ولی خوب وقتی چند نفر به مدت چند روز روی یه سوال فکر میکنن و به نتیجه ی قابل قبولی نمیرسن باید جوابش رو گذاشت
شما هم اگه اخساس میکنین روی سوال کمتر از اندازه ای که باید فکر کردین خوب برید کامل روش فکر کنید و بعدا برگردید و جواب کاملش رو بخونید
لازم نیست که هرکی جواب رو گذاشت شما هم همون موقع جواب رو بخونید
یعنی قشنگ همه ثابت کنیده
جای من نیست اینجا
جای من نیست اینجا
این یکی از اشکالات ماراتن هاست که ممکنه برای بعضیها سوالی رو بسوزونه
ولی خوب وقتی چند نفر به مدت چند روز روی یه سوال فکر میکنن و به نتیجه ی قابل قبولی نمیرسن باید جوابش رو گذاشت
شما هم اگه اخساس میکنین روی سوال کمتر از اندازه ای که باید فکر کردین خوب برید کامل روش فکر کنید و بعدا برگردید و جواب کاملش رو بخونید
لازم نیست که هرکی جواب رو گذاشت شما هم همون موقع جواب رو بخونید
