سوال 1:
نشان دهید برای هر
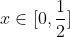 نامساوی
نامساوی
 برقرار است.
برقرار است.
سوال 2:
نمودار تابع
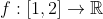 با ضابطه ی
با ضابطه ی
 را حول محور
را حول محور
 ها دوران می دهیم. حجم ناحیه ی تولید شده را به دست آورید.
ها دوران می دهیم. حجم ناحیه ی تولید شده را به دست آورید.
سوال 3:
مقدار
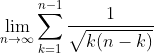 را با ذکر دلیل محاسبه کنید.
را با ذکر دلیل محاسبه کنید.
سوال 4:
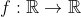 یک تابع مشتق پذیر با مشتق پیوسته است به طوری که
یک تابع مشتق پذیر با مشتق پیوسته است به طوری که
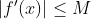 برای هر
برای هر
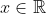 . ثابت کنید:
. ثابت کنید:
الف) اگر برای
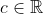 داشته باشیم
داشته باشیم
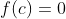 آنگاه برای هر
آنگاه برای هر
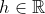 داریم:
داریم:
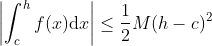 ب) اگر برای
ب) اگر برای
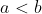 داشته باشیم
داشته باشیم
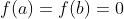 ، آنگاه
، آنگاه
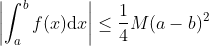 سوال 5:
سوال 5:
شعاع همگرایی سری توانی
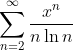 با متغیر حقیقی
با متغیر حقیقی
 را محاسبه کنید و همگرایی آن را در نقاط ابتدایی و انتهایی بازه ی همگرایی بررسی کنید.
را محاسبه کنید و همگرایی آن را در نقاط ابتدایی و انتهایی بازه ی همگرایی بررسی کنید.
سوال 6:
تابع
 را در نظر می گیریم.
را در نظر می گیریم.
الف) مشتق
 را محاسبه کنید.
را محاسبه کنید.
ب) نشان دهید
 .
.
نشان دهید برای هر
سوال 2:
نمودار تابع
سوال 3:
مقدار
سوال 4:
الف) اگر برای
شعاع همگرایی سری توانی
سوال 6:
تابع
الف) مشتق
ب) نشان دهید
آخرین ویرایش توسط مدیر
