ماراتن هندسه version 2
- ارسال ها
- 935
- لایک ها
- 1,654
- امتیاز
- 93
پاسخ : ماراتن هندسه version 2
پای عمود A_1 بر AC و AB رو به ترتیب S و Q می نامیم . و پای عمود B_1 بر AB , BC رو به ترتیب P و R می نامیم .
چهارضلعی
 محاطی است پس
محاطی است پس

چهارضلعی
 محاطی است پس
محاطی است پس
 پس SP موازی است با RQ . حالا فقط باید ثابت کنیم که RS = PQ.
پس SP موازی است با RQ . حالا فقط باید ثابت کنیم که RS = PQ.
حالا میایم RB_1 , A_1Q رو امتداد میدیم تا SP رو به ترتیب در N,M قطع کنند . (امتدادش منظورم بود )
حالا میدونیم که RQMN مستطیل است . حالا اگه ثابت کنیم که NS = MP است بنابر هم نهشتی دو مثلث RNS , PMQ نتیجه میشه که RS = PQ .


حکم :


چهارضلعی
 محاطی است پس داریم :
محاطی است پس داریم :

که همان نتیجه ای بود که باید می گرفتیم پس حکم ثابت شد .
لطفا رفقا سوال بذارن . من سوال خوبی برای این تاپیک ندارم . [MENTION=18785]Dadgarnia[/MENTION] [MENTION=14921]aras2213[/MENTION]
سوال بعد:
فرض كنيد
 دو ارتفاع در مثلث حاده
دو ارتفاع در مثلث حاده
 از نقطه ي
از نقطه ي
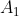 دو عمود بر خطوط
دو عمود بر خطوط
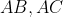 و از نقطه ي
و از نقطه ي
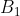 دو عمود بر خطوط
دو عمود بر خطوط
 وارد مي كنيم ثابت كنيد پاي اين چهار عمود تشكيل يك ذوزنقه متساوي الساقين مي دهد.
وارد مي كنيم ثابت كنيد پاي اين چهار عمود تشكيل يك ذوزنقه متساوي الساقين مي دهد.
فرض كنيد
چهارضلعی
چهارضلعی
حالا میایم RB_1 , A_1Q رو امتداد میدیم تا SP رو به ترتیب در N,M قطع کنند . (امتدادش منظورم بود )
حالا میدونیم که RQMN مستطیل است . حالا اگه ثابت کنیم که NS = MP است بنابر هم نهشتی دو مثلث RNS , PMQ نتیجه میشه که RS = PQ .
حکم :
چهارضلعی
که همان نتیجه ای بود که باید می گرفتیم پس حکم ثابت شد .
لطفا رفقا سوال بذارن . من سوال خوبی برای این تاپیک ندارم . [MENTION=18785]Dadgarnia[/MENTION] [MENTION=14921]aras2213[/MENTION]
- ارسال ها
- 159
- لایک ها
- 282
- امتیاز
- 0
پاسخ : ماراتن هندسه version 2
 که در آن
که در آن
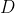 پای ارتفاع نظیر راس
پای ارتفاع نظیر راس
 و
و
 مرکز ارتفاعی مثلث میباشد. حال اگر
مرکز ارتفاعی مثلث میباشد. حال اگر
 آنگاه حکم مساله معادل محاطی بودن
آنگاه حکم مساله معادل محاطی بودن
 است که معادل است با
است که معادل است با
 اما
اما
 پس کافیست بگوییم
پس کافیست بگوییم
 یا
یا
 اما این معادل محاطی بودن
اما این معادل محاطی بودن
 است که معادل است با این که:
است که معادل است با این که:

که رابطه آخر رابطه ای درست است. پس حکم مساله ثابت شد.
سوال بعد:
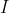 مرکز دایره محاطی مثلث
مرکز دایره محاطی مثلث
 است.
است.
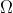 دایره محیطی این مثلث و
دایره محیطی این مثلث و
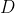 نقطه ای دلخواه روی ضلع
نقطه ای دلخواه روی ضلع
 است. دایره
است. دایره
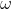 بر
بر
 در
در
 مماس است. ثابت کنید دایره محیطی مثلث
مماس است. ثابت کنید دایره محیطی مثلث
 بر نیمساز این مثلث مماس است.
بر نیمساز این مثلث مماس است.
که رابطه آخر رابطه ای درست است. پس حکم مساله ثابت شد.
سوال بعد:
پاسخ : ماراتن هندسه version 2
 که در آن
که در آن
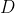 پای ارتفاع نظیر راس
پای ارتفاع نظیر راس
 و
و
 مرکز ارتفاعی مثلث میباشد. حال اگر
مرکز ارتفاعی مثلث میباشد. حال اگر
 آنگاه حکم مساله معادل محاطی بودن
آنگاه حکم مساله معادل محاطی بودن
 است که معادل است با
است که معادل است با
 اما
اما
 پس کافیست بگوییم
پس کافیست بگوییم
 یا
یا
 اما این معادل محاطی بودن
اما این معادل محاطی بودن
 است که معادل است با این که:
است که معادل است با این که:

که رابطه آخر رابطه ای درست است. پس حکم مساله ثابت شد.
سوال بعد:
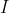 مرکز دایره محاطی مثلث
مرکز دایره محاطی مثلث
 است.
است.
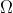 دایره محیطی این مثلث و
دایره محیطی این مثلث و
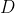 نقطه ای دلخواه روی ضلع
نقطه ای دلخواه روی ضلع
 است. دایره
است. دایره
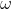 بر
بر
 در
در
 مماس است. ثابت کنید دایره محیطی مثلث
مماس است. ثابت کنید دایره محیطی مثلث
 بر نیمساز این مثلث مماس است.
محل برخورد مماس مشترك دو دايره
بر نیمساز این مثلث مماس است.
محل برخورد مماس مشترك دو دايره
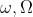 در نقطه
در نقطه
 و
و
 را
را
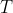 و محل برخورد دوم
و محل برخورد دوم
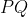 با
با
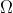 رو
رو
 مي ناميم. داريم:
مي ناميم. داريم:
 محل برخورد
محل برخورد
 با نيمساز راس
با نيمساز راس
 را
را
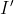 مي ناميم. حالا واضح است كه
مي ناميم. حالا واضح است كه
 پس چهار ضلعي
پس چهار ضلعي
 محاطيه. حالا داريم:
محاطيه. حالا داريم:
 پس دو مثلث
پس دو مثلث
 متشابهن كه نتيجه ميده
متشابهن كه نتيجه ميده
 به راحتي مي تونيم ثابت كنيم
به راحتي مي تونيم ثابت كنيم
 پس
پس
 پس
پس
 و از رابطه
و از رابطه
 حكم نتيجه ميشه.
حكم نتيجه ميشه.
که رابطه آخر رابطه ای درست است. پس حکم مساله ثابت شد.
سوال بعد:













