پاسخ : هندسه
حل قشنگي بود. يه راه ديگه اين سوال اينجوريه كه با همون تعاريف شما،
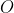 رو نسبت به
رو نسبت به
 قرينه مي كنيم تا به
قرينه مي كنيم تا به
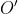 برسيم چون
برسيم چون
 مركز دايره محيطي مثلث
مركز دايره محيطي مثلث
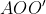 هست و
هست و
 وسط
وسط
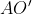 ، نتيجه مي گيريم
، نتيجه مي گيريم
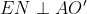 پس حكم ثابت شد.
پس حكم ثابت شد.
سوال جايگزين:
 يك پنج ضلعي محدب است به طوري كه
يك پنج ضلعي محدب است به طوري كه
 . اگر
. اگر
 وسط
وسط
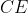 و
و
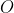 مركز دايره محيطي
مركز دايره محيطي
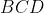 باشد و داشته باشيم
باشد و داشته باشيم
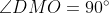 ، ثابت كنيد
، ثابت كنيد
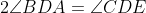 .
.
وسط پاره خط های
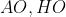 را به ترتیب
را به ترتیب
 می گیریم. واضح است که
می گیریم. واضح است که
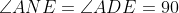 پس
پس
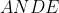 محاطی است.
محاطی است.
الان کافیه ثابت کنیم که
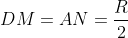 . برای این هم توجه کنید که تجانس به مرکز H و به نسبت 2، نقطه ی D رو به یک نقطه از دایره محیطی و نقطه ی M رو به O تبدیل می کنه. پس
. برای این هم توجه کنید که تجانس به مرکز H و به نسبت 2، نقطه ی D رو به یک نقطه از دایره محیطی و نقطه ی M رو به O تبدیل می کنه. پس
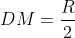 و مساله حل میشه.
و مساله حل میشه.
D:
الان کافیه ثابت کنیم که
D:
سوال جايگزين:
