symmetric point lies on a line
پاسخ : symmetric point lies on a line
فرض کنید میانه متقرن نظیر
 ضلع
ضلع
 را در
را در
 و
و
 را در
را در
 قطع کند داریم
قطع کند داریم
 و
و
 مماسه پس
مماسه پس
 و از طرفی چون
و از طرفی چون
 پس حکم نتیجه میشه
پس حکم نتیجه میشه
فرض کنید میانه متقرن نظیر









پاسخ : symmetric point lies on a line
این که خیلی آسونه مثلا اگه میانه متقارن A دایره محیطی رو تو T قطع کنه
 حالا با تصویر این نقطه ها رو رو خط می ریزیم............
حالا با تصویر این نقطه ها رو رو خط می ریزیم............
همساز قشنگ نیست؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟
:13::13::13::13::13::13::13::13::13::13::13::13::13::13::13::13::13::13::13:
به نظر من قشنگ ترین ابزار هندسه همسازه
حالا میشه اون راه قشنگتون هم بگید:176:
مرسی. هر چند که باید می نوشتید چرا 4 تا نقطه ی p,k,q,a یه گستره ی همساز تشکیل میدند.

(که راه قشنگی هم نیست)
این سوال یه حل خیلی قشنگ داره.
این سوال یه حل خیلی قشنگ داره.
:13::13::13::13::13::13::13::13::13::13::13::13::13::13::13::13::13::13::13:
به نظر من قشنگ ترین ابزار هندسه همسازه
حالا میشه اون راه قشنگتون هم بگید:176:
پاسخ : symmetric point lies on a line
خب این راه حل synthetic تون یه نتیجه از همون همسازست دیگه............
این یه راه کاملا synthetic هستش.
راهنمایی: از L اگه خط های موازی با مثلث PQR (مثلثی که از محل برخورد مماسا به دست میاد) موازی بکشیم تا مثلث رو تو 6 تا نقطه قطع کنه، یه 6 ضلعی محاطی با مرکز L داریم.بقیش راحته.
راهنمایی: از L اگه خط های موازی با مثلث PQR (مثلثی که از محل برخورد مماسا به دست میاد) موازی بکشیم تا مثلث رو تو 6 تا نقطه قطع کنه، یه 6 ضلعی محاطی با مرکز L داریم.بقیش راحته.
پاسخ : symmetric point lies on a line
اون که با هر چی بگی یه راه حل داره
به هر حال من گفتم چون اون همسازه واضحتره هیشکی اول نمیره سراغ اون 6 ضلعی محاطیه وقتی با یه ابزار دیگه (مثلا همساز) حل کرد سعی میکنه سوادی رو که برای حل سوال لازم داره رو کم کنه که این کارا رو میکنه
ضمنن روابط طولی همساز هم خیلی با چهارضلعی محاطی ارتباط داره.............
به هر حال ممنون
بی خیال
اون که با هر چی بگی یه راه حل داره
به هر حال من گفتم چون اون همسازه واضحتره هیشکی اول نمیره سراغ اون 6 ضلعی محاطیه وقتی با یه ابزار دیگه (مثلا همساز) حل کرد سعی میکنه سوادی رو که برای حل سوال لازم داره رو کم کنه که این کارا رو میکنه
ضمنن روابط طولی همساز هم خیلی با چهارضلعی محاطی ارتباط داره.............
به هر حال ممنون
بی خیال
پاسخ : symmetric point lies on a line
فرض کنید که
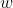 دایره ی محیطی مثلث
دایره ی محیطی مثلث
 باشد. همچنین نقاط
باشد. همچنین نقاط
 به ترتیب مرکز دایره ی محیطی،
به ترتیب مرکز دایره ی محیطی،
محل برخورد دو مماس در نقاط
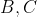 بر دایره ی محیطی و محل برخورد دایره ی محیطی با
بر دایره ی محیطی و محل برخورد دایره ی محیطی با
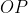 باشد.
باشد.
 از طرفی:
از طرفی:
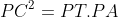
پس:
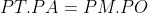 و در نتیجه چهارضلعی
و در نتیجه چهارضلعی
 محاطی است. پس داریم:
محاطی است. پس داریم:
 . اکنون اگر
. اکنون اگر
 آنگاه
آنگاه
 (اینا همش کمانه)
(اینا همش کمانه)
که نتیجه می دهد:
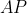 مزدوج هم زاویه ی میانه ی
مزدوج هم زاویه ی میانه ی
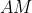 هست. پس
هست. پس
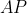 از Lemoine می گذرد.
از Lemoine می گذرد.
حالا اگه از
 موازی اضلاع مثلث مماسی رسم کنیم 6 نقطه ی
موازی اضلاع مثلث مماسی رسم کنیم 6 نقطه ی
 به وجود می آیند. الان واضحه که
به وجود می آیند. الان واضحه که
 بقیشو پس فردا
بقیشو پس فردا
می نویسم
فرض کنید در مثلث
 نقاط
نقاط
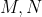 به ترتیب وسط های پاره خط های
به ترتیب وسط های پاره خط های
 باشند که
باشند که
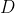 پای ارتفاع راس
پای ارتفاع راس
 می باشد. همچنین فرض نمایید که
می باشد. همچنین فرض نمایید که
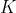 نقطه ی Lemoine باشد.
نقطه ی Lemoine باشد.
ثابت کنید نقاط
 بر یک خط راست قرار گرفته اند.
بر یک خط راست قرار گرفته اند.
ثابت کنید نقاط
محل برخورد دو مماس در نقاط
پس:
که نتیجه می دهد:
حالا اگه از
می نویسم
