پر کردن جدول با اعداد حقیقی
پاسخ : پر کردن جدول با اعداد حقیقی
ببخشین من یه جای سوالو متوجه نشدم : "به طوری که مستطیل
وسط خالی مونده. "
اگه اون مستطیل وسط خالی باشه پس هر خونه ای که توش در نظر بگیریم اطرافیانش خالیه. پس چطوری میتونه عددش میانگین اون خالی ها بشه!؟
ضمنا منظورتون از مرز یعنی فقط محیط مستطیلی که از حذف چهارخونه ی کنارش بوجود اومده!؟
ببخشین من یه جای سوالو متوجه نشدم : "به طوری که مستطیل
اگه اون مستطیل وسط خالی باشه پس هر خونه ای که توش در نظر بگیریم اطرافیانش خالیه. پس چطوری میتونه عددش میانگین اون خالی ها بشه!؟
ضمنا منظورتون از مرز یعنی فقط محیط مستطیلی که از حذف چهارخونه ی کنارش بوجود اومده!؟
پاسخ : پر کردن جدول با اعداد حقیقی
اینطوریه :
خونه‌هایی که x دارن تعیین شدن از قبل ،۴ تا Oها از جدول کنده شدن ، ? هارو باید ما پر کنیم با عدد.
ببخشین من یه جای سوالو متوجه نشدم : "به طوری که مستطیل
\times(n-2))
وسط خالی مونده. "
اگه اون مستطیل وسط خالی باشه پس هر خونه ای که توش در نظر بگیریم اطرافیانش خالیه. پس چطوری میتونه عددش میانگین اون خالی ها بشه!؟
ضمنا منظورتون از مرز یعنی فقط محیط مستطیلی که از حذف چهارخونه ی کنارش بوجود اومده!؟
اگه اون مستطیل وسط خالی باشه پس هر خونه ای که توش در نظر بگیریم اطرافیانش خالیه. پس چطوری میتونه عددش میانگین اون خالی ها بشه!؟
ضمنا منظورتون از مرز یعنی فقط محیط مستطیلی که از حذف چهارخونه ی کنارش بوجود اومده!؟
اینطوریه :
آخرین ویرایش توسط مدیر
پاسخ : پر کردن جدول با اعداد حقیقی
یه ماتریس گنده :10:
(n-2))
در
میسازیم برای معادلاتی که این شرط بهمون تحمیل می‌کنه ، میشه یه ماتریس خلوت اینطوری :
غیر از ۴ تا از سطر‌ها ، که ۲ تا ۲ دارن ، ۲ تا منفی یک .
چون ماتریس ما مربعی هست و میدونیم جواب‌های
یه انتقال از جواب‌های
هستند ، کافی حکم رو فقط در حالتی چک کنیم که خونه هایی که از اول تعیین شدن همگی صفر باشند . یعنی باید در این حالت ثابت کنیم بقیه خونه‌ها هم باید صفر باشند . خوب اینم یه اکسترمال سادست . اگه توی جدولی هر خونه میانگین خونه‌های بغلش باشه ، یا یک سطر یا یک ستون داریم که مقادیر توش فقط شامل ماکسیمم عدد جدول باشه .
یه ماتریس گنده :10:
چون ماتریس ما مربعی هست و میدونیم جواب‌های
پاسخ : پر کردن جدول با اعداد حقیقی
آره..... درسته. یه تعمیم گرافی هم به این صورت داره:
فرض کنید
یه گراف همبند باشه و
زیرمجموعه ای از رئوس
که روی هر راس از
یه عدد حقیقی نوشته شده. میخوایم روی هر راس از رئوس
یه عدد حقیقی بنویسیم به طوری که وقتی همه اعداد رو نوشتیم, هر عدد نوشته شده میانگین اعداد مجاورش باشه. نشون بدین این کار ممکنه.
آره..... درسته. یه تعمیم گرافی هم به این صورت داره:
فرض کنید
پاسخ : پر کردن جدول با اعداد حقیقی
من دو تا راه حل واسه این سوال دارم یکیش با ترکیب های محدب و ....(راه حل معلممون) یه راه حل هم با همگرایی سری ها دارم که مال خودمه!
آره..... درسته. یه تعمیم گرافی هم به این صورت داره:
فرض کنید
یه گراف همبند باشه و
زیرمجموعه ای از رئوس
که روی هر راس از
یه عدد حقیقی نوشته شده. میخوایم روی هر راس از رئوس
یه عدد حقیقی بنویسیم به طوری که وقتی همه اعداد رو نوشتیم, هر عدد نوشته شده میانگین اعداد مجاورش باشه. نشون بدین این کار ممکنه.
فرض کنید
پاسخ : پر کردن جدول با اعداد حقیقی
اينجا هم مي تونه مفيد باشه:AoPS Forum - Graph • Art of Problem Solving
mahanmath:راه حل اصلي كه با همون تركيب محدبه استقرا ميخواد،كه راه سنگينيه!ولي يقينا راه حل hh1456 بايد خيلي جالب باشه!
اينجا هم مي تونه مفيد باشه:AoPS Forum - Graph • Art of Problem Solving
mahanmath:راه حل اصلي كه با همون تركيب محدبه استقرا ميخواد،كه راه سنگينيه!ولي يقينا راه حل hh1456 بايد خيلي جالب باشه!
پاسخ : پر کردن جدول با اعداد حقیقی
برای هر راس مثل v
)
رو بگیرید مجموعه تمام گشت هایی که فقط راس اولشان در S است و به v ختم میشوند
حالا برای هر گشت مثل T که دنباله رئوس آن
است در نظر بگیرید
= n(s)\prod_{i=1}^{n}1/d(v_i))
که در آن
)
عدد راس s است
حالا برای هر راس مثل v از
در نظر بگیرید
=\sum_{T\in A(v)} a(T))
به وضوح این عدد گذاری در شرایط مساله صدق می کند فقط کافی است ثابت کنیم با این تعریف هیچ یک از
)
ها نا متناهی نمی شوند
برای هر راس مثل v
حالا برای هر گشت مثل T که دنباله رئوس آن
حالا برای هر راس مثل v از
آخرین ویرایش توسط مدیر
پاسخ : پر کردن جدول با اعداد حقیقی
سخت ترین تیکه تو این قسمت اینه که نمی دونم چه جوری بنویسم!
(خودمم می فهمم خیلی بد می نویسم) اگه کسی تونست بهتر بنویسه ممنون میشم
فعلن همه این ها رو فرض کنید
رو بگیرید مجموعه همه اعضای
که طول آنها بین i تا i+j هست
و
رو بگیرید همون
با این تفاوت که اون سیگمایی که تو پست قبل نوشتم رو روی همه T هایی در نظر بگیرید که
حالا در نظر بگیرید
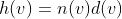و
حالا برای هر
که قبلن تعریف کردم$X^*$ رو بگیرید همون با این تفاوت که گشت هامون محدودیتی برای گذشتن از عضو های S نداردند و
رو بگیرید مجموع تمام
ها در کل گراف
و در نظر بگیرید $X^+=X^*-X$ و
رو بگیرید مجموع تمام
ها در S
حالا ثابت می کنم
برابر
است و
مثبت است که نتیجه میدهد
که نتیجه میدهد اگر
مسیری از v تا یکی از راس های S باشد همواره
که نتیجه می دهد
متناهی است
در ضمن به سادگی می توان نشان داد که این عدد گذاری در صورتی که در هر مولفه همبندی حداقل یک عضو از S آمده باشد یکتاست و همچنین تمامی این اثبات ها قابل تعمیم به حالتی هستند که G گرافی چند گانه است!
سخت ترین تیکه تو این قسمت اینه که نمی دونم چه جوری بنویسم!
(خودمم می فهمم خیلی بد می نویسم) اگه کسی تونست بهتر بنویسه ممنون میشم
فعلن همه این ها رو فرض کنید
و
و در نظر بگیرید $X^+=X^*-X$ و
حالا ثابت می کنم
در ضمن به سادگی می توان نشان داد که این عدد گذاری در صورتی که در هر مولفه همبندی حداقل یک عضو از S آمده باشد یکتاست و همچنین تمامی این اثبات ها قابل تعمیم به حالتی هستند که G گرافی چند گانه است!
آخرین ویرایش توسط مدیر