ماراتن المپیاد ریاضی- کاری از دوره طلا
- شروع کننده موضوع goldeneagle
- تاریخ شروع
- برچسپ ها استفاده اعداد طبیعی المپیاد المپیاد ریاضی المپیادهای علمی ایران ریاضی ریشه سوال طبیعی عدد طبیعی قضیه قوانین ماراتن مربع معادله نظریه اعداد همکاری هندسه پیشرفته یک سوال
- ارسال ها
- 48
- لایک ها
- 173
- امتیاز
- 0
پاسخ : ماراتن المپیاد ریاضی- کاری از دوره طلا
من یک نکته هم به نظرم اومد که بگم.....در یکی از سوالات یک نکته ای ثابت شد و اون هم این بود که :
اگر برای اعداد طبیعی
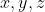 داشته باشیم
داشته باشیم
 انگاه
انگاه
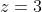 و در این حالت بی نهایت جواب وجود دارد که بررسی شد قبلا .... این نکته را به عنوان یک لم در ذهن داشته باشید. سوالاتی وجود دارند که با vieta jumping حل می شوند و در اصل از این لم استفاده می کنند.... خوب بلد بودن این لم یک گام رو به جلو است!
و در این حالت بی نهایت جواب وجود دارد که بررسی شد قبلا .... این نکته را به عنوان یک لم در ذهن داشته باشید. سوالاتی وجود دارند که با vieta jumping حل می شوند و در اصل از این لم استفاده می کنند.... خوب بلد بودن این لم یک گام رو به جلو است!
من یک نکته هم به نظرم اومد که بگم.....در یکی از سوالات یک نکته ای ثابت شد و اون هم این بود که :
اگر برای اعداد طبیعی
پاسخ : ماراتن المپیاد ریاضی- کاری از دوره طلا
یه چیزی که یک کم مرتبطه فکر کنم:
پست allnames رو ببینید ...
AoPS Forum - A 5 • Art of Problem Solving
یا
AoPS Forum - A 3 • Art of Problem Solving
یه چیزی که یک کم مرتبطه فکر کنم:
پست allnames رو ببینید ...
AoPS Forum - A 5 • Art of Problem Solving
یا
AoPS Forum - A 3 • Art of Problem Solving
- ارسال ها
- 48
- لایک ها
- 173
- امتیاز
- 0
پاسخ : ماراتن المپیاد ریاضی- کاری از دوره طلا
به به شوکی!!!! میبینی من چه خیر و دست به خیر شدم شوکی!!! ماراتن راه میندازم!!! مثل تو همش بیل نمی زنم! :205:
به عارف: کاملا حق با شماست.... به همین دلیل قرار شد در این ماراتن فقط بچه های دوره طلا سوال بذارن تا زمام کار از دستمون در نره و همه ی سوالها یهو گفته نشه! بالاخره در هر یادگیری حل چند سوال هم لازم است ...مثل تمارین پایان یک فصل یک کتاب..اما زیاد از حد نباید باشد...البته سوالی که شما گذاشتید سوال انتخاب تیم 2002 آمریکاست و در برنامه بود....ما بعد از این سوال تنها یک سوال دیگر خواهیم گذاشت و تمام! البته اگر کسی علاقه مند باشد می تواند در پیغام های خصوصی از من یا ماهان یا گودرز یا بهزاد سوال بیشتری بگیرد که من توصیه نمی کنم....
در ضمن خیلی ممنون از بابت تذکرتان....
به به شوکی!!!! میبینی من چه خیر و دست به خیر شدم شوکی!!! ماراتن راه میندازم!!! مثل تو همش بیل نمی زنم! :205:
به عارف: کاملا حق با شماست.... به همین دلیل قرار شد در این ماراتن فقط بچه های دوره طلا سوال بذارن تا زمام کار از دستمون در نره و همه ی سوالها یهو گفته نشه! بالاخره در هر یادگیری حل چند سوال هم لازم است ...مثل تمارین پایان یک فصل یک کتاب..اما زیاد از حد نباید باشد...البته سوالی که شما گذاشتید سوال انتخاب تیم 2002 آمریکاست و در برنامه بود....ما بعد از این سوال تنها یک سوال دیگر خواهیم گذاشت و تمام! البته اگر کسی علاقه مند باشد می تواند در پیغام های خصوصی از من یا ماهان یا گودرز یا بهزاد سوال بیشتری بگیرد که من توصیه نمی کنم....
در ضمن خیلی ممنون از بابت تذکرتان....
پاسخ : ماراتن المپیاد ریاضی- کاری از دوره طلا
فرض کنید نسبت این رابطه ی بخشپذیری tباشه.معادله ی درجه زیر را تشکیل می دهیم. واضحه mوn مخالفند.
که هیچ کدوم جواب نمیده. برای n=1 هم در میاد m=2,3 که هر دو جوابن. که جالبه در هر دو حالت t=5
حالا از روی این دو جواب و اون تبدیلی که ازش جواب کوچکتر ساختیم میشه تمام جواب ها رو ساخت که طبیعتا بی شمار جواب داره.مثلا
فرض کنید نسبت این رابطه ی بخشپذیری tباشه.معادله ی درجه زیر را تشکیل می دهیم. واضحه mوn مخالفند.
m[SUP]2[/SUP]+n[SUP]2[/SUP]-tmn+t=0
فرض کنید m>n و در بین همه ی زوج های mوnکه اون نسبت t بشه اون رو که m مینمم بشه بگیرید. معادله ی بالا جواب دیگری یعنی n[SUP]2[/SUP]+t /m را هم دارد که طبیعیه و برای n>1 با نامساوی نوشتن در می آد m=1,2,3
که هیچ کدوم جواب نمیده. برای n=1 هم در میاد m=2,3 که هر دو جوابن. که جالبه در هر دو حالت t=5
حالا از روی این دو جواب و اون تبدیلی که ازش جواب کوچکتر ساختیم میشه تمام جواب ها رو ساخت که طبیعتا بی شمار جواب داره.مثلا
(1و2) --> (9.2) --> (9و43) --< . . .
برا ی جواب 1و3 هم ممشابها بدست می آد
- ارسال ها
- 327
- لایک ها
- 378
- امتیاز
- 0
پاسخ : ماراتن المپیاد ریاضی- کاری از دوره طلا
@ hkh74
اگر
 آنگاه تنها جواب ممکن
آنگاه تنها جواب ممکن
=(2,2)) است.حال فرض کنید
است.حال فرض کنید
 نباشد:
نباشد:
^2\Rightarrow mn-1|(m-1)^2+(n-1)^2+1)

\Rightarrow (x+y-1)^2=4xy,(x,y)=1 \Rightarrow x=k^2,y=t^2)
^2=1\Rightarrow WLOG:k=t+1\Rightarrow x=(k+1)^2,y=k^2)
^2+1,n=k^2+1)
=((t+1)^2+1,t^2+1)\: \: (t\in \mathbb{N}\cup \left \{ 0 \right \}))
=(t^2+1,(t+1)^2+1)\: \: (t\in \mathbb{N}\cup \left \{ 0 \right \}))
@ hkh74
اگر
حال x را مینیمال فرض کنید و با استفاده از ویت بدست می آید که تنها جواب ممکن
 است. بنابراین:
است. بنابراین:
حال با جایگذاری بدست می آید:
و چون
=P(n,m)) بنابراین خواهیم داشت:
بنابراین خواهیم داشت:
و مجموعه جواب برابر است با این دو خط نهایی اجتماع
) ...
...
آخرین ویرایش توسط مدیر
پاسخ : ماراتن المپیاد ریاضی- کاری از دوره طلا
ولی از معادله ی پل استفاده نشد. اگه جایی اشتباه کردم لطفا بهم بگید.
[HR][/HR]
الان مجموعه ی جواب ها چی شدن؟
توی صورت اصلی سوال گفته شده که فرم صریح جواب ها رو هم پیدا کنید.
mn-1|(n[SUP]2[/SUP]-n+1)[SUP]2[/SUP] -->mn-1|(m+n-1)[SUP]2[/SUP]
حالا این نسبت بخشپذیری رو مثلا t میگیریم. اگر m=n براحتی جواب m=n=2 در میاد. پس فرض می کنیم m>n و در بین تمام زوج های mوn اکه اون نسبت tبشه اونی رو که mمینیمم باشه می گیریم. حالی یه معادله ی درجه 2 بر حسب mداریم.
m[SUP]2[/SUP]+n[SUP]2[/SUP]+1-2mn-2m-2n-tmn+t=0
پس این معادله یه جواب دیگه هم داره که اگه از روی ضرایب و اتحاد ویت حسابش کنیم همون n-1)[SUP]2 [/SUP]+t /m میشه که طبیعیه و با نامساوی میشه نشون داد برای n>1 از m کوچیکتره . که با فرض مینمم بودن m تناقضه. n=1 هم جواب m=2 رو میده.
ولی از معادله ی پل استفاده نشد. اگه جایی اشتباه کردم لطفا بهم بگید.
[HR][/HR]
فرض کنید نسبت این رابطه ی بخشپذیری tباشه.معادله ی درجه زیر را تشکیل می دهیم. واضحه mوn مخالفند.
که هیچ کدوم جواب نمیده. برای n=1 هم در میاد m=2,3 که هر دو جوابن. که جالبه در هر دو حالت t=5
حالا از روی این دو جواب و اون تبدیلی که ازش جواب کوچکتر ساختیم میشه تمام جواب ها رو ساخت که طبیعتا بی شمار جواب داره.مثلا
m[SUP]2[/SUP]+n[SUP]2[/SUP]-tmn+t=0
فرض کنید m>n و در بین همه ی زوج های mوnکه اون نسبت t بشه اون رو که m مینمم بشه بگیرید. معادله ی بالا جواب دیگری یعنی n[SUP]2[/SUP]+t /m را هم دارد که طبیعیه و برای n>1 با نامساوی نوشتن در می آد m=1,2,3
که هیچ کدوم جواب نمیده. برای n=1 هم در میاد m=2,3 که هر دو جوابن. که جالبه در هر دو حالت t=5
حالا از روی این دو جواب و اون تبدیلی که ازش جواب کوچکتر ساختیم میشه تمام جواب ها رو ساخت که طبیعتا بی شمار جواب داره.مثلا
(1و2) --> (9.2) --> (9و43) --< . . .
برای جواب 1و3 هم مشابها بدست می آد
پاسخ : ماراتن المپیاد ریاضی- کاری از دوره طلا
در مورد این سوال هم میشه بطور مشابه از روی جواب ها ی نهایی و اون تبدیل همه ی جواب ها رو ساخت.
فرم صریحش خوب با نوشتن رابطه بازگشتی بدست می آد.
a[SUB]n[/SUB] = -a[SUB]n-2 [/SUB]+ 5a[SUB]n-1[/SUB]
الان مجموعه ی جواب ها چی شدن؟
توی صورت اصلی سوال گفته شده که فرم صریح جواب ها رو هم پیدا کنید.
توی صورت اصلی سوال گفته شده که فرم صریح جواب ها رو هم پیدا کنید.
فرم صریحش خوب با نوشتن رابطه بازگشتی بدست می آد.
a[SUB]n[/SUB] = -a[SUB]n-2 [/SUB]+ 5a[SUB]n-1[/SUB]
آخرین ویرایش توسط مدیر
پاسخ : ماراتن المپیاد ریاضی- کاری از دوره طلا
جوابشو خودم میدونم. گفتم شاید اینم مثل قبلی جوب داشته باشه و جواب هارو به دست نیاورده باشید.
در مورد این سوال هم میشه بطور مشابه از روی جواب ها ی نهایی و اون تبدیل همه ی جواب ها رو ساخت.
فرم صریحش خوب با نوشتن رابطه بازگشتی بدست می آد.
a[SUB]n[/SUB] = -a[SUB]n-2 [/SUB]+ 5a[SUB]n-1[/SUB]
فرم صریحش خوب با نوشتن رابطه بازگشتی بدست می آد.
a[SUB]n[/SUB] = -a[SUB]n-2 [/SUB]+ 5a[SUB]n-1[/SUB]
- ارسال ها
- 327
- لایک ها
- 378
- امتیاز
- 0
پاسخ : ماراتن المپیاد ریاضی- کاری از دوره طلا
ولی از معادله ی پل استفاده نشد. اگه جایی اشتباه کردم لطفا بهم بگید.
[HR][/HR]
اون چیزی که من از این راه حل برداشت کردم اینه که جواب ها متناهی اند. که به وضوح غلطه.
:21:
اون که جواب یه سوال دیگست.
من منظورم اون سوالیه که خودم گذاشته بودم. و همین ash1374 راه حلی نوشت که توضیح نداده چیکار کرده، جواب هارو به دست نیاورده و فقط یه معادله نوشته و گفته فرض کنید یه چیزی مینیمال باشد.
توی حل سوال قبلی که من هیچ جایی ندیدم نوشته باشن
^2+1,t^2+1)) هم جوابه. :lol: پس امکان داره این یکی هم جوب داشته باشه.
هم جوابه. :lol: پس امکان داره این یکی هم جوب داشته باشه.
خب اگه قرار باشه هر سوالی که از vieta jumping میدن یه چیزایی رو کپی کنید که دیگه نمیشه راه حل.
ضمن این که من توی راه حل شما در سوال قبلی هم نفهمیدم چطوری از مینیمال بودن x نتیجه گرفتید که
 .
.
PS: من خودم همیشه جور دیگه ای از این تکنیک استفاده می کنم.
ولی اگه می خواین برای این که ماراتن راه بیفته این سوال رو بچونیم من حرفی ندارم.(هر چند هنوز حل نشده!)
mn-1|(n[SUP]2[/SUP]-n+1)[SUP]2[/SUP] -->mn-1|(m+n-1)[SUP]2[/SUP]
حالا این نسبت بخشپذیری رو مثلا t میگیریم. اگر m=n براحتی جواب m=n=2 در میاد. پس فرض می کنیم m>n و در بین تمام زوج های mوn اکه اون نسبت tبشه اونی رو که mمینیمم باشه می گیریم. حالی یه معادله ی درجه 2 بر حسب mداریم.
m[SUP]2[/SUP]+n[SUP]2[/SUP]+1-2mn-2m-2n-tmn+t=0
پس این معادله یه جواب دیگه هم داره که اگه از روی ضرایب و اتحاد ویت حسابش کنیم همون n-1)[SUP]2 [/SUP]+t /m میشه که طبیعیه و با نامساوی میشه نشون داد برای n>1 از m کوچیکتره . که با فرض مینمم بودن m تناقضه. n=1 هم جواب m=2 رو میده.
ولی از معادله ی پل استفاده نشد. اگه جایی اشتباه کردم لطفا بهم بگید.
[HR][/HR]
(یه دور دیگه post #26 رو بخونین)
اون که جواب یه سوال دیگست.
من منظورم اون سوالیه که خودم گذاشته بودم. و همین ash1374 راه حلی نوشت که توضیح نداده چیکار کرده، جواب هارو به دست نیاورده و فقط یه معادله نوشته و گفته فرض کنید یه چیزی مینیمال باشد.
توی حل سوال قبلی که من هیچ جایی ندیدم نوشته باشن
خب اگه قرار باشه هر سوالی که از vieta jumping میدن یه چیزایی رو کپی کنید که دیگه نمیشه راه حل.
ضمن این که من توی راه حل شما در سوال قبلی هم نفهمیدم چطوری از مینیمال بودن x نتیجه گرفتید که
PS: من خودم همیشه جور دیگه ای از این تکنیک استفاده می کنم.
ولی اگه می خواین برای این که ماراتن راه بیفته این سوال رو بچونیم من حرفی ندارم.(هر چند هنوز حل نشده!)
- ارسال ها
- 48
- لایک ها
- 173
- امتیاز
- 0
پاسخ : ماراتن المپیاد ریاضی- کاری از دوره طلا
ماهان الان خوابه ولی قراره خودش بیاید حلهای شما را برای سوالی که گذاشته بخونه و بررسی کنه.... به محض این که اون سوال بررسی شد میریم سراغ سوال بعد....سوال بعد همون سوال انتخاب تیم 2002 آمریکاست که آقا عارف قبلا گذاشته بودن (دوستان لطفا از این به بعد وظیفه سوال گذاشتن را به ما محول کنید!!!) البته من بازم صورت سوال رو مینویسم اما
تا وقتی ماهان تکلیف این راه حلها رو معلوم نکرده به سراغ اون سوال نروید لطفا! بذارید نظم ماراتن حفظ بشه! خدا خیرتون بده! :4:
در آخر هم واقعا با این استقبالتون ما رو دلگرم کردید! :41:
ماهان الان خوابه ولی قراره خودش بیاید حلهای شما را برای سوالی که گذاشته بخونه و بررسی کنه.... به محض این که اون سوال بررسی شد میریم سراغ سوال بعد....سوال بعد همون سوال انتخاب تیم 2002 آمریکاست که آقا عارف قبلا گذاشته بودن (دوستان لطفا از این به بعد وظیفه سوال گذاشتن را به ما محول کنید!!!) البته من بازم صورت سوال رو مینویسم اما
تا وقتی ماهان تکلیف این راه حلها رو معلوم نکرده به سراغ اون سوال نروید لطفا! بذارید نظم ماراتن حفظ بشه! خدا خیرتون بده! :4:
در آخر هم واقعا با این استقبالتون ما رو دلگرم کردید! :41:
پاسخ : ماراتن المپیاد ریاضی- کاری از دوره طلا
معذرت می خوام آقا عارف. من نفهمیدم شما کدوم سوالو میگین.اون سوالی که صورتش بود mn-1|(n[SUP]2[/SUP]-n+1)[SUP]2 [/SUP]حق با شماست. من اول اشتباه کردم و همه ی جواب ها رو بدست نیاوردم ولی بعد گفتم که از روی رابطه بازگشتی 2a[SUB]n-1 [/SUB]-a[SUB]n-1[/SUB]=a[SUB]n[/SUB] جواب های دیگه بدست می آد . البته به علاوه ی جواب 2 و 2. یعنی هر دو عضو متوالی از اون دنباله که همون n[SUP]2[/SUP]+1 هستن یه جواب مسئله است.
اون سوالی هم که خودتون گذاشتین راه حل من توی پست #25 هستش. اون راهی که بالا گذاشتین مال سوال بالاییه که گفتم اشتباه کرده بودم. بعد گفتین فرم صریحش چیه که گفتم با اون رابطه بازگشتی فرم صریحش بدست می آد. البته دو نوع جواب داشت که رابطه بازگشتیشون یکیه ولی جوله ی دومشون فرق داره.
حالا یکی از بچه ها اگه میشه لطف کنه بگه کدوم سوال راه حلش هنوز کامل نیست تا ما بیشتر روش فک کنیم.
[HR][/HR]
ببخشید در مورد اون سوال بحث کردم پست بالایی رو ندیدم.
معذرت می خوام آقا عارف. من نفهمیدم شما کدوم سوالو میگین.اون سوالی که صورتش بود mn-1|(n[SUP]2[/SUP]-n+1)[SUP]2 [/SUP]حق با شماست. من اول اشتباه کردم و همه ی جواب ها رو بدست نیاوردم ولی بعد گفتم که از روی رابطه بازگشتی 2a[SUB]n-1 [/SUB]-a[SUB]n-1[/SUB]=a[SUB]n[/SUB] جواب های دیگه بدست می آد . البته به علاوه ی جواب 2 و 2. یعنی هر دو عضو متوالی از اون دنباله که همون n[SUP]2[/SUP]+1 هستن یه جواب مسئله است.
اون سوالی هم که خودتون گذاشتین راه حل من توی پست #25 هستش. اون راهی که بالا گذاشتین مال سوال بالاییه که گفتم اشتباه کرده بودم. بعد گفتین فرم صریحش چیه که گفتم با اون رابطه بازگشتی فرم صریحش بدست می آد. البته دو نوع جواب داشت که رابطه بازگشتیشون یکیه ولی جوله ی دومشون فرق داره.
حالا یکی از بچه ها اگه میشه لطف کنه بگه کدوم سوال راه حلش هنوز کامل نیست تا ما بیشتر روش فک کنیم.
[HR][/HR]
ببخشید در مورد اون سوال بحث کردم پست بالایی رو ندیدم.
پاسخ : ماراتن المپیاد ریاضی- کاری از دوره طلا
در مورد این سوال :
AoPS Forum - Find all m,n such that mn-1|m^2+n^2 • Art of Problem Solving
http://www.artofproblemsolving.com/Forum/viewtopic.php?f=56&t=383697&p=2128463&hilit=mn+1+m^2+n^2#p2128463
سوال بعدی:
تمام
 هایی از اعداد طبیعی را بیابید که
هایی از اعداد طبیعی را بیابید که
 .
.
تمام
AoPS Forum - Find all m,n such that mn-1|m^2+n^2 • Art of Problem Solving
http://www.artofproblemsolving.com/Forum/viewtopic.php?f=56&t=383697&p=2128463&hilit=mn+1+m^2+n^2#p2128463
پاسخ : ماراتن المپیاد ریاضی- کاری از دوره طلا
ما گفتیم تا استاد ماهان خوابن به این سوال لینک بدیم (راه حل که نزاشتم):4:
راستی سراغ هندسه و ترکیبیات هم میرین شما ؟ یعنی تکنیک هایی از اونا هم میزارین ؟
در آخر شما هم ما رو به بچه های دوره طلا دلگرم کردین :196::25::4::15:
ماهان الان خوابه ولی قراره خودش بیاید حلهای شما را برای سوالی که گذاشته بخونه و بررسی کنه.... به محض این که اون سوال بررسی شد میریم سراغ سوال بعد....سوال بعد همون سوال انتخاب تیم 2002 آمریکاست که آقا عارف قبلا گذاشته بودن (دوستان لطفا از این به بعد وظیفه سوال گذاشتن را به ما محول کنید!!!) البته من بازم صورت سوال رو مینویسم اما
تا وقتی ماهان تکلیف این راه حلها رو معلوم نکرده به سراغ اون سوال نروید لطفا! بذارید نظم ماراتن حفظ بشه! خدا خیرتون بده! :4:
در آخر هم واقعا با این استقبالتون ما رو دلگرم کردید! :41:
تا وقتی ماهان تکلیف این راه حلها رو معلوم نکرده به سراغ اون سوال نروید لطفا! بذارید نظم ماراتن حفظ بشه! خدا خیرتون بده! :4:
در آخر هم واقعا با این استقبالتون ما رو دلگرم کردید! :41:
راستی سراغ هندسه و ترکیبیات هم میرین شما ؟ یعنی تکنیک هایی از اونا هم میزارین ؟
در آخر شما هم ما رو به بچه های دوره طلا دلگرم کردین :196::25::4::15:
- ارسال ها
- 48
- لایک ها
- 173
- امتیاز
- 0
پاسخ : ماراتن المپیاد ریاضی- کاری از دوره طلا
اولا لطفا سراغ اون سوال نروید یعنی لطفا راجع بهش بحث نکنید :68: ...ماهان هم رفته بیرون عصر میاد که بخونه حلها رو..... میتونید خودتون روی اون سوال فکر کنید اما اینجا روش بحث نکنید...اگه خیلی علاقه مندید آماده کنید به محض این که سوال قبل تموم شد حلش رو بذارید!!!!!!!!!!!!! در ضمن اینجا لینک دادن کراهت داره!!!!! :3:
بله سراغ همه ی درسها میرویم انشاالله!
اولا لطفا سراغ اون سوال نروید یعنی لطفا راجع بهش بحث نکنید :68: ...ماهان هم رفته بیرون عصر میاد که بخونه حلها رو..... میتونید خودتون روی اون سوال فکر کنید اما اینجا روش بحث نکنید...اگه خیلی علاقه مندید آماده کنید به محض این که سوال قبل تموم شد حلش رو بذارید!!!!!!!!!!!!! در ضمن اینجا لینک دادن کراهت داره!!!!! :3:
بله سراغ همه ی درسها میرویم انشاالله!
پاسخ : ماراتن المپیاد ریاضی- کاری از دوره طلا
دوستان سعی کنید حرفای این پست علیرضا یادتون باشه: http://www.irysc.com/forum/t6886-2/#post90587
ما میخوایم این سوالا اینجا بررسی بشن تا بچه ها راه حلشو کامل یاد بگیرن و احیانا اگه اشکالی تو راه خودشون داشتن برطرف بشه. سعی می کنیم همه درسارو پوشش بدیم, ولی این خیلی به همکاری شما هم بستگی داره.
ممنون
دوستان سعی کنید حرفای این پست علیرضا یادتون باشه: http://www.irysc.com/forum/t6886-2/#post90587
ما میخوایم این سوالا اینجا بررسی بشن تا بچه ها راه حلشو کامل یاد بگیرن و احیانا اگه اشکالی تو راه خودشون داشتن برطرف بشه. سعی می کنیم همه درسارو پوشش بدیم, ولی این خیلی به همکاری شما هم بستگی داره.
ممنون
