یک سوال حد از ارشد
پاسخ : یک سوال حد از ارشد
راهتون قشنگ بود.اما تشریحی تر حلش کنیم!!می خوام کاربرد روش های مختلف رو روی این سوال ببینیم!!
سوال رو از یه دید دیگه هم حل کنید!!
نمیشه از x در مقابل exp صرف نظر کرد؟ با توجه به نامساوی رشد ؟
سوال رو از یه دید دیگه هم حل کنید!!
اگه x به سمت منفی بی نهایت بره چی ؟؟؟
اون موقع دیگه نامساوی رشد کمک نمی کنه
اون موقع دیگه نامساوی رشد کمک نمی کنه
آخرین ویرایش توسط مدیر
- ارسال ها
- 2,223
- لایک ها
- 1,216
- امتیاز
- 0
پاسخ : یک سوال حد از ارشد
راه دیگه دارم اقا مهران:
قضیه کوشی: اگر
 و
و
 باشد آنگاه
باشد آنگاه

حالا برای x های طبیعی ثابت میکنم:

که در محاسبه حد آخر از رشد استفاده شده. پس:
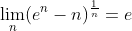
حالا چون برای اعداد طبیعی ثابت کردم کافیه ثابت کنم برای x های بزرگتر از 1 صعودیه . که با مشتق حل میشه ولی چون توی محاسبات ایده هایی به کار رفته,براتون مینویسم:
 حالا مشتق میگیریم:
حالا مشتق میگیریم:

حالا باید ثابت کنیم که حاصل عبارت بالا مثبت است پس:

حالا اگر ثابت کنیم
 است حکم ثابت میشه که بدیهیه(
است حکم ثابت میشه که بدیهیه(
 ) در نتیجه تابع به e میل میکنه.
) در نتیجه تابع به e میل میکنه.
ببخشید طولانی شد !!

راه دیگه دارم اقا مهران:
قضیه کوشی: اگر
حالا برای x های طبیعی ثابت میکنم:
حالا چون برای اعداد طبیعی ثابت کردم کافیه ثابت کنم برای x های بزرگتر از 1 صعودیه . که با مشتق حل میشه ولی چون توی محاسبات ایده هایی به کار رفته,براتون مینویسم:
ببخشید طولانی شد !!
پاسخ : یک سوال حد از ارشد
عالی بود.اما هنوز یه روش دیگه هست.تا فردا فکر کنید.فردا روشم رو میذارم!!
راه دیگه دارم اقا مهران:
قضیه کوشی: اگر
 و
و
 باشد آنگاه
باشد آنگاه

حالا برای x های طبیعی ثابت میکنم:
}{e^{n}-n}=\lim_{n}\frac{e-\frac{n-1}{e^{n}}}{1-\frac{n}{e^{n}}}=e)
که در محاسبه حد آخر از رشد استفاده شده. پس:
^{\frac{1}{n}}=e)
حالا چون برای اعداد طبیعی ثابت کردم کافیه ثابت کنم برای x های بزرگتر از 1 صعودیه . که با مشتق حل میشه ولی چون توی محاسبات ایده هایی به کار رفته,براتون مینویسم:
^{\frac{1}{x}}\Rightarrow&space;lny=ln(e^{x}-x)^{\frac{1}{x}}=\frac{1}{x}ln(e^{x}-x)) حالا مشتق میگیریم:
حالا مشتق میگیریم:
}{x^{2}}\Rightarrow&space;{y}'=y[\frac{1}{x}&space;\cdot&space;\frac{e^{x}-1}{e^{x}-x}-\frac{ln(e^{x}-x)}{x^{2}}])
حالا باید ثابت کنیم که حاصل عبارت بالا مثبت است پس:
}-\frac{ln(e^{x}-x)}{x^{2}}>&space;0\Rightarrow\frac{e^{x}-1}{e^{x}-x}>\frac{ln(e^{x}-x)}{x}&space;\Rightarrow&space;\frac{x(e^{x}-1)}{e^{x}-x}>&space;ln(e^{x}-x)\Rightarrow&space;e^{\frac{x(e^{x}-1)}{e^{x}-x}}>&space;e^{x}-x)
حالا اگر ثابت کنیم
}{e^{x}-x}>x) است حکم ثابت میشه که بدیهیه(
است حکم ثابت میشه که بدیهیه(
 ) در نتیجه تابع به e میل میکنه.
) در نتیجه تابع به e میل میکنه.
ببخشید طولانی شد !!

قضیه کوشی: اگر
حالا برای x های طبیعی ثابت میکنم:
حالا چون برای اعداد طبیعی ثابت کردم کافیه ثابت کنم برای x های بزرگتر از 1 صعودیه . که با مشتق حل میشه ولی چون توی محاسبات ایده هایی به کار رفته,براتون مینویسم:
ببخشید طولانی شد !!
پاسخ : یک سوال حد از ارشد
راه دیگر هم دارم البته قبلش یه قضیه درست کردم و از نظر شهودی درسته ولی اثبات نکردم اگر کسی اثبات کرد یا مثال نقض اورد بگه):
اگر کسی اثبات کرد یا مثال نقض اورد بگه):
قضیه: برای هر تابع که از نقطه ی M به بعد مشتقپذیر باشد و در هیچ نقطه ای مشتق صفر نشه و همچنین برای یک زیر مجموعه نامتناهی از نقاط برد که مولفه های اول این نقاط(دامنه شون)
تا بینهایت ادامه داشته باشه و این زیرمجموعه به L همگرا باشه آنگاه تابع اصلی به L همگرا است( که در کادر توسی این زیرمجوعه که گفتم همان مقادیر تابع به ازای اعداد طبیعی است)
( سعی کنید اول با دید شهودی قضیه براتون جا بیفته بعد اگه شد اثبات یا رد کنید):1:
اثبات راه سوم: در کادر توسی برای زیرمجوعه از برد نامتناهی ثابت کردیم به e همگرایه. و همچنین میدانیم از یک تا بینهایت مشتق پذیره( ترکیب تو مشتقپذیر مشتق پذیره) و راحت میشه نشانداد که مشتق از یک تا بینهایت 0 نمیشه پس طبق قضیه خودم:4: تابع به e همگرایه.
توجه: من برای استفاده از این راه و ساختن قضیه از شکلی که اقا مهران در پستای قبلیش گذاشته بود ایده گرفتم.شما هم برای اینکه قضیه و راهم جا بیفته نگاهه به ص قبل پست mehran88 نگاه بیندازید !!:4::4:
راه دیگه دارم اقا مهران:
قضیه کوشی: اگر
 و
و
 باشد آنگاه
باشد آنگاه

حالا برای x های طبیعی ثابت میکنم:

که در محاسبه حد آخر از رشد استفاده شده. پس:
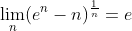
قضیه کوشی: اگر
حالا برای x های طبیعی ثابت میکنم:
قضیه: برای هر تابع که از نقطه ی M به بعد مشتقپذیر باشد و در هیچ نقطه ای مشتق صفر نشه و همچنین برای یک زیر مجموعه نامتناهی از نقاط برد که مولفه های اول این نقاط(دامنه شون)
تا بینهایت ادامه داشته باشه و این زیرمجموعه به L همگرا باشه آنگاه تابع اصلی به L همگرا است( که در کادر توسی این زیرمجوعه که گفتم همان مقادیر تابع به ازای اعداد طبیعی است)
( سعی کنید اول با دید شهودی قضیه براتون جا بیفته بعد اگه شد اثبات یا رد کنید):1:
اثبات راه سوم: در کادر توسی برای زیرمجوعه از برد نامتناهی ثابت کردیم به e همگرایه. و همچنین میدانیم از یک تا بینهایت مشتق پذیره( ترکیب تو مشتقپذیر مشتق پذیره) و راحت میشه نشانداد که مشتق از یک تا بینهایت 0 نمیشه پس طبق قضیه خودم:4: تابع به e همگرایه.
توجه: من برای استفاده از این راه و ساختن قضیه از شکلی که اقا مهران در پستای قبلیش گذاشته بود ایده گرفتم.شما هم برای اینکه قضیه و راهم جا بیفته نگاهه به ص قبل پست mehran88 نگاه بیندازید !!:4::4:
پاسخ : یک سوال حد از ارشد
حالا روشم رو میذارم.
راه سوم جناب torna تقریبا شبیه به اینیه که می خوام بنویسم اما خیلی جمع و جور تر و تر و تمیز تر.
اولین باری که از این روش استفاده کردم توی حد
^x) بود و قبلا جای دیگه ای ندیدم از این روش استفاده بشه. این روشی که می خوام بنویسم کاربرد خیلی گسترده ای توی حد های بی نهایت داره.نه تنها حد هایی که دامنه شون اعداد حقیقیه.بلکه بعضی از حد هایی که دامنه شون اعداد طبیعیه هم میشه از این روش استفاده کرد.مثلا تابع رو به توان x می رسونیم و کار های زیر رو انجام میدیم و در نهایت به جای x یک میذاریم.حالا اینجا دامنه اعداد حقیقیه و کارمون سبکتره.
بود و قبلا جای دیگه ای ندیدم از این روش استفاده بشه. این روشی که می خوام بنویسم کاربرد خیلی گسترده ای توی حد های بی نهایت داره.نه تنها حد هایی که دامنه شون اعداد حقیقیه.بلکه بعضی از حد هایی که دامنه شون اعداد طبیعیه هم میشه از این روش استفاده کرد.مثلا تابع رو به توان x می رسونیم و کار های زیر رو انجام میدیم و در نهایت به جای x یک میذاریم.حالا اینجا دامنه اعداد حقیقیه و کارمون سبکتره.
اول یه قضیه رو بیان می کنم و میرم سراغ حل سوال.
قضیه.اگر تابعی با دامنه اعداد حقیقی و مشتقپذیر در دامنه ش داشته باشیم آنگاه این تابع در بی نهایت تمامی رفتارهای مجانب رو به خودش میگیره که یکی از اونها برابر شدن مشتق تابع و مجانبه که داریم. (اگه مجانب افقی باشه)
=0,and,\lim_{x\rightarrow%20\infty%20}f(x)=L)
اثبات اون قسمت صفر شدن مشتق هم به نظر خودم با برهان خلف میشه انجام داد!
اول با فرض همگرا بودن تابع مورد سوال پیش میریم اگه تابع همگرا نبود آخرای کار یه گیرایی پیش میاد.اگه به مشکلی برنخوریم تابع همگراست و نیازی به اثباتای خفن نداره و از روش میگذریم.
^{\frac{1}{x}}=L)
^{\frac{1}{x}}\times%20\frac{1}{x}(-ln(e^x-x)^{\frac{1}{x}}+\frac{e^x-1}{e^x-x})=0)
=0)

شاید توی این سوال راه خوبی نباشه راه من اما کاربردش خیلی زیاده و جاهایی که خیلی گیر می کنیم اون قضیه ای که نوشتم وحشتناک راهگشاست.همون طور که گفتم میشه روی اعداد طبیعی هم اجراش کرد که از مزیت هاشه!!
حالا روشم رو میذارم.
راه سوم جناب torna تقریبا شبیه به اینیه که می خوام بنویسم اما خیلی جمع و جور تر و تر و تمیز تر.
اولین باری که از این روش استفاده کردم توی حد
اول یه قضیه رو بیان می کنم و میرم سراغ حل سوال.
قضیه.اگر تابعی با دامنه اعداد حقیقی و مشتقپذیر در دامنه ش داشته باشیم آنگاه این تابع در بی نهایت تمامی رفتارهای مجانب رو به خودش میگیره که یکی از اونها برابر شدن مشتق تابع و مجانبه که داریم. (اگه مجانب افقی باشه)
اثبات اون قسمت صفر شدن مشتق هم به نظر خودم با برهان خلف میشه انجام داد!
اول با فرض همگرا بودن تابع مورد سوال پیش میریم اگه تابع همگرا نبود آخرای کار یه گیرایی پیش میاد.اگه به مشکلی برنخوریم تابع همگراست و نیازی به اثباتای خفن نداره و از روش میگذریم.
پس یا L=0 یا پرانتز صفره.اگه L=0 باشه به کمک نا مساوی رشد خیلی راحت ردش می کنیم.
پس داریم
پس داریم
شاید توی این سوال راه خوبی نباشه راه من اما کاربردش خیلی زیاده و جاهایی که خیلی گیر می کنیم اون قضیه ای که نوشتم وحشتناک راهگشاست.همون طور که گفتم میشه روی اعداد طبیعی هم اجراش کرد که از مزیت هاشه!!

