اثبات گنگ بودن عدد
- شروع کننده موضوع Seyed Amir Hosseini
- تاریخ شروع
- برچسپ ها ahzolfaghari dadgarnia j.karimi math sepidfekr اثبات اعداد تعریف حمید آنالیز رادیکال ریشه ریشه صحیح سوال طبیعی عدد اول معادله چند جمله ای کتاب گنگ
پاسخ : اثبات گنگ بودن عدد
می دونم اثباتش از برهان خلفه فعلا دارم روش فک می کنم اگه شد می نویسم
---- دو نوشته به هم متصل شده است ----
اگر فرض کنیم رادیکال دو عددی گویا به شکل
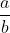 باشه که aوbنسبت به هم اول باشند بایستی داشته باشیم:
باشه که aوbنسبت به هم اول باشند بایستی داشته باشیم:
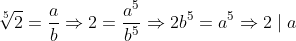
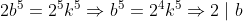
و نتیجه می گیریم که 2 ب.م.م این دو عدد را عاد می کند اما از آنجایی که ب.م.م برابر 1 است در واقع به تناقض می رسیم که یعنی این عدد گنگ است
---- دو نوشته به هم متصل شده است ----
البته به نظرم چون عدد مورد نظر عددی اول بود به همین راحتی میشه اونو اثبات کرد و فکر کنم از این روش بتوان اثبات کرد ریشه nام هر عدد اول عبارتی گنگ است.(n>1)
می دونم اثباتش از برهان خلفه فعلا دارم روش فک می کنم اگه شد می نویسم
---- دو نوشته به هم متصل شده است ----
اگر فرض کنیم رادیکال دو عددی گویا به شکل
و نتیجه می گیریم که 2 ب.م.م این دو عدد را عاد می کند اما از آنجایی که ب.م.م برابر 1 است در واقع به تناقض می رسیم که یعنی این عدد گنگ است
---- دو نوشته به هم متصل شده است ----
البته به نظرم چون عدد مورد نظر عددی اول بود به همین راحتی میشه اونو اثبات کرد و فکر کنم از این روش بتوان اثبات کرد ریشه nام هر عدد اول عبارتی گنگ است.(n>1)
آخرین ویرایش توسط مدیر
پاسخ : اثبات گنگ بودن عدد
به طور کلی
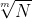 اگه طبیعی نباشه گنگه چون این عدد ریشه ی معادله ی
اگه طبیعی نباشه گنگه چون این عدد ریشه ی معادله ی
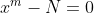 هست و چند جمله ای های تکین اگه ریشه ی گویا داشته باشند همون ریشه صحیح هم هست در حالی که ما شرط گذاشته بودیم که
هست و چند جمله ای های تکین اگه ریشه ی گویا داشته باشند همون ریشه صحیح هم هست در حالی که ما شرط گذاشته بودیم که
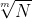 صحیح نیست پس به تناقض می رسیم.
صحیح نیست پس به تناقض می رسیم.
سلام به همگی بچه ها تو کتاب میرزاخوانی یه توضیح کوتاه درمورد اعداد گویا داده بود بعد زیرش نوشته بود اثبات گنگ بودن عدد می تواند بسیار پیچیده باشد اگه ممکنه یه نفر اثبات گنگ بودن رادیکال 2 به فرجه ی پنج را بنویسه
پاسخ : اثبات گنگ بودن عدد
با عرض معذرت پاسخ اصلاح شد
---- دو نوشته به هم متصل شده است ----
ببخشید امیشه بیشتر توضیح بدین چرا اگه
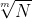 اگه طبیعی نباشه گنگه ؟؟
اگه طبیعی نباشه گنگه ؟؟
چون بنابر توضیحات شما x میتواند عبارتی گویا باشد؟
فک کنم فرجه را اشتباه دیده فرجا پنجه
---- دو نوشته به هم متصل شده است ----
به طور کلی
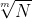 اگه طبیعی نباشه گنگه چون این عدد ریشه ی معادله ی
اگه طبیعی نباشه گنگه چون این عدد ریشه ی معادله ی
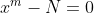 هست و چند جمله ای های تکین اگه ریشه ی گویا داشته باشند همون ریشه صحیح هم هست در حالی که ما شرط گذاشته بودیم که
هست و چند جمله ای های تکین اگه ریشه ی گویا داشته باشند همون ریشه صحیح هم هست در حالی که ما شرط گذاشته بودیم که
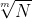 صحیح نیست پس به تناقض می رسیم.
صحیح نیست پس به تناقض می رسیم.
چون بنابر توضیحات شما x میتواند عبارتی گویا باشد؟
پاسخ : اثبات گنگ بودن عدد
قضیه: اگر چند جمله ای
 ریشه ای گویا مانند
ریشه ای گویا مانند
 داشته باشد به طوریکه
داشته باشد به طوریکه
 ، بدست می آید
، بدست می آید
 .
.
اثبات این قضیه خیلی ساده است البته توی کتاب خانم میرزاخانی هم اثباتش هست. چند جمله ای که ما اینجا داریم چند جمله ای
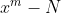 هست حالا اگه
هست حالا اگه
 ریشه ای گویا از این چند جمله ای باشه که
ریشه ای گویا از این چند جمله ای باشه که
 طبق قضیه ی بالا بدست میاد
طبق قضیه ی بالا بدست میاد
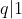 پس
پس
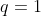 که نتیجه میده این ریشه یه عدد صحیحه اما بدیهتا اگه
که نتیجه میده این ریشه یه عدد صحیحه اما بدیهتا اگه
 توان
توان
 ام کامل نباشه
ام کامل نباشه
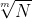 عدد صحیح نیست که طبق چیز هایی که بدست اومد نتیجه میده
عدد صحیح نیست که طبق چیز هایی که بدست اومد نتیجه میده
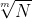 گویا هم نیست و این یعنی این عدد گنگه.
گویا هم نیست و این یعنی این عدد گنگه.
---- دو نوشته به هم متصل شده است ----
مثلا عدد لیوویل که به صورت
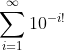 تعریف میشه. البته اثبات گنگ بودن این عدد چندان هم سخت نیست همچنین این عدد متعالی هم هست.
تعریف میشه. البته اثبات گنگ بودن این عدد چندان هم سخت نیست همچنین این عدد متعالی هم هست.
با عرض معذرت پاسخ اصلاح شد
---- دو نوشته به هم متصل شده است ----
ببخشید امیشه بیشتر توضیح بدین چرا اگه
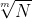 اگه طبیعی نباشه گنگه ؟؟
اگه طبیعی نباشه گنگه ؟؟
چون بنابر توضیحات شما x میتواند عبارتی گویا باشد؟
---- دو نوشته به هم متصل شده است ----
ببخشید امیشه بیشتر توضیح بدین چرا اگه
چون بنابر توضیحات شما x میتواند عبارتی گویا باشد؟
اثبات این قضیه خیلی ساده است البته توی کتاب خانم میرزاخانی هم اثباتش هست. چند جمله ای که ما اینجا داریم چند جمله ای
---- دو نوشته به هم متصل شده است ----
ببخشید پس مثلا منظور از بسیار پیچیده بودن اثبات چه فرمی از اعداد گنگ است؟ چون به نظرم اثبات اعداد گنگ به صورتی که شما بیان کردید خیلی پیچیده نیست آیا فرمی از اعداد گنگ وجود داره که اثباتش پیچیده تر بشه؟
