از مرحله دو تا جهانی
پاسخ : از مرحله دو تا جهانی
نمی دونم دارم جوب میزنم یا نه ولی فک کنم اینم غلطه چون مثلن لاندا رو یک بذارید بعد a رو هم یک بذارید حالا b,c رو برابر بگیرید و خیلی کوچیک جمله اول که میره به سمت یک جمله دوم و سوم هم با هم برابرن و میشن
 که چون a=1 پس میشه b رو اونقدر کوچیک گرفت که این آقاهه از هر چیزی کمتر شه............:3:
که چون a=1 پس میشه b رو اونقدر کوچیک گرفت که این آقاهه از هر چیزی کمتر شه............:3:
با فرض
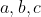 و
و
 اعدادی حقیقی باشند ثابت
اعدادی حقیقی باشند ثابت

(ویرایش شد)
(ویرایش شد)
پاسخ : از مرحله دو تا جهانی
ببخشید دارم در مورد سوال قبل حرف می زنم، چون سوال حل شده من ایده ای که می گفتم رو میذارم (البته متاسفانه من راه دوم ali_irysc رو متوجه نشدم ولی استقرا درسته) :
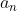 رو به صورت
رو به صورت
 تعریف می کنیم که
تعریف می کنیم که
 . حکم مسئله معادل با اینه که:
. حکم مسئله معادل با اینه که:

از فرض هم نتیجه میگیریم:

که تبدیل میشه به مسئله ی کتاب (104 مسئله ی تئوری اعداد) که با استقرا ثابت میشه.
ببخشید دارم در مورد سوال قبل حرف می زنم، چون سوال حل شده من ایده ای که می گفتم رو میذارم (البته متاسفانه من راه دوم ali_irysc رو متوجه نشدم ولی استقرا درسته) :
از فرض هم نتیجه میگیریم:
که تبدیل میشه به مسئله ی کتاب (104 مسئله ی تئوری اعداد) که با استقرا ثابت میشه.
پاسخ : از مرحله دو تا جهانی
صورت سوال اشتباهه... شکلش رو کشیدم ولی موازی نبود.

در مثلث abcدایره ی محاطی مثلث را میکشیم تا بر bcدرdمماس باشد.adدایره ی مذکور را در kقطع میکند.I1,i2مراکز دایره ی محاطی مثلث های bkd,ckdمیباشد.ثابت کنیدi1i2باbcموازیه.
این سوال فکر کنم مال short listولی نمیدونم چه سالی.در ضمن خودم حل نکردم.
این سوال فکر کنم مال short listولی نمیدونم چه سالی.در ضمن خودم حل نکردم.

پاسخ : از مرحله دو تا جهانی
AoPS Forum - Hard to approach it ! • Art of Problem Solving
فرض کنید T محل برخورد دوم اون دوتا دایره محیطی باشه. ثابت کنید TH نیمساز PTQ هست و نتیجه بگیرین ATH=90. حالا ثابت کنید MH از T رد میشه!!!!!
AoPS Forum - Hard to approach it ! • Art of Problem Solving
فرض کنید T محل برخورد دوم اون دوتا دایره محیطی باشه. ثابت کنید TH نیمساز PTQ هست و نتیجه بگیرین ATH=90. حالا ثابت کنید MH از T رد میشه!!!!!
پاسخ : از مرحله دو تا جهانی
BE ، CF رو ارتفاعهای مثلث بگیرید . دایره AEHF رو هم
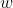 بگیرید
بگیرید
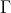 رو هم دایره محیطی بگیرید .
رو هم دایره محیطی بگیرید .
}{P_{w}&space;(Q)}&space;=&space;\frac{\overline{QE}.\overline{QA}}{\overline{PF}.\overline{PA}}&space;=&space;\frac{\overline{QE}}{\overline{PF}}&space;=&space;\frac{\overline{QB}}{\overline{PC}}&space;=&space;\frac{\overline{QB}.\overline{QA}}{\overline{PC}.\overline{PA}}&space;=&space;\frac{P_{\Gamma&space;}&space;(P)}{P_{\Gamma&space;}&space;(Q)})
در مثلث abcازhمرکز ارتفاعی خطی رسم کردیم تاac,abرادرp,qقطع کند کهap=aq.ثابت کنیدhmعمود بر وتر مشترک دو دایره یapq,abcاست(mوسطbc)
پس نسبت قوت P,Q به این ۲ دایره یکیه ، پس طبقه یک لم معروف درباره قوت (در هندسه مسطحه Kurt هم برسی شده) P,Q با محل تقاطع اون ۲ دایرهها هم دایرن . پس کافیه نشون بدیم که HM بر وتر مشترک این ۲ دایره عمود هست که اینم بدیهیه چون H ، M و تقاطع غیر از A
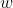 ,
,
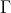 با هم هم خط هستند !
با هم هم خط هستند !
(برای یه اثبات سریع برای این هم خطی ، میتونید بگید که M روی خط BC و روی دایره نه-نقطه هست پس بعد از انعکاس به مرکز H روی تقاطع اونها هست . اما تصویر BC همون دایره
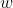 و تصویر نه-نقطه دایره محیطی یعنی
و تصویر نه-نقطه دایره محیطی یعنی
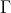 میشه .)
میشه .)
(برای یه اثبات سریع برای این هم خطی ، میتونید بگید که M روی خط BC و روی دایره نه-نقطه هست پس بعد از انعکاس به مرکز H روی تقاطع اونها هست . اما تصویر BC همون دایره


