بررسی سوالات آزمون تشریحی ریاضی 30 بهمن

[M_Sharifi]

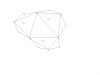
دوستان اگر راه حل و یا نظری در باره ی هریک از سوالات آزمون دارند، می توانند در این تاپیک مطرح کنند:

سوال 1. فرض کنید

دایره ی محیطی مثلث

است.

را وسط کمان

(کمانی که شامل راس

نیست)،

را محل برخورد

و عمودمنصف

،

را محل برخورد

و خط گذرنده از

به موازات

،

را محل برخورد

و

، و

را محل برخورد

و

می نامیم.
ثابت کنید مثلث

متساوی الساقین است.

سوال 2. همه ی اعداد طبیعی

را بیابید که بتوان یک

ضلعی محدب را توسط قطرهایش طوری مثلث بندی کرد که تعداد قطرهایی که از هر راس خارج می شود، زوج باشد. (اگر از راسی قطری خارج نشود، فرض می کنیم تعداد زوجی قطر (صفرتا) از این راس خارج شده است.)

سوال 3. (تألیفی) همه ی اعداد طبیعی

را بیابید که

مکعب کامل شود.

 

[shoki]

dar morede soale 3 ye rahnamayi
moadele ra be in surat benevisid :

aghaye sharifi lotf konid manabee soalat ro ham age mishe zekr konid

 

[bahar23]

براي سوال 2مي شه استقرا زد ؟
بگيم براي هر مضرب سه حكم برقراره .

 

[shoki]

yupyup manham hamin kar ro kardam vali kheyli tulani shod ...

omidvaram rahe halamo bepazirand ....

 

[bahar23]

چرا طولاني ؟
براي 3 و 6 كه بديهيه .
براي حكم استقرا هم 3 تا راس اضافه مي شه . كه البته يكي از اضلاع هم قطر مي شه . 2 تا قطر ديگه مي كشيم و سوال حل مي شه .
البته اگه تونسته باشم منظورمو درست رسونده باشم !!

 

[shoki]

eh...
khob baraye in ke esbat konim ke baraye n=3k mishe in kar ro anjam dad bale rahe hal kutahe vali bayad baraye n=3k+1 va n=3k+2 in ke mitunim in kar ro anjam bedim rad beshe tulani mishe (albate baraye man ...
albate motmaenam rahe hale kutahtari hast ke be dalile zafam dar tarkibiyat behesh naresidam...

 

[seifi_seifi]

برای این که ثابت کنید برای 3k+1 و 3k+2 نمیشه ابتدا بدیهی است که حکم برای n=5,6 اشتباه است و فرض کنید برای n=3,4,5,...,3m

فقط میتوان مضارب 3 را مثلث بندی کرد با شرایط مساله و ثابت میکنیم که برای 3m+1 و 3m+2 نمیتوان این کار را کرد . فرض کنید برای

3m+1 و 3m+2 بتوان مثلث بندی کرد. حال یکی از این مثلث ها انتخاب میکنیم.

این مثلث راس های باقی مانده را به سه قسمت شامل p , q ,r راس تقسیم میکند که هر یک از این دسته ها به همراه دو تا از راس های

مثلث انتخاب شده به طور جداگانه مثلث بندی شده اند و p,q,r از 3m کمتر هستند پس p+2 و q+2 و r+2 طبق فرض بر 3 بخشپذیرند پس

p+q+r+6 نیز بر 3 بخشپذیر است پس p+q+r+3 نیز بر سه بخشپذیر است و چون p+q+r+3 برابر تمام راس ها است پس 3m+1 و 3m+2

نیز بر 3 بخشپذیرند که تناقض است.

دیگه فکر نمیکنم هندسه هم نیاز به توضیح داشته باشه چون خیلی تابلو بود.... .

 

[shoki]

na ye jayi ro faramush kardid momkene ke ...
bezarid namgozari konam farz konid ke ABC un mosalasi bashe ke shoma migin...
unvaght shoma miigin ke chon tuye chand zeliye G_1 bayad hamun etefagh biofte pas bayad tedade azlae G_1 bayad bar 3 bakhshpazir bashe va be hamin tartib baraye G_2 va G_3.
manzuretun hamine?
ama in dorost nist chon ke momkene ke darajeye rouse A va B va C dar har kodum az in chand zeliha fard bashe ...

va injast ke moshkel be vojud miyad ....

 

[seifi_seifi]

اون فرضی رو که تو آخر خط اول کردم نگاه کن.

من نگفتم که p,q,r بر سه بخشپذیر باشند گفتم p+2,q+2,r+2 بر3 بخشپذیر باشد.

بعد با این فرض رفتم جلو که ما توانسته ایم 3m+1 , 3m+2 ضلعی محدب را مثلث بندی کنیم.

اون جوری هم که تو میگی منظورم اینه که تعداد اضلاع G_1 + 1 و G_2 +1 و G_3 +1 بر سه بخشپذیر باشد.

ok?

 

[M_Sharifi]

حل سوال شماره ی 2.
واضح است که حداقل یک ضلع از هر مثلث باید قطری از

ضلعی باشد. یک مثلث را از نوع

می نامیم هرگاه دقیقا

تا از اضلاع آن، قطرهایی از

ضلعی باشند.

را تعداد مثلث های نوع

در نظر می گیریم. در این صورت

[center:4c9ce6989f]

[/center:4c9ce6989f]
در نتیجه

و لذا

. پس مثلثی وجود دارد که دوتا از اضلاع آن، ضلع های

ضلعی اند. فرض کنید این مثلث

باشد. قطر

ضلعی از مثلث دیگری مانند

است. فرض کنید

یا

ضلعی از

ضلعی باشند. اگر مثلا

ضلعی از

ضلعی باشد، آن گاه

. در این صورت هیچ قطر دیگری نمی تواند از

خارج شود، چرا که

را قطع می کند. پس از راس

دقیقا یک قطر خارج شده است، که با شرط مسئله در تناقض است.

بنابراین

و

هر دو، قطرند و لذا مثلث

از نوع

است. پس مجاور با هر مثلث از نوع

، مثلثی از نوع

وجود دارد. اگر مثلث های مجاور با مثلث های از نوع

دو به دو با هم متمایز باشند، آن گاه

، که غیرممکن است. پس دست کم یک دو مثلث از نوع

وجود دارند که با یک مثلث از نوع

مجاورند. بدون از دست دادن کلیت مسئله فرض می کنیم این مثلث های از نوع

،

و

باشند. حالا چندضلعی

را در نظر بگیرید. این چندضلعی توسط قطرهایش مثلث بندی شده است و تعداد قطرهای خارج شده از هر راسش زوج است.

پس اگر

جوابی از مسئله باشد،

نیز جواب مسئله است. بقیه ی راه حل ساده است و در نهایت نتیجه می گیریم که فقط

های به فرم

جواب مسئله اند.

 

[shoki]

bale midunam chi migid man manzuram az chand zeliye G_1 chand zelii hast ke shamele A va B ham mishe ...
shekle zir ro negah konid masalan baraye ye chenin halati estedlale shoma dorost nist ...
manzuram az chand zeliye G_1 chand zeliye ALFKB hast va hamuntor ke mibinid dar kol be surate dorost mosalas bandi shode ama tedade azlae G_1 bar 3 bakhshpazir nist
....
sharmande age bazam manzuretuno motavajeh nashodam ...

 

[shoki]

حالا بذارید من راه حلمو بگم ...
ابتدا همانند آقای شریفی اثبات میشود که مثلثی وجود دارد که دو تا از اضلاع آن بر n ضلعی منطبق باشند ....
حالا استقرا می‌زنیم...
فرض کنید که به ازای n=1,2,...,3k این موضوع اثبات شده باشه .
حالا می‌خواهیم مساله را به ازای n=3k+1,3k+2 اثبات کنیم.
فرض کنید که

مثلثی باشه که دو تا از اضلاع آن بر چند ضلعی منطبق هست.
و از طرفی‌ فرض کنید که

اولین راسی باشه که در جهت
ساعتگرد بعد از

به

وصل باشه .
حالا بدیهیست که

به

وصل است چون اگر نباشد آنگاه مثلث بندی کامل نخواهد بود.
از طرفی‌ هم بدیهیست که

قطر هست چون اگر ضلع باشد آنگاه به راس

فقط یک قطر وصل شده که با فرض مساله در تناقض است ...
نتیجه میگیریم که مثلث

یک مثلثی هست که همهٔ اضلاع آن اقطار میباشند.
حالا این مثلث همانند شکل چند ضلعی را به سه قسمت G_1 و G_2 و G_3 تقسیم می‌کند ...
چون درجه راس

باید زوج باشد و از طرفی‌ در G_2 درجه اش زوج است پس درجه راس

در G_3عددی زوج هست .
و با همین استدلال درجه راس

در G_1 عددی زوج هست .
حال اگر ثابت کنیم که درجه راس

در G_3 و G_1 زوج هست قضیه‌ حله و میتونیم از فرض استقرا استفاده کنیم....
برای این کار هم کافیه فرض خلف ...
پس فرض کنید که درجه تمامی رئوس در G_1 زوج هست ولی‌ درجه راس

در G_1 زوج نیست ...
اما این غیر ممکن چون مجموعه درجات ر,وس در G_1 میشود فرد اما بدیهیست که این مجموع باید زوج باشد زیرا این مجموع برابر با ۲ برابر اقطار رسم شده در G_1 هست .
پس درجه ی راس

زوج می باشد (هم در G_1 و هم در G_3 ) و دیگر کافیست که فرض استقرا را در نظر بگیرید ....

 

[shoki]

راه حلی‌ که دادم همچین طولانی نبود اما برای خود امتحان خیلی‌ طولانی شد ...
همشم به دلیل خنگ بودنم بود ....
الکی‌ اومدم اثبات کردم که اگر دو تا از رئوس مجاور روی چند ضلعی بخاند فرد باشند ولی‌ باقی رئوس زوج در اون صورت‌ 3k+2=n...
که اصلا لزومی نداشت اثبات بشه ....
و کلی از وقتمو گرفت...

حالا از اینا بگذریم ....
بیاین یکمی بیشتر به سوال فکر کنیم ... آیا میشه تعداد طریق های این مثلث بندی رو پیدا کرد...؟

 

[M_Sharifi]

حل سوال 3:

فرض کنید

. اگر

عددی زوج باشد، آن گاه

فرد می شود. اما در این اگر صورت معادله را به پیمانه ی 4 در نظر بگیریم، به رابطه ی نادرست

می رسیم. بنابراین

فرد و درنتیجه

زوج است. باز هم اگر معادله را به پیمانه ی 4 در نظر بگیریم نتیجه می گیریم

.
حالا معادله را به صورت زیر بازنویسی می کنیم:

[center:d51d2cc17e]

[/center:d51d2cc17e]توجه کنید که

[center:d51d2cc17e]

[/center:d51d2cc17e]پس هر یک از عبارت های مثبت

و

عامل اولی به فرم

دارند. فرض کنید

عامل اولی به فرم

از

باشد. در این صورت

[center:d51d2cc17e]

[/center:d51d2cc17e]طبق نتیجه ی معروفی که از قضیه ی فرما حاصل می شود، نتیجه می گیریم

[center:d51d2cc17e]

[/center:d51d2cc17e] با ترکیب این دو رابطه نتیجه می گیریم

. پس

. با همین استدلال،

. اما اگر

آن گاه

[center:d51d2cc17e]

[/center:d51d2cc17e]که غیرممکن است. پس معادله ی داده شده، جوابی در مجموعه ی اعداد طبیعی ندارد.

 

[shoki]

same solution

فقط یه سوال اگه ما میخواستیم از این قضایا که گفتین استفاده کنیم اون وقت باید اثباتشون میکردیم یا لازم نبود ...؟

 

[Goharshady]

فارسی بنویسید!

 

[M_Sharifi]

same solution

فقط یه سوال اگه ما میخواستیم از این قضایا که گفتین استفاده کنیم اون وقت باید اثباتشون میکردیم یا لازم نبود ...؟

قضایا یا قضیه؟

 

[shoki]

khob manzuram hamun ghaziyeye ferma va in ke agar p | a^2+b^2 angah p|a va p|b

 

[M_Sharifi]

فرما که اثبات نمی خواد. ولی من توصیه می کنم این نتیجه گیری (4k+3) رو اثبات هم بکنید.