بررسی مرحله دوم بیست و نهمین المپیاد ریاضی (سوال 4)
- شروع کننده موضوع b_delshad
- تاریخ شروع
- برچسپ ها استفاده اطلاع رسانی اعداد اعداد حقیقی المپیاد المپیاد ریاضی تساوی تعریف حقیقی ریاضی ریشه سوال عدد طبیعی قبول شدگان متغیر مثبت مجموع مربع مرحله دوم نظرخواهی نکته چند جمله ای
پاسخ : بررسی مرحله دوم بیست و نهمین المپیاد ریاضی (سوال 4)
واضح است که
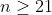 . ثابت می کنیم اگر
. ثابت می کنیم اگر
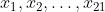 اعدادی در بازه ی [-1,1] با مجموع صفر باشند،
اعدادی در بازه ی [-1,1] با مجموع صفر باشند،
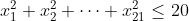
و تساوی زمانی اتفاق می افتد که دقیقا 10 تا از ها برابر منفی 1 و ده تا برابر 1 شوند.
اگر
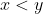 ، برای هر
، برای هر
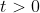 داریم
داریم
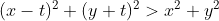 . بنابراین زمانی عبارت
. بنابراین زمانی عبارت
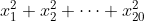 به حداکثر خود می رسد که حداکثر یکی از این متغیر ها یک و یا منفی یک نباشند (در غیر این صورت متغیرهای مخالف 1 و منفی 1 را از هم دور می کنیم تا عبارت افزایش یابد). پس در حالت ماکزیمم، 20 تا از متغیر ها برابر یک یا منفی یک اند و متغیر دیگر بنابراین باید باربر صفر یا یک یا منفی یک باشد (چون جمع متغیرها برابر صفر شده) که فقط یک حالت وجود دارد: 10 تا از متغیرها برابر 1 و ده تا برابر منفی 1 و متغیر دیگر برابر صفر شود (با توجه به فرد بودن 21) که در این صورت مقدار عبارت برابر 20 می شود و تساوی نیز به وضوح فقط در همین حالت اتفاق می افتد.
به حداکثر خود می رسد که حداکثر یکی از این متغیر ها یک و یا منفی یک نباشند (در غیر این صورت متغیرهای مخالف 1 و منفی 1 را از هم دور می کنیم تا عبارت افزایش یابد). پس در حالت ماکزیمم، 20 تا از متغیر ها برابر یک یا منفی یک اند و متغیر دیگر بنابراین باید باربر صفر یا یک یا منفی یک باشد (چون جمع متغیرها برابر صفر شده) که فقط یک حالت وجود دارد: 10 تا از متغیرها برابر 1 و ده تا برابر منفی 1 و متغیر دیگر برابر صفر شود (با توجه به فرد بودن 21) که در این صورت مقدار عبارت برابر 20 می شود و تساوی نیز به وضوح فقط در همین حالت اتفاق می افتد.
بنابراین
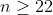 . حالا کافی است یازده تا از متغیرها را برابر
. حالا کافی است یازده تا از متغیرها را برابر
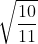 و یازده تای دیگر را برابر
و یازده تای دیگر را برابر
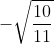 قرار دهیم.
قرار دهیم.
واضح است که
و تساوی زمانی اتفاق می افتد که دقیقا 10 تا از ها برابر منفی 1 و ده تا برابر 1 شوند.
اگر
بنابراین
پاسخ : بررسی مرحله دوم بیست و نهمین المپیاد ریاضی (سوال 4)
من گفتم 20 بعدش فکر کردم گفتم به 1 میل کرده پس میشه 21 بعدشم ثابت کردم که فرد نمیشه. نوشتم 22!
باید در صورت کسر n تا 9 و در مخرج 10 به توان n بذاری. به 1 میل میکنه و 20 تاا عدد میشه. ولی فقط میل میکنه. پس یکی بیشتر میشه.
ولی فرد هم نمیشه چون باید این ور و اون ور 0 مساوی باشن پس زوج میشه و 22 میشه.
من گفتم 20 بعدش فکر کردم گفتم به 1 میل کرده پس میشه 21 بعدشم ثابت کردم که فرد نمیشه. نوشتم 22!
باید در صورت کسر n تا 9 و در مخرج 10 به توان n بذاری. به 1 میل میکنه و 20 تاا عدد میشه. ولی فقط میل میکنه. پس یکی بیشتر میشه.
ولی فرد هم نمیشه چون باید این ور و اون ور 0 مساوی باشن پس زوج میشه و 22 میشه.
