دوستان این حقیر مسائلی را به عنوان تمرین برای استقرا از چند منبع جمع آوری کردم. اگر کسی کمکی می تواند در زمینه برگرداندن این ها به پارسی تک داشته باشد لطفا به من پیغام خصوصی بدهد.
این تمرینات به تدریج اضافه خواهند شد.
قسمت هایی که در پی می آید از جزوه ای از خوزه اسپینوزا به فارسی برگردانده شده اند.
استقرا در نظریه اعداد :
1-فرض کنید
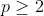 عددی اول و
عددی اول و
 عددی صحیح و نامنفی باشد. همیچنین فرض کنید:
عددی صحیح و نامنفی باشد. همیچنین فرض کنید:

به وسیله استقرا ثابت کنید

2-دنباله فیبوناچی(همانطور که احتمالا می دانید) به این صورت تعریف می شود:
 ,
,
 ,
,

به وسیله استقرای ریاضی ثابت کنید برای تمام
 های صحیح مثبت:
های صحیح مثبت:

3-فرض کنید
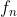 ،
،
 -اُمین عدد دنباله فیبوناچی باشد. حکم زیر را به بیش از یک روش ثابت کنید:
-اُمین عدد دنباله فیبوناچی باشد. حکم زیر را به بیش از یک روش ثابت کنید:

4- فرض کنید
 اعددی اول و فرد باشند به طوریکه
اعددی اول و فرد باشند به طوریکه
 و
و
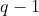 بر
بر
 بخش پذیر نباشد. همین طور فرض کنید
بخش پذیر نباشد. همین طور فرض کنید
 اعدادی صحیح و مثبت باشند به نحویکه به ازای هر عدد صحیح مثبت فرد
اعدادی صحیح و مثبت باشند به نحویکه به ازای هر عدد صحیح مثبت فرد
 داریم:
داریم:
 و همچنین
و همچنین

در ضمن هیچ یک از
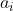 ها نه بر
ها نه بر
 و نه بر
و نه بر
 بخش پذیر نیستند. حال فرض کنید
بخش پذیر نیستند. حال فرض کنید
 و
و
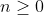
ثابت کنید برای هر عدد صحیح مثبت
 ,
,

5- فرض کنید
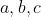 اعدادی صحیح و مثبت باشند بطوریکه
اعدادی صحیح و مثبت باشند بطوریکه
 . فرض کنید
. فرض کنید
 عاملی فرد از
عاملی فرد از
 باشد . برای همه اعداد صحیح و مثبت
باشد . برای همه اعداد صحیح و مثبت
 ثابت کنید :
ثابت کنید :
الف)

ب)

ج) اگر
 بر
بر
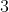 بخش پذیر نباشد آنگاه
بخش پذیر نباشد آنگاه

د)

---- دو نوشته به هم متصل شده است ----
ادامه تمرینات :
6- دنباله
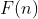 را به اینصورت تعریف می کنیم:
را به اینصورت تعریف می کنیم:
 به ازای هر
به ازای هر
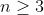 ،
،

ثابت کنید برای هر
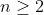
الف)

ب)

7-فرض کنید
 عددی اول به فرم
عددی اول به فرم
 باشد. ثابت کنید به ازای هر
باشد. ثابت کنید به ازای هر
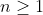

8- ثابت کنید برای همه اعداد صحیح و مثبت
 ،
،
 مربع کامل نیست.
مربع کامل نیست.
9-ثابت کنید به ازای همه اعداد صحیح و مثبت
 ،
،
 مربع کامل نیست.
مربع کامل نیست.
10- ثابت کنید برای هر عدد صحیح و نامنفی
 ،
،

بر
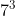 بخش پذیر است.
بخش پذیر است.
ادامه دارد...
---- دو نوشته به هم متصل شده است ----
این تمرینات به تدریج اضافه خواهند شد.
قسمت هایی که در پی می آید از جزوه ای از خوزه اسپینوزا به فارسی برگردانده شده اند.
استقرا در نظریه اعداد :
1-فرض کنید
به وسیله استقرا ثابت کنید
2-دنباله فیبوناچی(همانطور که احتمالا می دانید) به این صورت تعریف می شود:
به وسیله استقرای ریاضی ثابت کنید برای تمام
3-فرض کنید
4- فرض کنید
در ضمن هیچ یک از
ثابت کنید برای هر عدد صحیح مثبت
5- فرض کنید
الف)
ب)
ج) اگر
د)
---- دو نوشته به هم متصل شده است ----
ادامه تمرینات :
6- دنباله
ثابت کنید برای هر
الف)
ب)
7-فرض کنید
8- ثابت کنید برای همه اعداد صحیح و مثبت
9-ثابت کنید به ازای همه اعداد صحیح و مثبت
10- ثابت کنید برای هر عدد صحیح و نامنفی
بر
ادامه دارد...
---- دو نوشته به هم متصل شده است ----
- شما در پیام خود از 77 تصویر استفاده کرده اید. شما مجوز استفاده از 62 تصویر را دارید. لطفا" به صفحه قبل باز گشته و مشکل را برطرف کنید سپس ادامه دهید.
تصاور (منجمله شکلک ها و ... ) از تگ کد vB های و HTML <img> استفاده می کنند. فعال سازی و نحوه استفاده از اینها و تگ های مشابه در اختیار مدیریت کل است.
[/LIST]
[/QUOTE]
این دیگه چه صیغه ایه؟ سه ساعته دارم کار می کنم. چرا همچین می کنید؟ این محدودیت ها لطفی نداره
آخرین ویرایش توسط مدیر
