- ارسال ها
- 119
- لایک ها
- 46
- امتیاز
- 0
سلام دوستان؛متن سوال:
فرض کنید
 عددی طبیعی و
عددی طبیعی و
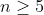 و
و
 کوچکترین عدد اول بزرگتر از
کوچکترین عدد اول بزرگتر از
 باشد.ثابت کنید
باشد.ثابت کنید
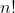 بر اعداد
بر اعداد
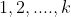 بخشپذیر است.
بخشپذیر است.
اثبات نیمه کامل من:
من فقط راهنمایی می خوام تا اثباتمو تکیمیل کنم.
اگر k کوچکتر از n باشد به وضوح حکم نتیجه می شود پس فرض می کنم k بین n و k+1 باشد و درست اعداد
 بین n و k+1 باشند.در تجزیه
بین n و k+1 باشند.در تجزیه
 به عامل های اول تمامی عامل ها از n کوچکترند چراکه k+1 اولین عدد اول بعد از n است و تمامی اعداد اول کوچتر از این عدد اول از n کوچکترند پس به وضوع !n بر تمامی این اعداد اول بخشپذیر است...
به عامل های اول تمامی عامل ها از n کوچکترند چراکه k+1 اولین عدد اول بعد از n است و تمامی اعداد اول کوچتر از این عدد اول از n کوچکترند پس به وضوع !n بر تمامی این اعداد اول بخشپذیر است...
حالا برای اینکه ثابث کنم نمای این عامل ها در !n بزرگتر-مساوی نمای عامل ها در تجزیه n+j است باید چیکار کنم؟
تو کتاب مریم میرزاخانی هم راهنمایی کرده که می تونید از قضیه چبیشف استفاده کنید.
فرض کنید
اثبات نیمه کامل من:
من فقط راهنمایی می خوام تا اثباتمو تکیمیل کنم.
اگر k کوچکتر از n باشد به وضوح حکم نتیجه می شود پس فرض می کنم k بین n و k+1 باشد و درست اعداد
حالا برای اینکه ثابث کنم نمای این عامل ها در !n بزرگتر-مساوی نمای عامل ها در تجزیه n+j است باید چیکار کنم؟
تو کتاب مریم میرزاخانی هم راهنمایی کرده که می تونید از قضیه چبیشف استفاده کنید.
