سؤال خفن، شاخ و باحال جبر

amir.ekhlasi · 1390/3/17

فرض کنید

$K$

مجموعه ای از اعداد مختلط باشد به طوری که نسبت به جمع و ضرب بسته باشد و

$\mathbb{Q}\subseteq K$

همچنین فرض کنید عدد طبیعی

$n$

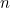وجود داشته باشد به طوری که به ازای هر

$u_1,...,u_n\in K$

، اعداد گویای

$a_1,...,a_n$

وجود داشته باشند به طوری که همه آنها صفر نیستند و

$a_1u_1+...+a_nu_n=0$

. همچنین فرض کنید

$A$

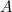مجموعه تمام توابع

$f:K\rightarrow K$

باشد که به ازای هر

$x,y\in K$

،

$f(x+y)=f(x)+f(y)$

و

$f(xy)=f(x)f(y)$

.
الف) ثابت کنید عدد مختلطی مانند

$w\in K$

وجود دارد به طوری که هر

$v\in K$

را میتوان به شکل

$v=b_0+b_1w+b_2w^2+...+b_nw^n$

نوشت که در آن

$b_0,...,b_n\in \mathbb{Q}$

.
ب) فرض کنید

$f\in A$

و

$f\neq 0$

. ثابت کنید

$f$

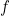یک به یک و پوشا است.
ج) ثابت کنید تعداد اعضای

$A$

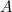متناهی است و مقدار آن کمتر یا مساوی

$n$

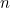است.
د) فرض کنید در الف

$p(x)$

چند جمله ایی با ضرایب گویا باشد که

$w$

ریشه آن است و فرض کنید تمام ریشه های مختلط

$p(x)$

در

$K$

باشند. حال فرض کنید

$u\in K$

. ثابت کنید

$u\in \mathbb{Q}$

اگر و فقط اگر به ازای هر

$f\in A$

،

$f(u)\in \mathbb{Q}$

:188::188:

:189::189::223::223::225::150::150:

khalina · 1390/3/17

پاسخ : سؤال خفن، شاخ و باحال جبر

سلام به شما دوست گرامی،
در انتخاب عنوان برای موضوعات خود به قوانین تالار دقت نمایید.
عنوان شما باید بیانگر خلاصه ای از سوال یا مطلب شما باشد.

موفق و پیروز باشی

amir.ekhlasi · 1390/3/19

پاسخ : سؤال خفن، شاخ و باحال جبر

کسی ایده ای ندارد؟؟

mahanmath · 1390/3/19

پاسخ : سؤال خفن، شاخ و باحال جبر

این مساله یه حالت خاص از یه قضیه معروف هست (البته اون واسه وقتی که K/Q ولی اثباتش اینجا یکیه)

ثابت کن اگه Q(a,b)=K اون موقع یه c وجود داره کهQ(c)= K .

amir.ekhlasi · 1390/3/19

پاسخ : سؤال خفن، شاخ و باحال جبر

فکر کنم قسمت الف حل شد. راه حل طولانیه ولی به این شرح است:
ابتدا میتوان ثابت کرد

$u_1,...,u_n$

وجود دارند که به همراه اعداد گویا تمام

$K$

را میسازند. یعنی مجموعه

$K$

از تمام چند جمله ایها با ضرایب گویا و متغیرهای

$u_1,...,u_n$

ساخته میشود. درواقع

$K=\mathbb{Q}[u_1,...,u_n]$

. نکته دوم اینجاست که اگر

$u\in K$

، آنگاه طبق فرض اعداد گویای

$a_0,...,a_n$

وجود دارند که در آن

$a_0+a_1u+a_2u^2+...+a_nu^n=0$

. درواقع چندجمله ایی با ضرایب گویا وجود دارد که

$u$

ریشه آن است. در ادامه حکم زیر را ثابت میکنیم:
اگر

$v_1,...,v_m\in K$

، آنگاه

$w\in \mathbb{Q}[v_1,...,v_m]$

وجود دارد که در آن

$\mathbb{Q}[w]= \mathbb{Q}[v_1,...,v_m]$

. این حکم مسئله را ثابت میکند.

ادامه در پست بعد ...

amir.ekhlasi · 1390/3/19

پاسخ : سؤال خفن، شاخ و باحال جبر

حکم را به صورت استقراء روی

$m$

ثابت میکنیم. برای

$m=2$

اثبات به شرح زیر است:
فرض کنید

$u,v\in K$

. فرض کنید

$p(x)$

و

$q(x)$

چند جمله ایهایی با ضرایب گویا باشند که به ترتیب

$u$

و

$v$

ریشه آنها هستند. فرض کنید تمام ریشه های

$p(x)$

در

$\mathbb{C}$

عبارت باشند از

$(u=)u_1,...,u_r$

و تمام ریشه های

$q(x)$

در

$\mathbb{C}$

عبارت باشند از

$(v=)v_1,...,v_s$

. عدد گویا

$t$

را چنان انتخاب میکنیم که به ازای هر زوج

$(i,j)\neq (1,1)$

،

$t\neq (u-u_i)/(v-v_j)$

. قرار میدهیم

$w=u+tv$

. نکته اینجاست که به ازای هر زوج مرتب

$(i,j)\neq (1,1)$

،

$w\neq u_i+tv_j$

. ثابت میکنیم

$\mathbb{Q}[w]=\mathbb{Q}[u,v]$

. از آنجا که

$w\in \mathbb{Q}[u,v]$

، پس

$\mathbb{Q}[w]\subseteq \mathbb{Q}[u,v]$

. برای اینکه ثابت کنیم

$\mathbb{Q}[u,v]\subseteq \mathbb{Q}[w]$

، باید ثابت کنیم

$u,v\in \mathbb{Q}[w]$

. قرار میدهیم

$h(x)=p(w-tx)$

. در اینصورت

$h(x)$

یک چند جمله ای با ضرایب

$\mathbb{Q}[w]$

است که

$v$

ریشه آن است. همچنین به ازای هر

$j>1$

،

$v_j$

ریشه آن نیست. درواقع

$q(x)$

و

$h(x)$

تنها یک ریشه مشترک در اعداد مختلط دارند. فرض کنید

$g(x)$

چند جمله ایی با ضرایب

$\mathbb{Q}[w]$

و درجه مینیمم باشد که

$v$

ریشه آن است. از آنجا که درجه این چند جمله ای مینیمم است (طبق قضیه تقسیم) داریم

$g(x)|q(x)$

و

$g(x)|h(x)$

. اما

$q(x)$

و

$h(x)$

تنها یک ریشه مشترک دارند. در نتیجه

$g(x)=(x-v)^k$

. اما اگر

$k>1$

آنگاه

$v$

ریشه

$g'(x)$

است. ولی این خلاف فرض ما در مورد مینیمم بودن درجه است. این به ما می گوید که

$g(x)=x-v$

. در نتیجه

$v\in \mathbb{Q}[w]$

. همچنین

$u=w-tv\in \mathbb{Q}[w]$

. این ثابت میکند

$\mathbb{Q}[u,v]=\mathbb{Q}[w]$

.

ادامه در پست بعد...

amir.ekhlasi · 1390/3/19

پاسخ : سؤال خفن، شاخ و باحال جبر

حال فرض کنید حکم برای

$m=k$

درست باشد. حکم را برای

$m=k+1$

ثابت میکنیم.

$\mathbb{Q}[v_1,...,v_{k+1}]$

را در نظر بگیرید. طبق آنچه ثابت شد میدانیم

$u$

ای وجود دارد که

$\mathbb{Q}[v_1,v_2]=\mathbb{Q}[u]$

. پس

$\mathbb{Q}[v_1,...,v_{k+1}]=\mathbb{Q}[u,v_3,...,v_{k+1}]$

. حال طبق فرض استقراء،

$w$

ای وجود دارد که

$\mathbb{Q}[u,v_3,...,v_{k+1}]=\mathbb{Q}[w]$

. این حکم را ثابت میکند.

این از الف:229::18:

amir.ekhlasi · 1390/3/21

پاسخ : سؤال خفن، شاخ و باحال جبر

ب) ش هم حل شد. راه حل آن آسانتر از الف است:
ابتدا فرض کنید

$u\in K$

و

$u \neq 0$

. فرض کنید

$p(x)$

چند جمله ایی با ضرایب گویا و درجه مینیمم باشد که

$u$

ریشه آن است. چون

$p(x)$

درجه مینیمم را دارد پس

$p(x)$

در

$\mathbb{Q}[x]$

تحویل ناپذیر است. چون

$u \neq 0$

، پس چند جمله ایهای

$p(x)$

و

$x$

نسبت به هم اولند. در نتیجه طبق قضیه بزو، چند جمله ایهای

$q(x),h(x)\in \mathbb{Q}[x]$

وجود دارند که

$p(x)q(x)+xh(x)=1$

. در نتیجه

$uh(u)=1$

. این به ما میگوید که

$u^{-1}=h(u)\in K$

. حال میتوانیم از این موضوع برای اثبات یک به یک بودن تابع

$f \in A$

(

$f \neq 0$

) استفاده کنیم. فرض کنید

$B$

مجموعه تمام صفرهای تابع

$f$

باشد. فرض کنید

$u \in B, u \neq 0$

. در این صورت داریم

$f(1)=f(u)f(u^{-1})=0$

. در نتیجه

$1 \in B$

. این ثابت میکند که

$B=K$

. یعنی

$f=0$

که خلاف فرض ما است. این برهان خلف به ما میگوید که

$B=\left \{ 0 \right \}$

. این ثابت میکند

$f$

یک به یک است. برای پوشا بودن

$f$

میدانیم به ازای هر عدد 'گویایی

$f(a)=a$

. فرض کنید

$u \in K$

و

$p(x)$

چند جمله ایی با ضرایب گویا باشد که

$u$

ریشه آن است. فرض کنید

$C$

مجموعه تمام ریشه های این چند جمله ای در

$K$

. باشد میتوان دید که

$f(C)=C$

. (به این نکته توجه کنید که

$C$

یک مجموعه متناهی است.) در نتیجه

$v \in C$

وجود دارد که

$f(v)=u$

. این ثابت میکند که

$f$

پوشا است.

سؤال خفن، شاخ و باحال جبر

amir.ekhlasi

New Member

khalina

مدیر آیریسک

amir.ekhlasi

New Member

mahanmath

New Member

amir.ekhlasi

New Member

amir.ekhlasi

New Member

amir.ekhlasi

New Member

amir.ekhlasi

New Member