- ارسال ها
- 935
- لایک ها
- 1,654
- امتیاز
- 93
با سلام خدمت همه دوستان.
این تاپیک برای قرار دادن سوالات دوره هستش .......
من سعی می کنم سوالات رو این جا قرار بدم ..... البته به من حق بدید خیلی سریع نتونم این کارو بکنم ..چون هنوز هم امتحانات تموم نشده .....اما سعیم بر اینه که سریع تر بذارم
و از همه رفقا التماس دعا دارم !!
---- دو نوشته به هم متصل شده است ----
سوالات امتحان نظریه اعداد :
1- ثابت کنید بی نهایت عدد طبیعی n وجود دارد بطوریکه نتوان انرا به صورت جمع دو عدد با عوامل اول کمتر از 1394 نوشت .
2-
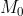 مجموعه ای متناهی از اعداد طبیعی است . علی در هر مرحله عضوی از
مجموعه ای متناهی از اعداد طبیعی است . علی در هر مرحله عضوی از
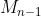 مانند
مانند
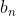 بر می دارد و به وسیله آن
بر می دارد و به وسیله آن
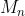 را می سازد.
را می سازد.
ثابت کنید مرحله ای فرامی رسد که برای مجموعه ، هیچ یک از اعضای آن دیگری را عاد نمی کند .
3-
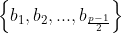 را مجموعه همگی مانده های مربعی به پیمانه p در نظر بگیرید . فرض کنید a,c دو عدد طبیعی اند بطوری که نسبت به p اول اند و p نیز عدد اول فرد است . ثابت کتید حداقل یکی از اعداد مجموعه زیر نیز مانده مربعی است .
را مجموعه همگی مانده های مربعی به پیمانه p در نظر بگیرید . فرض کنید a,c دو عدد طبیعی اند بطوری که نسبت به p اول اند و p نیز عدد اول فرد است . ثابت کتید حداقل یکی از اعداد مجموعه زیر نیز مانده مربعی است .

4-
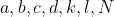 اعداد طبیعی اند . فرض کنید به ازای هر
اعداد طبیعی اند . فرض کنید به ازای هر
 می دانیم عوامل اول دو عدد
می دانیم عوامل اول دو عدد
 و
و
 یکی هستند . ثابت کنید
یکی هستند . ثابت کنید
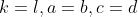
5-
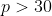 یک عدد اول است . ثابت کنید یکی از اعداد زیر را می توان بصورت جمع دو مربع کامل نوشت .
یک عدد اول است . ثابت کنید یکی از اعداد زیر را می توان بصورت جمع دو مربع کامل نوشت .

این تاپیک برای قرار دادن سوالات دوره هستش .......
من سعی می کنم سوالات رو این جا قرار بدم ..... البته به من حق بدید خیلی سریع نتونم این کارو بکنم ..چون هنوز هم امتحانات تموم نشده .....اما سعیم بر اینه که سریع تر بذارم
و از همه رفقا التماس دعا دارم !!
---- دو نوشته به هم متصل شده است ----
سوالات امتحان نظریه اعداد :
1- ثابت کنید بی نهایت عدد طبیعی n وجود دارد بطوریکه نتوان انرا به صورت جمع دو عدد با عوامل اول کمتر از 1394 نوشت .
2-
ثابت کنید مرحله ای فرامی رسد که برای مجموعه ، هیچ یک از اعضای آن دیگری را عاد نمی کند .
3-
5-
آخرین ویرایش توسط مدیر
