سوال قشنگ هندسه
پاسخ : سوال قشنگ هندسه
نقطه ی تقاطع داره ی ibc را با ab و ac به ترتیب b1 و c1 مینامیم. از فرض نتیجه میشود pc1=pb1 و p روی دایره ی ibc است. O را مرکز دایره ibc مینامیم. Q1 را محل برخورد دوم aq و دایره مینامیم.با یک قوت نتیجه میشه apoq1 محاطی است و با یک تشابه و فرض محاطی بودن apq1 نتیجه میشود ai نیمساز qap است که نتیجه میشود pq || bc1 || cb1 پس pb1=qc و pc1=qb چون pc1=pb1 پس qc=qb پس qq1 نیمساز cqb است.
نقطه ی تقاطع داره ی ibc را با ab و ac به ترتیب b1 و c1 مینامیم. از فرض نتیجه میشود pc1=pb1 و p روی دایره ی ibc است. O را مرکز دایره ibc مینامیم. Q1 را محل برخورد دوم aq و دایره مینامیم.با یک قوت نتیجه میشه apoq1 محاطی است و با یک تشابه و فرض محاطی بودن apq1 نتیجه میشود ai نیمساز qap است که نتیجه میشود pq || bc1 || cb1 پس pb1=qc و pc1=qb چون pc1=pb1 پس qc=qb پس qq1 نیمساز cqb است.
پاسخ : سوال قشنگ هندسه
من که حلتونو متوجه نشدم ولی رابطه
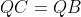 غلطه.
غلطه.
نقطه ی تقاطع داره ی ibc را با ab و ac به ترتیب b1 و c1 مینامیم. از فرض نتیجه میشود pc1=pb1 و p روی دایره ی ibc است. O را مرکز دایره ibc مینامیم. Q1 را محل برخورد دوم aq و دایره مینامیم.با یک قوت نتیجه میشه apoq1 محاطی است و با یک تشابه و فرض محاطی بودن apq1 نتیجه میشود ai نیمساز qap است که نتیجه میشود pq || bc1 || cb1 پس pb1=qc و pc1=qb چون pc1=pb1 پس qc=qb پس qq1 نیمساز cqb است.
پاسخ : سوال قشنگ هندسه
کلیت راه حلتون درسته ولی خیلی سخت حل کردین. راه ساده تر:
فرض می کنیم . وسط کمان
 از دایره محیطی مثلث (کمانی که شامل
از دایره محیطی مثلث (کمانی که شامل
 نیست) رو
نیست) رو
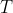 و مرکز دایره محاطی داخلی رو
و مرکز دایره محاطی داخلی رو
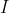 می نامیم. چون
می نامیم. چون
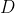 روی محور اصلی دوایر محیطی
روی محور اصلی دوایر محیطی
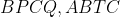 هست نتیجه می گیریم که چهار ضلعی
هست نتیجه می گیریم که چهار ضلعی
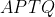 هم محاطی است حالا داریم:
هم محاطی است حالا داریم:
 به طور مشابه داریم
به طور مشابه داریم
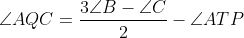 پس کافیه ثابت کنیم
پس کافیه ثابت کنیم
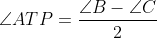 . چون
. چون
 نتیجه می گیریم که
نتیجه می گیریم که
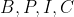 روی دایره ای به مرکز
روی دایره ای به مرکز
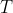 قرار دارند پس
قرار دارند پس
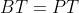 حالا داریم:
حالا داریم:
 پس حکم ثابت شد.
پس حکم ثابت شد.
کلیت راه حلتون درسته ولی خیلی سخت حل کردین. راه ساده تر:
فرض می کنیم . وسط کمان
آخرین ویرایش توسط مدیر
