ماراتن تابع دبیرستانی

حمید آنالیز · 1393/10/24

پاسخ : ماراتن تابع دبیرستانی

ببخشین اون نرم افزاری که دوستمون بالا از برا رسم استفاده کرده چیه؟

_Mobin_ · 1393/10/24

پاسخ : ماراتن تابع دبیرستانی

حمید آنالیز گفت

نرم افزار نیست. سایت wolframalpha.com

mohy1376 · 1393/10/24

پاسخ : ماراتن تابع دبیرستانی

**Mobin** گفت

$f^3(x)+1=g(x)\rightarrow f^3(f^{-1}(x))+1=g(f^{-1}(x))\rightarrow g^{-1}(x^3+1)=f^{-1}(x)=x^3+x+1$

_Mobin_ · 1393/10/25

پاسخ : ماراتن تابع دبیرستانی

سؤال بعد: (ساده)

اگر نقطه A محل تلاقی نمودار تابع

$f(x)=x^3-2x^2+3x-1$

با نمودار وارون آن باشد، فاصلۀ A را از مبدأ مختصات به‌دست آورید.

حمید آنالیز · 1393/10/26

پاسخ : ماراتن تابع دبیرستانی

$f(f^-1(x))=x\rightarrow x=x^3-2x^2+3x-1\rightarrow x^3-2x^2+2x-1=0\Rightarrow (x^2+2)(x-2)=-3\rightarrow x=1\rightarrow f(x)=1\rightarrow R=\sqrt{1+1}=\sqrt{2}$

_Mobin_ · 1393/10/26

پاسخ : ماراتن تابع دبیرستانی

سؤال بعد: ثابت کنید تابع

$\left\{\begin{matrix} f:\mathbb{R}^+\rightarrow \mathbb{R}^+\\ f(x)=x+\sqrt{x} \end{matrix}\right.$

یک‌به‌یک است و ضابطۀ وارون آن را بنویسد.

moham10mad · 1393/10/27

پاسخ : ماراتن تابع دبیرستانی

**Mobin** گفت

با سلام. امید وارم به دردت بخوره.

X[SUB]1[/SUB]+sqrt(X[SUB]1[/SUB]) = X[SUB]2[/SUB]+sqrt(X[SUB]2[/SUB])
(X[SUB]1[/SUB]-X[SUB]2[/SUB]) + (sqrt(X[SUB]1[/SUB]) - sqrt(X[SUB]2[/SUB])) = 0
مزدوج: (sqrt(X[SUB]1[/SUB]) - sqrt(X[SUB]2[/SUB])) * (sqrt(X[SUB]1[/SUB]) + sqrt(X[SUB]2[/SUB])) + (sqrt(X[SUB]1[/SUB]) - sqrt(X[SUB]2[/SUB])) = 0
(sqrt(X[SUB]1[/SUB]) - sqrt(X[SUB]2[/SUB])) * (sqrt(X[SUB]1[/SUB]) + sqrt(X[SUB]2[/SUB]) + 1) = 0
(sqrt(X[SUB]1[/SUB]) + sqrt(X[SUB]2[/SUB]) + 1): همواره مثبت چون R[SUP]+[/SUP]
sqrt(X[SUB]1[/SUB]) - sqrt(X[SUB]2[/SUB]) = 0
sqrt(X[SUB]1[/SUB]) = sqrt(X[SUB]2[/SUB]) => X[SUB]1[/SUB]=X[SUB]2

وارونش هم خودت بنویس دیگه. اگه مشکلی دیگه ای هست بگو
[/SUB]

---- دو نوشته به هم متصل شده است ----

**Mobin** گفت

با سلام. امید وارم به دردت بخوره.

X[SUB]1[/SUB]+sqrt(X[SUB]1[/SUB]) = X[SUB]2[/SUB]+sqrt(X[SUB]2[/SUB])
(X[SUB]1[/SUB]-X[SUB]2[/SUB]) + (sqrt(X[SUB]1[/SUB]) - sqrt(X[SUB]2[/SUB])) = 0
مزدوج: (sqrt(X[SUB]1[/SUB]) - sqrt(X[SUB]2[/SUB])) * (sqrt(X[SUB]1[/SUB]) + sqrt(X[SUB]2[/SUB])) + (sqrt(X[SUB]1[/SUB]) - sqrt(X[SUB]2[/SUB])) = 0
(sqrt(X[SUB]1[/SUB]) - sqrt(X[SUB]2[/SUB])) * (sqrt(X[SUB]1[/SUB]) + sqrt(X[SUB]2[/SUB]) + 1) = 0
(sqrt(X[SUB]1[/SUB]) + sqrt(X[SUB]2[/SUB]) + 1): همواره مثبت چون R[SUP]+[/SUP]
sqrt(X[SUB]1[/SUB]) - sqrt(X[SUB]2[/SUB]) = 0
sqrt(X[SUB]1[/SUB]) = sqrt(X[SUB]2[/SUB]) => X[SUB]1[/SUB]=X[SUB]2

وارونش هم خودت بنویس دیگه. اگه مشکلی دیگه ای هست بگو
[/SUB]

sepidfekr · 1393/10/27

پاسخ : ماراتن تابع دبیرستانی

moham10mad گفت

با سلام. امید وارم به دردت بخوره.

X[SUB]1[/SUB]+sqrt(X[SUB]1[/SUB]) = X[SUB]2[/SUB]+sqrt(X[SUB]2[/SUB])
(X[SUB]1[/SUB]-X[SUB]2[/SUB]) + (sqrt(X[SUB]1[/SUB]) - sqrt(X[SUB]2[/SUB])) = 0
مزدوج: (sqrt(X[SUB]1[/SUB]) - sqrt(X[SUB]2[/SUB])) * (sqrt(X[SUB]1[/SUB]) + sqrt(X[SUB]2[/SUB])) + (sqrt(X[SUB]1[/SUB]) - sqrt(X[SUB]2[/SUB])) = 0
(sqrt(X[SUB]1[/SUB]) - sqrt(X[SUB]2[/SUB])) * (sqrt(X[SUB]1[/SUB]) + sqrt(X[SUB]2[/SUB]) + 1) = 0
(sqrt(X[SUB]1[/SUB]) + sqrt(X[SUB]2[/SUB]) + 1): همواره مثبت چون R[SUP]+[/SUP]
sqrt(X[SUB]1[/SUB]) - sqrt(X[SUB]2[/SUB]) = 0
sqrt(X[SUB]1[/SUB]) = sqrt(X[SUB]2[/SUB]) => X[SUB]1[/SUB]=X[SUB]2

وارونش هم خودت بنویس دیگه. اگه مشکلی دیگه ای هست بگو
[/SUB]

---- دو نوشته به هم متصل شده است ----

با سلام. امید وارم به دردت بخوره.

X[SUB]1[/SUB]+sqrt(X[SUB]1[/SUB]) = X[SUB]2[/SUB]+sqrt(X[SUB]2[/SUB])
(X[SUB]1[/SUB]-X[SUB]2[/SUB]) + (sqrt(X[SUB]1[/SUB]) - sqrt(X[SUB]2[/SUB])) = 0
مزدوج: (sqrt(X[SUB]1[/SUB]) - sqrt(X[SUB]2[/SUB])) * (sqrt(X[SUB]1[/SUB]) + sqrt(X[SUB]2[/SUB])) + (sqrt(X[SUB]1[/SUB]) - sqrt(X[SUB]2[/SUB])) = 0
(sqrt(X[SUB]1[/SUB]) - sqrt(X[SUB]2[/SUB])) * (sqrt(X[SUB]1[/SUB]) + sqrt(X[SUB]2[/SUB]) + 1) = 0
(sqrt(X[SUB]1[/SUB]) + sqrt(X[SUB]2[/SUB]) + 1): همواره مثبت چون R[SUP]+[/SUP]
sqrt(X[SUB]1[/SUB]) - sqrt(X[SUB]2[/SUB]) = 0
sqrt(X[SUB]1[/SUB]) = sqrt(X[SUB]2[/SUB]) => X[SUB]1[/SUB]=X[SUB]2

وارونش هم خودت بنویس دیگه. اگه مشکلی دیگه ای هست بگو
[/SUB]

دستتون درد نکنه!!!
بعد از این همین هایی رو که به انگلیسی تایپ کردید رو توی latex بزنید!!!
توی نوار منو یه علامت

$fx$

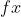هست با اون میتونید کار کنید!!!

mohy1376 · 1393/10/27

پاسخ : ماراتن تابع دبیرستانی

**Mobin** گفت

یه راه دیگه برای نشون دادن یک به یکی:

$f(x)=x+\sqrt{x}\rightarrow f^{'}(x)=1+\frac{1}{2\sqrt{x}}> 0$

صعودیه اکیده و پیوسته پس یک به یکه.

$y=x+\sqrt{x}\rightarrow x+\sqrt{x}-y=0\rightarrow \sqrt{x}=\frac{-1(+?-)\sqrt{1+4y}}{2}\rightarrow f^{-1}(x)=\frac{2+4x-2\sqrt{1+4x}}{4}$

با عدد گذاری می فهمیم که علامت مثبت قابل قبوله.

ماراتن تابع دبیرستانی

حمید آنالیز

Well-Known Member

_Mobin_

New Member

mohy1376

Well-Known Member

_Mobin_

New Member

حمید آنالیز

Well-Known Member

_Mobin_

New Member

moham10mad

New Member

sepidfekr

New Member

mohy1376

Well-Known Member