- ارسال ها
- 1,351
- لایک ها
- 1,322
- امتیاز
- 113
پاسخ : ماراتن جبر (سطح پیشرفته)
خیلی ممنون از حلتون لطفا سوال بعد رو لطف کنین.با تشکر
فکر می کنم به این سوال جواب داده نشده باشد.
ابتدا به این نکته توجه کنید که تابع
 یک به یک و پوشاست. از نکته بعدا در اثبات استفاده می شود.
یک به یک و پوشاست. از نکته بعدا در اثبات استفاده می شود.
داریم:
 از تقارن عبارت و یک به یکی تابع نتیجه می گیریم که برای هر دو عدد حقیقی و مثبت
از تقارن عبارت و یک به یکی تابع نتیجه می گیریم که برای هر دو عدد حقیقی و مثبت
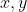 داریم:
داریم:

ادعا می کنیم
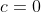 . فرض کنید این طور نباشد. در این صورت دو حالت داریم:
. فرض کنید این طور نباشد. در این صورت دو حالت داریم:
 که در تناقض با پوشایی
که در تناقض با پوشایی
 است.
است.
 که این نیز در تناقض با پوشایی
که این نیز در تناقض با پوشایی
 است.
است.
پس
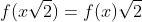 . اکنون از عبارت مساله داریم:
. اکنون از عبارت مساله داریم:

پس


بنابراین:

پوشایی نتیجه می دهد که تابع
 جمعی است.
جمعی است.
از اینجا با توجه به برد تابع
 نتیجه می شود که:
نتیجه می شود که:
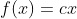
در فرض مساله این تابع را جایگذاری می کنیم و نتیجه می شود که:
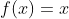
D:
ابتدا به این نکته توجه کنید که تابع
داریم:
ادعا می کنیم
پس
پس
بنابراین:
پوشایی نتیجه می دهد که تابع
از اینجا با توجه به برد تابع
در فرض مساله این تابع را جایگذاری می کنیم و نتیجه می شود که:
D:
