ماراتن جبر (سطح پیشرفته)
پاسخ : ماراتن جبر (سطح پیشرفته)
آهان راست میگی.
https://www.artofproblemsolving.com/community/c6h360818p1974760 فقط عدد هاشون با هم فرق دارن ایده اثبات یکیه.
سوال بعدی رو هم خودت بذار :4:
اینجا اثبات شد که :-؟ چیز دیگه میخوای؟
کلا سوال بعد! :4:
حداکثر تعداد
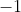 ها در عبارت
ها در عبارت
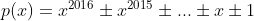 را بیابید تا
را بیابید تا
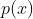 ریشه نداشته باشد.
ریشه نداشته باشد.
کلا سوال بعد! :4:
حداکثر تعداد
https://www.artofproblemsolving.com/community/c6h360818p1974760 فقط عدد هاشون با هم فرق دارن ایده اثبات یکیه.
سوال بعدی رو هم خودت بذار :4:
پاسخ : ماراتن جبر (سطح پیشرفته)
فرض کنید رابطه سوال
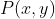 باشه. اگه تابع ثابت باشه بدست میاد
باشه. اگه تابع ثابت باشه بدست میاد
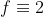 یا
یا
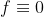 . پس فرض می کنیم تابع ثابت نیست. قرار میدیم
. پس فرض می کنیم تابع ثابت نیست. قرار میدیم
 . داریم:
. داریم:
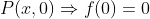


 رابطه ی بالا رو
رابطه ی بالا رو
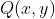 می نامیم. داریم:
می نامیم. داریم:
 بذاریم
بذاریم
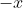 یه تساوی بر حسب
یه تساوی بر حسب
 بدست میاد که چون
بدست میاد که چون
 ثابت نیست می تونیم نتیجه بگیریم که
ثابت نیست می تونیم نتیجه بگیریم که
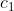 یکی از دو مقدار ۱ و ۳ رو داره و بنابر رابطه (۱)
یکی از دو مقدار ۱ و ۳ رو داره و بنابر رابطه (۱)
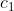 نمی تونه ۳ باشه پس
نمی تونه ۳ باشه پس
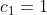 حالا روابط زیر رو داریم:
حالا روابط زیر رو داریم:

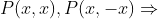


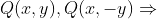


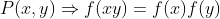 همه ی توابعی که توی دو شرط
همه ی توابعی که توی دو شرط
 و
و
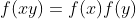 صدق می کنند یه سوال معروفه که فقط جواب های
صدق می کنند یه سوال معروفه که فقط جواب های
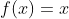 و
و
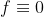 رو داره پس همه ی جواب های سوال بدست اومدن.
رو داره پس همه ی جواب های سوال بدست اومدن.
---- دو نوشته به هم متصل شده است ----
سوال بعد:
اعداد حقیقی
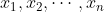 به گونه ای اند که
به گونه ای اند که
 (
(
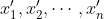 جایگشتی از اعداد
جایگشتی از اعداد
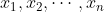 هستند). ثابت کنید
هستند). ثابت کنید
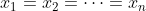 .
.
فرض کنید رابطه سوال
(۱)
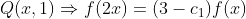
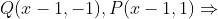

تو رابطه بالا اگه به جای
---- دو نوشته به هم متصل شده است ----
سوال بعد:
اعداد حقیقی
- ارسال ها
- 935
- لایک ها
- 1,654
- امتیاز
- 93
پاسخ : ماراتن جبر (سطح پیشرفته)
سلام به همه بچه های خوب آیریسک . بعد از مدت ها !!


...
حالا همه رو با هم جمع می زنیم و توجه می کنیم
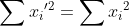
پس

و

و این یعنی :

و این هم معنی حکم مسئله است .
فرض کنید رابطه سوال
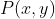 باشه. اگه تابع ثابت باشه بدست میاد
باشه. اگه تابع ثابت باشه بدست میاد
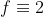 یا
یا
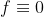 . پس فرض می کنیم تابع ثابت نیست. قرار میدیم
. پس فرض می کنیم تابع ثابت نیست. قرار میدیم
 . داریم:
. داریم:
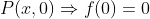


 رابطه ی بالا رو
رابطه ی بالا رو
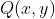 می نامیم. داریم:
می نامیم. داریم:
 بذاریم
بذاریم
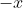 یه تساوی بر حسب
یه تساوی بر حسب
 بدست میاد که چون
بدست میاد که چون
 ثابت نیست می تونیم نتیجه بگیریم که
ثابت نیست می تونیم نتیجه بگیریم که
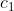 یکی از دو مقدار ۱ و ۳ رو داره و بنابر رابطه (۱)
یکی از دو مقدار ۱ و ۳ رو داره و بنابر رابطه (۱)
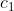 نمی تونه ۳ باشه پس
نمی تونه ۳ باشه پس
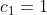 حالا روابط زیر رو داریم:
حالا روابط زیر رو داریم:

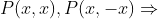


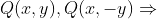


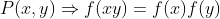 همه ی توابعی که توی دو شرط
همه ی توابعی که توی دو شرط
 و
و
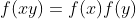 صدق می کنند یه سوال معروفه که فقط جواب های
صدق می کنند یه سوال معروفه که فقط جواب های
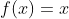 و
و
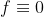 رو داره پس همه ی جواب های سوال بدست اومدن.
رو داره پس همه ی جواب های سوال بدست اومدن.
---- دو نوشته به هم متصل شده است ----
سوال بعد:
اعداد حقیقی
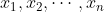 به گونه ای اند که
به گونه ای اند که
 (
(
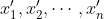 جایگشتی از اعداد
جایگشتی از اعداد
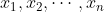 هستند). ثابت کنید
هستند). ثابت کنید
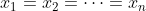 .
.
(۱)
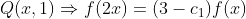
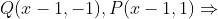

تو رابطه بالا اگه به جای
---- دو نوشته به هم متصل شده است ----
سوال بعد:
اعداد حقیقی
سلام به همه بچه های خوب آیریسک . بعد از مدت ها !!
...
حالا همه رو با هم جمع می زنیم و توجه می کنیم
پس
و
و این یعنی :
و این هم معنی حکم مسئله است .
پاسخ : ماراتن جبر (سطح پیشرفته)

حالا توجه کنید که اگر
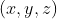 یک جواب از مساله باشد،
یک جواب از مساله باشد،
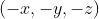 یک جواب مساله خواهد بود. پس بدون کاستن از کلیت مساله می توان فرض کرد که حداقل دو تا از
یک جواب مساله خواهد بود. پس بدون کاستن از کلیت مساله می توان فرض کرد که حداقل دو تا از
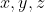 نامنفی هستند. اگر هر سه نامنفی باشند، تناقضی آشکار است. فرض کنید که مثلا
نامنفی هستند. اگر هر سه نامنفی باشند، تناقضی آشکار است. فرض کنید که مثلا
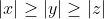 . در این صورت داریم که
. در این صورت داریم که
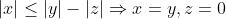 که با نابرابری
که با نابرابری
 در تناقض است.
در تناقض است.
پس یکی از
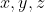 منفی است. فرض کنید که داریم:
منفی است. فرض کنید که داریم:
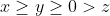
اکنون:

بنابراین

و
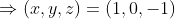
and any permutation is also a solution.
خرکاری بود. P:
سوال بعد:
همه ی سه تایی های حقیقی
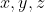 را بیابید که
را بیابید که

همه ی سه تایی های حقیقی
حالا توجه کنید که اگر
پس یکی از
اکنون:
بنابراین
و
and any permutation is also a solution.
خرکاری بود. P:
پاسخ : ماراتن جبر (سطح پیشرفته)
فرض کنید عبارت سوال
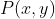 باشه. یه عدد دلخواه و مثبت مثل
باشه. یه عدد دلخواه و مثبت مثل
 رو در نظر می گیریم. واضحه که اگه ثابت کنیم
رو در نظر می گیریم. واضحه که اگه ثابت کنیم
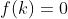 اون وقت برای هر
اون وقت برای هر
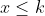 داریم
داریم
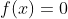 . حالا با فرض
. حالا با فرض
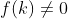 داریم:
داریم:
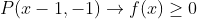

 همینجوری و با استقرا می تونیم ثابت کنیم
همینجوری و با استقرا می تونیم ثابت کنیم
 حالا اگه توی این رابطه قرار بدیم
حالا اگه توی این رابطه قرار بدیم
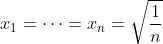 بدست میاد:
بدست میاد:
 حالا چون
حالا چون
 (lim (sqrt(1/n)+1)^n - Wolfram|Alpha :4
(lim (sqrt(1/n)+1)^n - Wolfram|Alpha :4 اگه
اگه
 رو یه عدد ثابت و مثبت در نظر بگیریم وقتی
رو یه عدد ثابت و مثبت در نظر بگیریم وقتی
 رو زیاد کنیم سمت راست از سمت چپ بیشتر میشه که تناقضه پس
رو زیاد کنیم سمت راست از سمت چپ بیشتر میشه که تناقضه پس
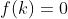 که این هم نتیجه میده
که این هم نتیجه میده
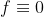 .
.
---- دو نوشته به هم متصل شده است ----
سوال بعد:
فرض کنید
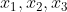 اعدادی حقیقی باشند به طوریکه اعداد
اعدادی حقیقی باشند به طوریکه اعداد
 و
و
 و
و
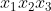 گویا باشند و
گویا باشند و
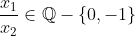 . ثابت کنید
. ثابت کنید
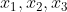 اعدادی گویا هستند.
اعدادی گویا هستند.
فرض کنید عبارت سوال
---- دو نوشته به هم متصل شده است ----
سوال بعد:
فرض کنید
پاسخ : ماراتن جبر (سطح پیشرفته)
تعریف می کنیم:

بنابراین
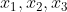 ریشه های چندجمله ای
ریشه های چندجمله ای
 هستند. این چندجمله ای یک چندجمله ای با ضرایب گویاست، پس
هستند. این چندجمله ای یک چندجمله ای با ضرایب گویاست، پس
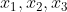 اعداد جبری هستند.
اعداد جبری هستند.
از طرفی می دونیم که:
 که در اینجا
که در اینجا
 عددی گویا و مخالف 1-و0 است.
عددی گویا و مخالف 1-و0 است.
حالا فرض کنید که
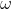 عددی گویا باشد. در این صورت:
عددی گویا باشد. در این صورت:
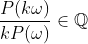
یعنی:

این نتیجه میده که
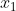 ریشه ی یک چند جمله ای درجه ی دوم با ضرایب گویاست. به همین ترتیب میشه ثابت کرد که
ریشه ی یک چند جمله ای درجه ی دوم با ضرایب گویاست. به همین ترتیب میشه ثابت کرد که
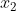 ریشه ی یک چندجمله ای درجه ی دوم با ضرایب گویاست.
ریشه ی یک چندجمله ای درجه ی دوم با ضرایب گویاست.
حالا فرض کنید که
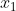 گویا نباشد. (اگر گویا باشد که مساله حل شده است.) در این صورت چون
گویا نباشد. (اگر گویا باشد که مساله حل شده است.) در این صورت چون
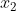 مضرب گویایی از
مضرب گویایی از
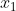 هستش، پس
هستش، پس
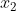 هم گویا نیست. بنابراین،
هم گویا نیست. بنابراین،
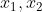 باید مزدوج جبری هم باشند، و این نتیجه می دهد که
باید مزدوج جبری هم باشند، و این نتیجه می دهد که
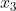 گویاست. حالا داریم:
گویاست. حالا داریم:

که تناقض است. پس هر سه باید گویا باشند.
سوال بعد:
فرض کنید
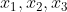 اعدادی حقیقی باشند به طوریکه اعداد
اعدادی حقیقی باشند به طوریکه اعداد
 و
و
 و
و
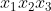 گویا باشند و
گویا باشند و
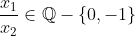 . ثابت کنید
. ثابت کنید
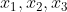 اعدادی گویا هستند.
اعدادی گویا هستند.
فرض کنید
بنابراین
از طرفی می دونیم که:
حالا فرض کنید که
یعنی:
این نتیجه میده که
حالا فرض کنید که
که تناقض است. پس هر سه باید گویا باشند.
پاسخ : ماراتن جبر (سطح پیشرفته)
درسته البته اون تهشو میشد با چند جمله ای مینیمال هم گفت که اگه
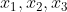 گویا نباشن
گویا نباشن
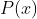 چند جمله ای مینیمالشونه و بقیه اش راحت در میاد.
چند جمله ای مینیمالشونه و بقیه اش راحت در میاد.
سوال بعد:
 عددی حقیقی است و
عددی حقیقی است و
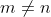 اعدادی طبیعی هستند که
اعدادی طبیعی هستند که
 اعدادی گویا هستند. ثابت کنید
اعدادی گویا هستند. ثابت کنید
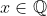 .
.
تعریف می کنیم:

بنابراین
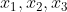 ریشه های چندجمله ای
ریشه های چندجمله ای
 هستند. این چندجمله ای یک چندجمله ای با ضرایب گویاست، پس
هستند. این چندجمله ای یک چندجمله ای با ضرایب گویاست، پس
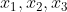 اعداد جبری هستند.
اعداد جبری هستند.
از طرفی می دونیم که:
 که در اینجا
که در اینجا
 عددی گویا و مخالف 1-و0 است.
عددی گویا و مخالف 1-و0 است.
حالا فرض کنید که
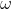 عددی گویا باشد. در این صورت:
عددی گویا باشد. در این صورت:
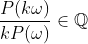
یعنی:

این نتیجه میده که
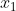 ریشه ی یک چند جمله ای درجه ی دوم با ضرایب گویاست. به همین ترتیب میشه ثابت کرد که
ریشه ی یک چند جمله ای درجه ی دوم با ضرایب گویاست. به همین ترتیب میشه ثابت کرد که
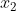 ریشه ی یک چندجمله ای درجه ی دوم با ضرایب گویاست.
ریشه ی یک چندجمله ای درجه ی دوم با ضرایب گویاست.
حالا فرض کنید که
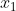 گویا نباشد. (اگر گویا باشد که مساله حل شده است.) در این صورت چون
گویا نباشد. (اگر گویا باشد که مساله حل شده است.) در این صورت چون
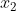 مضرب گویایی از
مضرب گویایی از
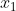 هستش، پس
هستش، پس
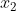 هم گویا نیست. بنابراین،
هم گویا نیست. بنابراین،
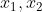 باید مزدوج جبری هم باشند، و این نتیجه می دهد که
باید مزدوج جبری هم باشند، و این نتیجه می دهد که
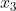 گویاست. حالا داریم:
گویاست. حالا داریم:

که تناقض است. پس هر سه باید گویا باشند.
بنابراین
از طرفی می دونیم که:
حالا فرض کنید که
یعنی:
این نتیجه میده که
حالا فرض کنید که
که تناقض است. پس هر سه باید گویا باشند.
سوال بعد:
