- ارسال ها
- 159
- لایک ها
- 282
- امتیاز
- 0
پاسخ : ماراتن نظریه ی اعداد (سطح ممتاز)
دنباله
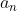 رو از عقب هم ادامه بدید و برای n های منفی هم تعریف کنید.
رو از عقب هم ادامه بدید و برای n های منفی هم تعریف کنید.
بدیهتا
 ، و دقت کنید که
، و دقت کنید که
 یعنی با داشتن سه عضو متوالی دنباله قبلی هم بطور یکتا مشخص میگردد.
یعنی با داشتن سه عضو متوالی دنباله قبلی هم بطور یکتا مشخص میگردد.
حال گرافی m^3 راسی بسازید و هر راسش را با سه تایی مرتبی که هر کدام از اندیس هایش عددی طبیعی بین 1 تا m است برجسب گذاری کنید. از راس با برچسب
 شروع کنید و هر مرحله یالی جهت دار از
شروع کنید و هر مرحله یالی جهت دار از
 به
به
 (ai ها را به پیمانه m در نظر بگیرید)رسم کنید. بدیهتا چون تعداد رئوس گراف متناهی است پس جایی به راس تکراری برخورد میکنیم. اولین جا را در نظر بگیرید که چنین اتفاقی بیفتد. دقت کنید که از آنجا که میتوان از سه عضو متوالی دنباله قبلی را هم پیدا کرد پس درجه ورودی هر راس حداکثر یک است. اما چون هر راس تکراری از راس قبلی اش در دنباله هم یال میگرفته پس اگر اولین راس تکراری همان (0و1و1) نباشد پس یال دیگری هم به آن وارد میشده، که تناقض است. بنابرین دوباره به راس (0و1و1) میرسیم و با ادامه باز هم به این راس میرسیم پس نامتناهی بار به این راس میرسیم، اما رسیدن به این راس همانا و پیدا کردن عددی جدید بخش پذیر بر m همانا، چرا که وجود 0 در این راس نشانگر بخش پذیر بودن عضو اول سه تایی مرتب بر m است که چون عضوی از دنباله است که در رئوس دیگر ظاهر نشده پس عدد جدیدی بخش پذیر بر m داریم پس بینهایت مضرب m در این دنباله موجود است.
(ai ها را به پیمانه m در نظر بگیرید)رسم کنید. بدیهتا چون تعداد رئوس گراف متناهی است پس جایی به راس تکراری برخورد میکنیم. اولین جا را در نظر بگیرید که چنین اتفاقی بیفتد. دقت کنید که از آنجا که میتوان از سه عضو متوالی دنباله قبلی را هم پیدا کرد پس درجه ورودی هر راس حداکثر یک است. اما چون هر راس تکراری از راس قبلی اش در دنباله هم یال میگرفته پس اگر اولین راس تکراری همان (0و1و1) نباشد پس یال دیگری هم به آن وارد میشده، که تناقض است. بنابرین دوباره به راس (0و1و1) میرسیم و با ادامه باز هم به این راس میرسیم پس نامتناهی بار به این راس میرسیم، اما رسیدن به این راس همانا و پیدا کردن عددی جدید بخش پذیر بر m همانا، چرا که وجود 0 در این راس نشانگر بخش پذیر بودن عضو اول سه تایی مرتب بر m است که چون عضوی از دنباله است که در رئوس دیگر ظاهر نشده پس عدد جدیدی بخش پذیر بر m داریم پس بینهایت مضرب m در این دنباله موجود است.
سوال بعد: جدول شطرنجی n*n داریم که اعداد 1 تا
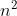 به ترتیبی درون آن قرار داده شده اند. فرض کنید s1 جمع اعداد درون خانه های سیاه و s2 جمع اعداد درون خانه های سفید باشد. همه n هایی را بیابید که به ازای آنها ترتیبی از اعداد 1 تا
به ترتیبی درون آن قرار داده شده اند. فرض کنید s1 جمع اعداد درون خانه های سیاه و s2 جمع اعداد درون خانه های سفید باشد. همه n هایی را بیابید که به ازای آنها ترتیبی از اعداد 1 تا
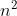 موجود باشد که به ازای آن ترتیب
موجود باشد که به ازای آن ترتیب

دنباله
بدیهتا
حال گرافی m^3 راسی بسازید و هر راسش را با سه تایی مرتبی که هر کدام از اندیس هایش عددی طبیعی بین 1 تا m است برجسب گذاری کنید. از راس با برچسب
سوال بعد: جدول شطرنجی n*n داریم که اعداد 1 تا
