ماراتن نظریه ی اعداد (سطح ممتاز)
پاسخ : ماراتن نظریه ی اعداد (سطح ممتاز)
بله.پس كلا از پايه مشكل داشت! اگه ميشه جواب رو نزاريد يكم بيشتر فكر كنيم
اگه ميشه جواب رو نزاريد يكم بيشتر فكر كنيم
ممنون
---- دو نوشته به هم متصل شده است ----
ببخشيد من يكم گير دادم شما مطمئنيد اين لم غلطه؟
من الان يه سرى كار انجام دادم كه اگر درست باشند(!) لااقل براى حالتى كه p(x) تكين باشد و ضرايب صحيح درسته البته يادمه يه جا ديدمش الان مينويسم
لم شما کلا غلطه.
لم درست برای هر عدد عدد طبیعی مربع باشه ...
لم درست برای هر عدد عدد طبیعی مربع باشه ...
ممنون
---- دو نوشته به هم متصل شده است ----
ببخشيد من يكم گير دادم شما مطمئنيد اين لم غلطه؟
من الان يه سرى كار انجام دادم كه اگر درست باشند(!) لااقل براى حالتى كه p(x) تكين باشد و ضرايب صحيح درسته البته يادمه يه جا ديدمش الان مينويسم
پاسخ : ماراتن نظریه ی اعداد (سطح ممتاز)
لم شما غلطه !!! مثال نقض برای شما :

صورت درست لم : اگر یک چند جمله ای تکین درجه زوج به ازای بی نهایت مقدار مربع کامل باشد انگاه مربع یک چند جمله ای با ضرایب صحیح است !
این لم سوال بلغارستان بوده و اگر این لم رو اثبات کنید متوجه میشید که اثبات اون با اثبات این مساله تفاوت چندانی نمیکنه !!!
راهنمایی : سعی کنید این چند جمله ای رو بین مربع دو چند جمله ای با ضرایب صحیح بندازید !
بله.الان درستش ميكنم
چرا وجود داره http://www.renyi.hu/~p_erdos/1975-46.pdf كه تعميم اين مساله هستش(طبق گفته ى اون كسى كه اين رو گذاشته!)
البته من هم يه كليتى از راه حل ml رو نگاه كردم و فكر كردم حلم درسته.يعنى گفتم بقيش آسونه و ....:65:!ولى الان ميبينم كه يه اشتباه كوچولو(!) كردم و بايد يكم بيشتر فكر كنم ولى فكر ميكنم اون چيزى كه توى pdf هه هستش كامله البته يه رو خونى كردمو فقط حكم مساله رو توش ديدم و متوجه شدم كه درباره ى اون داره صحبت ميكنه!
بيشتر روش فكر ميكنم و اگه حل شد جواب رو مينويسم
ممنون
چرا وجود داره http://www.renyi.hu/~p_erdos/1975-46.pdf كه تعميم اين مساله هستش(طبق گفته ى اون كسى كه اين رو گذاشته!)
البته من هم يه كليتى از راه حل ml رو نگاه كردم و فكر كردم حلم درسته.يعنى گفتم بقيش آسونه و ....:65:!ولى الان ميبينم كه يه اشتباه كوچولو(!) كردم و بايد يكم بيشتر فكر كنم ولى فكر ميكنم اون چيزى كه توى pdf هه هستش كامله البته يه رو خونى كردمو فقط حكم مساله رو توش ديدم و متوجه شدم كه درباره ى اون داره صحبت ميكنه!
بيشتر روش فكر ميكنم و اگه حل شد جواب رو مينويسم
ممنون
صورت درست لم : اگر یک چند جمله ای تکین درجه زوج به ازای بی نهایت مقدار مربع کامل باشد انگاه مربع یک چند جمله ای با ضرایب صحیح است !
این لم سوال بلغارستان بوده و اگر این لم رو اثبات کنید متوجه میشید که اثبات اون با اثبات این مساله تفاوت چندانی نمیکنه !!!
راهنمایی : سعی کنید این چند جمله ای رو بین مربع دو چند جمله ای با ضرایب صحیح بندازید !
پاسخ : ماراتن نظریه ی اعداد (سطح ممتاز)
دستتون درد نکنه.فکر میکنم اثبات لم این جوری باشه(اگه خدا بخواد دیگه احتمالا این درسته)
با مقایسه ضرایب میشه به این نتیجه رسید که چند جمله ای (r(x با ضرایب گویا وجود داره به طورد که درجه اش از n کمتره و

(این قسمت بالا رو خیلی شک دارم)
پس برای x های بزرگ:
 پس
پس
 در نتیجه متناهی تا x طبیعی وجود داره(هنوز مطمنم این سوال رو یه جا دیدم ولی بلغارستان نبوده!)
در نتیجه متناهی تا x طبیعی وجود داره(هنوز مطمنم این سوال رو یه جا دیدم ولی بلغارستان نبوده!)
پس
 و چون p تکین با ضرایب صحیح است طبق لم گاوس q هم با ضریب صحیح است
و چون p تکین با ضرایب صحیح است طبق لم گاوس q هم با ضریب صحیح است
درسته؟
(یادم رفت که بگم درجه p ، برابر 2n هه
لم شما غلطه !!! مثال نقض برای شما :

صورت درست لم : اگر یک چند جمله ای تکین درجه زوج به ازای بی نهایت مقدار مربع کامل باشد انگاه مربع یک چند جمله ای با ضرایب صحیح است !
این لم سوال بلغارستان بوده و اگر این لم رو اثبات کنید متوجه میشید که اثبات اون با اثبات این مساله تفاوت چندانی نمیکنه !!!
راهنمایی : سعی کنید این چند جمله ای رو بین مربع دو چند جمله ای با ضرایب صحیح بندازید !
صورت درست لم : اگر یک چند جمله ای تکین درجه زوج به ازای بی نهایت مقدار مربع کامل باشد انگاه مربع یک چند جمله ای با ضرایب صحیح است !
این لم سوال بلغارستان بوده و اگر این لم رو اثبات کنید متوجه میشید که اثبات اون با اثبات این مساله تفاوت چندانی نمیکنه !!!
راهنمایی : سعی کنید این چند جمله ای رو بین مربع دو چند جمله ای با ضرایب صحیح بندازید !
با مقایسه ضرایب میشه به این نتیجه رسید که چند جمله ای (r(x با ضرایب گویا وجود داره به طورد که درجه اش از n کمتره و
(این قسمت بالا رو خیلی شک دارم)
پس برای x های بزرگ:
پس
درسته؟
(یادم رفت که بگم درجه p ، برابر 2n هه
آخرین ویرایش توسط مدیر
پاسخ : ماراتن نظریه ی اعداد (سطح ممتاز)
فک کنم این لم فقط n زوج رو حل میکنه
لم شما غلطه !!! مثال نقض برای شما :

صورت درست لم : اگر یک چند جمله ای تکین درجه زوج به ازای بی نهایت مقدار مربع کامل باشد انگاه مربع یک چند جمله ای با ضرایب صحیح است !
این لم سوال بلغارستان بوده و اگر این لم رو اثبات کنید متوجه میشید که اثبات اون با اثبات این مساله تفاوت چندانی نمیکنه !!!
راهنمایی : سعی کنید این چند جمله ای رو بین مربع دو چند جمله ای با ضرایب صحیح بندازید !
صورت درست لم : اگر یک چند جمله ای تکین درجه زوج به ازای بی نهایت مقدار مربع کامل باشد انگاه مربع یک چند جمله ای با ضرایب صحیح است !
این لم سوال بلغارستان بوده و اگر این لم رو اثبات کنید متوجه میشید که اثبات اون با اثبات این مساله تفاوت چندانی نمیکنه !!!
راهنمایی : سعی کنید این چند جمله ای رو بین مربع دو چند جمله ای با ضرایب صحیح بندازید !
پاسخ : ماراتن نظریه ی اعداد (سطح ممتاز)
کاملا(مثلا
 ).اما برای بقیه حل کافی است توجه کنیم که وجود دارد
).اما برای بقیه حل کافی است توجه کنیم که وجود دارد
 که
که
 .پس
.پس
 مربع کامل است و این ممکن نیست.
مربع کامل است و این ممکن نیست.
سوال جدید:ثابت کنید برای هر عدد طبیعی a این معادله حداقل یک جواب در مجموع اعداد طبیعی دارد.

دستتون درد نکنه.فکر میکنم اثبات لم این جوری باشه(اگه خدا بخواد دیگه احتمالا این درسته)
با مقایسه ضرایب میشه به این نتیجه رسید که چند جمله ای (r(x با ضرایب گویا وجود داره به طورد که درجه اش از n کمتره و

(این قسمت بالا رو خیلی شک دارم)
پس برای x های بزرگ:
 پس
پس
 در نتیجه متناهی تا x طبیعی وجود داره(هنوز مطمنم این سوال رو یه جا دیدم ولی بلغارستان نبوده!)
در نتیجه متناهی تا x طبیعی وجود داره(هنوز مطمنم این سوال رو یه جا دیدم ولی بلغارستان نبوده!)
پس
 و چون p تکین با ضرایب صحیح است طبق لم گاوس q هم با ضریب صحیح است
و چون p تکین با ضرایب صحیح است طبق لم گاوس q هم با ضریب صحیح است
درسته؟
با مقایسه ضرایب میشه به این نتیجه رسید که چند جمله ای (r(x با ضرایب گویا وجود داره به طورد که درجه اش از n کمتره و
(این قسمت بالا رو خیلی شک دارم)
پس برای x های بزرگ:
پس
درسته؟
سوال جدید:ثابت کنید برای هر عدد طبیعی a این معادله حداقل یک جواب در مجموع اعداد طبیعی دارد.
آخرین ویرایش توسط مدیر
پاسخ : ماراتن نظریه ی اعداد (سطح ممتاز)
http://www.artofproblemsolving.com/Forum/viewtopic.php?f=57&t=589891
کاملا(مثلا
 ).اما برای بقیه حل کافی است توجه کنیم که وجود دارد
).اما برای بقیه حل کافی است توجه کنیم که وجود دارد
 که
که
 .پس
.پس
 مربع کامل است و این ممکن نیست.
مربع کامل است و این ممکن نیست.
سوال جدید:ثابت کنید برای هر عدد طبیعی a این معادله حداقل یک جواب در مجموع اعداد طبیعی دارد.

سوال جدید:ثابت کنید برای هر عدد طبیعی a این معادله حداقل یک جواب در مجموع اعداد طبیعی دارد.
آخرین ویرایش توسط مدیر
پاسخ : ماراتن نظریه ی اعداد (سطح ممتاز)
حدس : بین n عدد طبیعی متوالی یکیش هست که نسبت به هر کدوم دیگه که بگیری، اوله. کسی تا حالا این به گوشش خورده؟ یا کسی میتونه اثبات یا ردش کنه؟
نسبتاً روشنه که از این حدس حکم در میاد...
در مورد این مسئله البته جناب اردوش ثابت کردن که متناهی که هیچی، اصلا جواب نداره. ظاهراً ورژن توان nامش رو هم زحمت کشیدن ثابت کردن ایشون...
ابن مقاله ی حالت مربع کاملشه:
http://www.renyi.hu/~p_erdos/1939-03.pdf
اثبات خیلی اردوشیه! من تا وسطش بیشتر نتونستم دنبال کنم.
حدس : بین n عدد طبیعی متوالی یکیش هست که نسبت به هر کدوم دیگه که بگیری، اوله. کسی تا حالا این به گوشش خورده؟ یا کسی میتونه اثبات یا ردش کنه؟
نسبتاً روشنه که از این حدس حکم در میاد...
در مورد این مسئله البته جناب اردوش ثابت کردن که متناهی که هیچی، اصلا جواب نداره. ظاهراً ورژن توان nامش رو هم زحمت کشیدن ثابت کردن ایشون...
ابن مقاله ی حالت مربع کاملشه:
http://www.renyi.hu/~p_erdos/1939-03.pdf
اثبات خیلی اردوشیه! من تا وسطش بیشتر نتونستم دنبال کنم.
پاسخ : ماراتن نظریه ی اعداد (سطح ممتاز)
اگر اشتباه نکنم در باره این مساله در کتاب اثبات هم صحبت شده !!! کلا این مساله که حاصل ضرب 4 عدد متوالی یا عدد یا 5 عدد در همین سایت هم بررسی شده بود !!!
کلا امسال سوالات انتخاب تیم مثل هر سال نبود !!! ( این مورد در باره مرحله 2 هم صدق میکنه به نظر من مثلا سوال یکش فقط یه تغییر کوچیک توی یه سوال المپیاد کامپیوتر دادن !!! یا ...)
حدس : بین n عدد طبیعی متوالی یکیش هست که نسبت به هر کدوم دیگه که بگیری، اوله. کسی تا حالا این به گوشش خورده؟ یا کسی میتونه اثبات یا ردش کنه؟
نسبتاً روشنه که از این حدس حکم در میاد...
در مورد این مسئله البته جناب اردوش ثابت کردن که متناهی که هیچی، اصلا جواب نداره. ظاهراً ورژن توان nامش رو هم زحمت کشیدن ثابت کردن ایشون...
ابن مقاله ی حالت مربع کاملشه:
http://www.renyi.hu/~p_erdos/1939-03.pdf
اثبات خیلی اردوشیه! من تا وسطش بیشتر نتونستم دنبال کنم.
نسبتاً روشنه که از این حدس حکم در میاد...
در مورد این مسئله البته جناب اردوش ثابت کردن که متناهی که هیچی، اصلا جواب نداره. ظاهراً ورژن توان nامش رو هم زحمت کشیدن ثابت کردن ایشون...
ابن مقاله ی حالت مربع کاملشه:
http://www.renyi.hu/~p_erdos/1939-03.pdf
اثبات خیلی اردوشیه! من تا وسطش بیشتر نتونستم دنبال کنم.
کلا امسال سوالات انتخاب تیم مثل هر سال نبود !!! ( این مورد در باره مرحله 2 هم صدق میکنه به نظر من مثلا سوال یکش فقط یه تغییر کوچیک توی یه سوال المپیاد کامپیوتر دادن !!! یا ...)
پاسخ : ماراتن نظریه ی اعداد (سطح ممتاز)
AoPS Forum - x^y+1=z^2 and a number of different prime divisors • Art of Problem Solving
:4:
AoPS Forum - x^y+1=z^2 and a number of different prime divisors • Art of Problem Solving
:4:
آخرین ویرایش توسط مدیر
پاسخ : ماراتن نظریه ی اعداد (سطح ممتاز)
حالتی که b-a فرد باشد

حالتی که b-a زوج باشد(لطفا نخندید!)
با فرض b>a اون عبارت مساله رو به صورت یه معادله درجه دو مینویسیم بر حسب x. بعد اگر دلتاش رو حساب کنیم و آن را
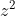 بنامیم و قرار دهیم:
بنامیم و قرار دهیم:
 .حکم مساله با این معادل میشود که عدد t را بیابید به طوری که این عدد ها طبیعی بشن:
.حکم مساله با این معادل میشود که عدد t را بیابید به طوری که این عدد ها طبیعی بشن:

برای این که x طبیعی باشه لازم است که مثبت باشه پس اون عبارت بالا رو بر حسب t به شکل یه معادله درجه دو مینویسیم!اگر دلتاش رو حساب کنیم میبینیم که t توی بازه ای که طولش از 2c بیشتره تغییر میکنه.فکر میکنم که از این بشه نتیجه گرفت که توی این بازه t صحیحی وجود داره که t به پیمانه 2c بشه a.پس x طبیعی و y صحیح میشه.حالا فکر میکنم اگر یکم بیشتر تلاش کنم بتونم کاری کنم که y هم طبیعی شه!:4:
حالا با این حرف ها،این راه حل(حداقل کلیتش) درسته؟!
سوال بعد : a,b اعداد طبیعی هستند. ثابت کنید x,y در اعداد طبیعی وجود دارند که

حالتی که b-a زوج باشد(لطفا نخندید!)
با فرض b>a اون عبارت مساله رو به صورت یه معادله درجه دو مینویسیم بر حسب x. بعد اگر دلتاش رو حساب کنیم و آن را
برای این که x طبیعی باشه لازم است که مثبت باشه پس اون عبارت بالا رو بر حسب t به شکل یه معادله درجه دو مینویسیم!اگر دلتاش رو حساب کنیم میبینیم که t توی بازه ای که طولش از 2c بیشتره تغییر میکنه.فکر میکنم که از این بشه نتیجه گرفت که توی این بازه t صحیحی وجود داره که t به پیمانه 2c بشه a.پس x طبیعی و y صحیح میشه.حالا فکر میکنم اگر یکم بیشتر تلاش کنم بتونم کاری کنم که y هم طبیعی شه!:4:
حالا با این حرف ها،این راه حل(حداقل کلیتش) درسته؟!
آخرین ویرایش توسط مدیر
پاسخ : ماراتن نظریه ی اعداد (سطح ممتاز)
به این اتحاد دقت کنید
 (دقت کنید هنوز مسئله حل نشده و ممکنه پرانتز ها منفی بشن.) در واقع الان مسئله رو برای اعداد گویای بین 1/2 و 2 حل کردیم. بقیه اش هم آسونه دیگه. صورت و مخرج رو در مکعب کامل های مناسب ضرب کنین تا بقیه ی اعداد گویا هم ساخته بشن.
(دقت کنید هنوز مسئله حل نشده و ممکنه پرانتز ها منفی بشن.) در واقع الان مسئله رو برای اعداد گویای بین 1/2 و 2 حل کردیم. بقیه اش هم آسونه دیگه. صورت و مخرج رو در مکعب کامل های مناسب ضرب کنین تا بقیه ی اعداد گویا هم ساخته بشن.
سوال بعدی: تمام جواب های گویای دستگاه زیر را بیابید:

لطفاً هر کس حل کرد سوال بعدی رو هم خودش بگذاره.
تایپیک خوبیه که خوابیده تلاش کنید دوباره راش بندازیم هرکی سوالی رو حل کرد سوال بعدی رو بذاره .
سوال 1. ثابت کنید هر عدد گویای مثبت را میتوان به صورت
 نشان داد که
نشان داد که
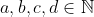
سوال 1. ثابت کنید هر عدد گویای مثبت را میتوان به صورت
سوال بعدی: تمام جواب های گویای دستگاه زیر را بیابید:
لطفاً هر کس حل کرد سوال بعدی رو هم خودش بگذاره.
- ارسال ها
- 6
- لایک ها
- 11
- امتیاز
- 0
پاسخ : ماراتن نظریه ی اعداد (سطح ممتاز)
من یه راه زشت واسش پیدا کردم(اگه جوب نزده باشم!)انقد هم زیاد هست که نمیشه اینجا نوشتش ولی خلاصش اینه که 4 تا متغیر رو به صورت p/q مینویسیم و از روابط عاد کردن نتیجه میشه مخرج ها برابر 1 هستن.اگه کسی دقیق خواست پیام بده واسش عکس میفرستم :4:
بعد که مخرج ها هم یک بشن معلومه که جواب فقط (2و1و0و0)=(d,c,b,a) خواهد بود.(و جایگشتش)
سوال بعد:
این ایده مورد علاقمه:4:
فرض کنید a[SUB]1 [/SUB]= a[SUB]2 [/SUB]= a[SUB]3[/SUB] = 1
a[SUB]n+3[/SUB] = a[SUB]n+2 [/SUB].a[SUB]n+1 +[/SUB] a[SUB]n
[/SUB]ثابت کنید هر عدد طبیعی مانند m مضربی در این دنباله دارد.
سوال بعدی: تمام جواب های گویای دستگاه زیر را بیابید:

لطفاً هر کس حل کرد سوال بعدی رو هم خودش بگذاره.
لطفاً هر کس حل کرد سوال بعدی رو هم خودش بگذاره.
بعد که مخرج ها هم یک بشن معلومه که جواب فقط (2و1و0و0)=(d,c,b,a) خواهد بود.(و جایگشتش)
سوال بعد:
این ایده مورد علاقمه:4:
فرض کنید a[SUB]1 [/SUB]= a[SUB]2 [/SUB]= a[SUB]3[/SUB] = 1
a[SUB]n+3[/SUB] = a[SUB]n+2 [/SUB].a[SUB]n+1 +[/SUB] a[SUB]n
[/SUB]ثابت کنید هر عدد طبیعی مانند m مضربی در این دنباله دارد.
