ماراتن نظریه ی اعداد (سطح ممتاز)
farid_frd گفت
میشه یه مثال بزنین که مربع کامل باشه و p بشماره m رو ولی p^2 نشماره m رو
behrooz1373 گفت
سوال شماره 6)
عدد های صحیح a,b,c,d,k چنان اند که
[center:7bd586ce6c] a^2+k=b^2 و c^2+k=d^2
عدد های صحیح a,b,c,d,k چنان اند که
[center:7bd586ce6c] a^2+k=b^2 و c^2+k=d^2
ثابت کنید عدد 2*(a+b)*(c+d)*(ac+bd-k) مربع کامل است.
کسی سوال 5 رو حل نکرد؟
[/center:7bd586ce6c]
کسی سوال 5 رو حل نکرد؟
[center:7bd586ce6c]
فرض کنید
 عامل اول فردی از
عامل اول فردی از
 هستش. اگر
هستش. اگر
 ، آن گاه
، آن گاه
 و بنابراین میشه از
و بنابراین میشه از
 و
و
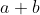 دو تا عامل
دو تا عامل
 فاکتور گرفت که تغییری در مربع کامل بودن عدد ایجاد نمی کنه. با ادامه دادن این روند می تونیم فرض کنیم که هر عامل اول در همزمان در
فاکتور گرفت که تغییری در مربع کامل بودن عدد ایجاد نمی کنه. با ادامه دادن این روند می تونیم فرض کنیم که هر عامل اول در همزمان در
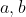 و یا همزمان در
و یا همزمان در
 نیست.
نیست.
حالا دقت کنید که اگر
 اون وقت طبق تساوی بالا، توان در
اون وقت طبق تساوی بالا، توان در
 زوج میشه. ضمن این که
زوج میشه. ضمن این که
 ، چراکه در غیر این صورت مثلا اگر
، چراکه در غیر این صورت مثلا اگر
 اون وقت
اون وقت

حالا دقت کنید که اگر
که تناقضه. پس توان در
 برابر توان
برابر توان
 در
در
 میشه، که گفتیم زوجه.
میشه، که گفتیم زوجه.
در نهایت تنها حالتی که باید بررسی کنیم این حالته که
 . در این حالت اگر
. در این حالت اگر
 آن گاه کافیه ثابت کنیم که
آن گاه کافیه ثابت کنیم که
 زوج میشه (چرا؟). برای این منظور توجه کنید که
زوج میشه (چرا؟). برای این منظور توجه کنید که
 . درنتیجه
. درنتیجه
 [/center:7bd586ce6c][center:7bd586ce6c]
[/center:7bd586ce6c][center:7bd586ce6c]
 و
و
 . عکس این مطلب رو هم به همین ترتیب میشه اثبات کرد یعنی اگر
. عکس این مطلب رو هم به همین ترتیب میشه اثبات کرد یعنی اگر
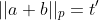 ، آن گاه
، آن گاه
 . بنابراین
. بنابراین
 . یعنی
. یعنی
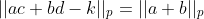 و
و
 .
.
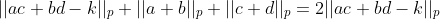
در نهایت تنها حالتی که باید بررسی کنیم این حالته که
حالا نشون میدیم که
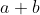 و
و
 نمی تونند همزمان بر بخش پذیر باشند. چراکه در غیر این صورت،
نمی تونند همزمان بر بخش پذیر باشند. چراکه در غیر این صورت،
 [/center:7bd586ce6c]
[/center:7bd586ce6c]
که غیر ممکنه. پس به عنوان مثال
بنابراین
[center:7bd586ce6c]
که همان نتیجه ی مورد نظر است.
در حالت
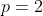 نیز استدلال مشابهی می توان انجام داد.
نیز استدلال مشابهی می توان انجام داد.
[/center:7bd586ce6c]در حالت
M_Sharifi گفت
farid_frd گفت
میشه یه مثال بزنین که مربع کامل باشه و p بشماره m رو ولی p^2 نشماره m رو












