ماراتن هندسه version 2
البته ولی چون که یکی دیگه الان با کامپیوتر کار داره ( از چند ساعت پیش تا حالا هم طول کشیده و احتمالا تا یه چند وقته دیگه هم ادامه داره
) نمی تونم ولی هر وقت کارش تموم بشه راه حالمو می نویسم ... در واقع از این نکته استفاده می کنم که قرینه ی P نسبت به N (مر کز دایره ی نه نقطه) می شه مر کز دایره ای که از H و اون سه تا نقطه می گذره ...
ابتدا یه لمی رو اثبات می کنم:
اگر ABC یک مثلث قائم الزاویه باشه در راس A و O وسط BC باشه و P یک نقطه ی دلخواه روی BA باشه و M یک نقطه ی دلخواه روی صفحه باشه در اون صورت تعریف کنید :
قرینه ی C نسبت به M رو D و قرینه ی A رو نسبت به M هم S بنامید. قرینه ی P نسبت به وسط OD رو K بنامید. از طرفی وسط SD رو L و وسط OD رو Q بنامید. ثابت کنید K روی عمودمنصف SD هست.
هر چند این لم اثباتی هم بدون مختصات دارد ولی من با مختصات حلش می کنم.
مثلث ABC روی روی صفحه ی مختصات به گونه ای قرار دهید که A مبدا مختصات باشد و B روی قسمت مثبت محور y و C روی قسمت مثبت محور x قرار گیرد.
مختصات نقاط را بدین گونه تعریف کنید:
حالا تک تک مختصات نقاط دیگه رو بر حسب همین b,c,x,z,y می شه بدست آورد :
حال بدیهیست که SD موازی محور x هاست. پس عمود منصف آن خطی است با معادله
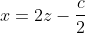و بنابراین کافیست که ثابت شود طول نقطه ی K همین مقدار است.
اما به راحتی بدست می آوریم:
و بدین ترتیب نقطه ی K روی عمود منصف مورد نظر قرار دارد. همانطور که خواست مسئله بود.
حالا کاربرد این لم اینه که در مسئله ی اصلی فرض کنید که وسط BC اسمش M هست و قرینه ی A نسبت به O (
یعنی مرکز دایره ی محیطی) اسمش D هست. از طرفی هم نقطه ی برخورد AP با دایره ی محیطی هم 'A هست. در اون صورت چون AA'D مثلث قائم الزاویه هست اگر لم مسئله رو در نظر بگیریم نتیجه می گیریم که قرینه ی P نسبت به وسط OH یعنی مرکز دایره نه نقطه بر روی عمود منصف ''HA هست که در آن ''A قرینه ی 'A نسبت به M هست. حالا اگر همین موضوع رو برای BP و CP در نظر بگیرید قضیه حله!!
پس قرینه ی P نسبت به مرکز دایره ی نه نقطه میشه مرکز دایره ی ''HA''B''C !!!
حالا خواهشا می شه جواب سوالی روکه کردم بدی ؟
نسبت انعکاس چنده و روی کدوم مثلث و کدوم قاطع قراره منلائوس زده بشه ؟
اگر ABC یک مثلث قائم الزاویه باشه در راس A و O وسط BC باشه و P یک نقطه ی دلخواه روی BA باشه و M یک نقطه ی دلخواه روی صفحه باشه در اون صورت تعریف کنید :
قرینه ی C نسبت به M رو D و قرینه ی A رو نسبت به M هم S بنامید. قرینه ی P نسبت به وسط OD رو K بنامید. از طرفی وسط SD رو L و وسط OD رو Q بنامید. ثابت کنید K روی عمودمنصف SD هست.
هر چند این لم اثباتی هم بدون مختصات دارد ولی من با مختصات حلش می کنم.
مثلث ABC روی روی صفحه ی مختصات به گونه ای قرار دهید که A مبدا مختصات باشد و B روی قسمت مثبت محور y و C روی قسمت مثبت محور x قرار گیرد.
مختصات نقاط را بدین گونه تعریف کنید:
حالا تک تک مختصات نقاط دیگه رو بر حسب همین b,c,x,z,y می شه بدست آورد :
حال بدیهیست که SD موازی محور x هاست. پس عمود منصف آن خطی است با معادله
اما به راحتی بدست می آوریم:
و بدین ترتیب نقطه ی K روی عمود منصف مورد نظر قرار دارد. همانطور که خواست مسئله بود.
حالا کاربرد این لم اینه که در مسئله ی اصلی فرض کنید که وسط BC اسمش M هست و قرینه ی A نسبت به O (
یعنی مرکز دایره ی محیطی) اسمش D هست. از طرفی هم نقطه ی برخورد AP با دایره ی محیطی هم 'A هست. در اون صورت چون AA'D مثلث قائم الزاویه هست اگر لم مسئله رو در نظر بگیریم نتیجه می گیریم که قرینه ی P نسبت به وسط OH یعنی مرکز دایره نه نقطه بر روی عمود منصف ''HA هست که در آن ''A قرینه ی 'A نسبت به M هست. حالا اگر همین موضوع رو برای BP و CP در نظر بگیرید قضیه حله!!
پس قرینه ی P نسبت به مرکز دایره ی نه نقطه میشه مرکز دایره ی ''HA''B''C !!!
حالا خواهشا می شه جواب سوالی روکه کردم بدی ؟
نسبت انعکاس چنده و روی کدوم مثلث و کدوم قاطع قراره منلائوس زده بشه ؟
خوب قبل از این که سراغ اثباتش بریم سعی کنید که با این چیزی که گفتم مسئله ی اصلی رو اثبات کنید ( البته دیگه با این لمی که گفتم مسئله کشکه ... البته راه حل های دیگه ای هم وجود داره که 100% با این راه حل فرق دارند...)
مسئله ی اصلی :
ثابت کنید که وقتی اون نقاط رو نسبت به ضلع قرینه می کنیم مثلثی که به وجود میاد با مثلث 'A'B'C متشابه هست و نقطه ی P به گونه ای هست که در هر دو مثلث نظیر هم هست ( یعنی نقطه ی نظیر P در مثلث 'A'B'C همون P می شه ! )... در حالت خاص ( یعنی همون سوال 1 ) اگر دقت کنید اون دو مثلث متشابه اند و نقطه ی I مرکز ارتفاعی هر دوی آن هاست! یعنی نظیر نقطه ی I در 'A'B'C خودش می شه!)
مسئله ی اصلی :
ثابت کنید که وقتی اون نقاط رو نسبت به ضلع قرینه می کنیم مثلثی که به وجود میاد با مثلث 'A'B'C متشابه هست و نقطه ی P به گونه ای هست که در هر دو مثلث نظیر هم هست ( یعنی نقطه ی نظیر P در مثلث 'A'B'C همون P می شه ! )... در حالت خاص ( یعنی همون سوال 1 ) اگر دقت کنید اون دو مثلث متشابه اند و نقطه ی I مرکز ارتفاعی هر دوی آن هاست! یعنی نظیر نقطه ی I در 'A'B'C خودش می شه!)