- ارسال ها
- 10
- لایک ها
- 3
- امتیاز
- 0
پاسخ : ماراتن هندسه
در واقع باید ثابت کنیم CP زیر میانه ی مثلث ABC است. KL و MN را ادامه می دهیم تا یکدیگر را در D قطع کنند.خط CD ضلع AB را در T قطع میکند.CTt در واقع همان زیرنیانه است. زیرا:
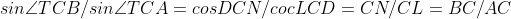
پس کافیست ثابت کنیم خطوط CP و CT بر یکدیگر منطبق اند.
به وضوح KXND محاطی است و همچنین YMLD . ا P نیز بر این دو دایره قرار دارد. فرض کنید خط CD دایره ی محیطی KXN را در P' قطع کند.
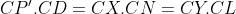
پس P' بر دایره ی محیطی YMCD نیز قرار دارد.
پس P' همان P است.
پس CP همان CT است.
---- دو نوشته به هم متصل شده است ----
اگه درسته اینم سوال بعد: چهارضلعی ABCD مفروض است. نقاط X,Y,Z,T به ترتیب بر نیم خطهای BA,CB,CD,DA قرار دارند به طوریکه:
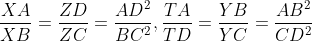
ثابت کنید X,Y,Z,T بر یک دایره یا بر یک خط اند. درضمن ثابت کنید اگر چهارضلعی ABCD محاطی باشد این چهار نقطه بر یک خطند.
در واقع باید ثابت کنیم CP زیر میانه ی مثلث ABC است. KL و MN را ادامه می دهیم تا یکدیگر را در D قطع کنند.خط CD ضلع AB را در T قطع میکند.CTt در واقع همان زیرنیانه است. زیرا:
پس کافیست ثابت کنیم خطوط CP و CT بر یکدیگر منطبق اند.
به وضوح KXND محاطی است و همچنین YMLD . ا P نیز بر این دو دایره قرار دارد. فرض کنید خط CD دایره ی محیطی KXN را در P' قطع کند.
پس P' بر دایره ی محیطی YMCD نیز قرار دارد.
پس P' همان P است.
پس CP همان CT است.
---- دو نوشته به هم متصل شده است ----
اگه درسته اینم سوال بعد: چهارضلعی ABCD مفروض است. نقاط X,Y,Z,T به ترتیب بر نیم خطهای BA,CB,CD,DA قرار دارند به طوریکه:
ثابت کنید X,Y,Z,T بر یک دایره یا بر یک خط اند. درضمن ثابت کنید اگر چهارضلعی ABCD محاطی باشد این چهار نقطه بر یک خطند.
آخرین ویرایش توسط مدیر
