ماراتن هندسه

حمید آنالیز · 1394/1/6

پاسخ : ماراتن هندسه

Dadgarnia گفت

ببخشید من اثبات شما رو متوجه نشدم! الان نقاط روی اضلاع که مرکز دایره ی محاطی مثلثشون بر مرکز دایره ی محاطی مثلث

$ABC$

منطبقه

$D,E,F$

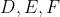هستند؟ اگه اینجوریه چرا

$AD=AE$

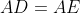هست؟ این اتفاق فقط برای نقطه هایی که دایره ی محاطی بر اضلاع

$AB,AC$

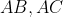در اون نقاط مماسه رخ میده!

---- دو نوشته به هم متصل شده است ----

من سوال بعدو میذارم تا بتونیم ماراتن رو سریع تر پیش ببریم:

$ABCD$

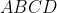یک متوازی الاضلاع است. دایره ی با قطر

$AC$

،

$BD$

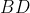را در

$P,Q$

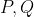قطع می کند. عمودی که از

$C$

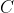بر

$AC$

رسم می شود

$AB,AD$

را به ترتیب در

$X,Y$

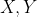قطع می کند. ثابت کنید نقاط

$P,Q,X,Y$

روی یک دایره قرار دارند.

یه سوال اون دایرو مماس قطر هاست؟؟؟!!!!:13:
درون متوازی الاضلاع است یا نه؟!!!:4:

Seyed Amir Hosseini · 1394/1/6

پاسخ : ماراتن هندسه

یعنی دایره ای که مرکزش وسط قطر ad است .

---- دو نوشته به هم متصل شده است ----

یعنی دایره ای که مرکزش وسط قطر AD است .

J.Karimi · 1394/6/1

پاسخ : ماراتن هندسه

با اين كه سوال قبل جواب داده نشده ولي اين سوال رو گفتم اينجا مطرح كنم بهتر باشه تا يه تايپيك ديگه!!!

درمثلث حاده الزاويه

$ABC$

اگر

$CC_{1}$

نيم ساز باشد و O مركز دايره محيطي فرض كنيد محل برخورد ارتفاع نظير راس C و خط

$OC_{1}$

روي دايره محيطي

$AOB$

واقع شود زاويه ي

$ACB$

رابيابيد

Dadgarnia · 1394/6/1

پاسخ : ماراتن هندسه

J.Karimi گفت

محل برخورد این دو خط رو

$C'$

می نامیم. داریم:

$\frac{AC'}{C'B}=\frac{AC_1}{C_1B}=\frac{AC}{CB}$

$AC'^2+BC^2=AC^2+BC'^2$

حالا ثابت می کنیم برای هر چهار عدد حقیقی و مثبت مثل

$a,b,c,d$

که

$\frac{a}{b}=\frac{c}{d},a^2+d^2=c^2+b^2$

داریم

$a=c,b=d$

. داریم:

$(a+d)^2=(b+c)^2\Rightarrow a+d=b+c=s$

$ad=bc=p$

پس این چهار عدد ریشه ی معادله

$x^2-sx+p=0$

هستند پس

$a=c,b=d$

. حالا اگه توی مثلث های

$AKB,ACB$

قضیه کسینوس ها رو بنویسیم بدست میاد:

$a^2+b^2+2ab\cdot \cos 2\angle C=a^2+b^2-2ab\cdot \cos \angle C$

$\Rightarrow 0=\cos \angle C+\cos 2\angle C=(2\cos \angle C-1)(\cos \angle C+1)\Rightarrow \angle C=60^{\circ}$

Sharifi_M · 1394/8/10

پاسخ : ماراتن هندسه

دو دایره با شعاع برابر r، یکی از رئوس A و B و دیگری از رئوس B و C متوازی الاضلاع ABCD میگذرند. M نقطه برخورد دوم این دو دایره است. ثابت کنید شعاع دایره محیطی مثلث AMD برابر است با r.

Dadgarnia · 1394/8/11

پاسخ : ماراتن هندسه

Sharifi_M گفت

مراکز دایره محیطی مثلث های

$ABM,BCM$

رو به ترتیب

$O_1,O_2$

و قرینه ی

$O_1$

نسبت به

$AM$

رو

$O_3$

می نامیم. واضحه که

$O_3A=O_3M=r$

. داریم:

$\angle O_3AB+\angle O_2BA=\angle O_3AM+\angle BAM+\angle ABM+\angle O_2BM$

$=\angle O_1AM+\angle BAM+\angle ABM+\angle O_1BM$

$=\angle O_1MA+\angle BAM+\angle ABM+\angle O_1MB$

$=\angle BMA+\angle BAM+\angle ABM=180$

$\Rightarrow O_3A\parallel O_2B\Rightarrow \angle O_2BC=\angle O_3AD\Rightarrow \overset{\triangle}{O_2BC}\cong \overset{\triangle}{O_3AD}\Rightarrow O_3D=r$

پس

$O_3$

مرکز دایره محیطی مثلث

$AMD$

هست و شعاعش برابره با

$r$

پس حکم ثابت شد.

---- دو نوشته به هم متصل شده است ----

در مثلث

$ABC$

داریم

$AB=AC$

و

$\angle A=20^{\circ}$

. نقاط

$M,N$

به ترتیب روی

$AB,AC$

طوری قرار دارند که

$AM=NC=BC$

ثابت کنید

$\angle BMN=40^{\circ}$

.

assassin1 · 1394/8/11

پاسخ : ماراتن هندسه

سلام صورت سوالو مطمینید مشکلی نداره؟؟؟!!

Sharifi_M · 1394/8/11

پاسخ : ماراتن هندسه

Dadgarnia گفت

من نمیدونم یچنین روش حل یک مساله هندسه درسته یا نه. :/

اگر

$AM=MN$

حکم برقرار میشه.
بعد میشه از حکم برسیم به فرض؟ یعنی فرض کنیم تساوی آخر برقراره و مثلث متساوی الساقینه با بقیه شرط ها بجر اینکه زاویه راس 20 درجست، و از این برسیم به اینکه راس زاویش 20 عه.
اگه این کار درسته دیگه بقیش حله!

Dadgarnia · 1394/8/11

پاسخ : ماراتن هندسه

assassin1 گفت

بله درسته.

---- دو نوشته به هم متصل شده است ----

Sharifi_M گفت

فرض

$AM=MN$

رو نمي توني اضافه كني مگه اينكه يكي از فرض هاي مربوط به

$M,N$

رو حذف كني اونجوري فكر نكنم سوال خيلي فرق كنه.

assassin1 · 1394/8/11

پاسخ : ماراتن هندسه

$\angle BMN$

که منفرجه ست

Dadgarnia · 1394/8/11

پاسخ : ماراتن هندسه

assassin1 گفت

شما شكلتونو اشتباه كشيدين. زاويه بيست درجه خيلي كوچيكه. با جئوجبرا امتحان كنيد درست در مياد.

assassin1 · 1394/8/11

پاسخ : ماراتن هندسه

Dadgarnia گفت

راستش نتونستم راه حلمو بنویسم ولی تو این جور سوالات باید یه سری شکل بسازیم دراین سوال:روی ضلع bcمثلث متساوی الاضلاع bcfرا می سازیم و نقطه fرا به
m,nوصل می کنیم سپس با همیهشتی دو مثلث fcM وaNd و استفاده از اینکه adfb ذوزنقه ی متساوی الساقین است زاویه dبه صورت دو زاویه 20 درجه بدست میاد پس میشه 40 درجه .آیا حل شما هم اینطوره؟!

assassin1 · 1394/8/12

پاسخ : ماراتن هندسه

Dadgarnia گفت

اگه توضیح واضح نیست بگید تا شکلو بکشم

---- دو نوشته به هم متصل شده است ----

سوال:در مثلث متساوی الساقین

$(AB=AC)ABC$

اندازه زاویه

$C$

برابر 80 درجه است.نقطه

$M$

را درون این مثلث چنان انتخاب می کنیم که

$\angle MBA=30,\angle MAB=10$

. مقدار زاویه

$AMC$

را بیابید.

Dadgarnia · 1394/8/12

پاسخ : ماراتن هندسه

assassin1 گفت

$D,E$

چيٓن؟ نه حل من اينجوري نبود.

---- دو نوشته به هم متصل شده است ----

نمي خواين سوالتونو عوض كنيد؟ يه زاويه بازي ساده ست.

assassin1 · 1394/8/12

پاسخ : ماراتن هندسه

ببخشید اصلاح شد. خب راستش سوال ندارم چیکار کنم

Dadgarnia · 1394/8/12

پاسخ : ماراتن هندسه

assassin1 گفت

هنوز هم

$D$

توش هست :| ولي اشكالي نداره من ايده ي شما رو چك كردم و ديدم كه به جواب ميرسه. پس من سوال بعد رو ميذارم:
دو دايره

$\omega_1,\omega_2$

در نقاط

$A,B$

متقاطع اند. خط دلخواهي از

$A$

مي گذرد و

$\omega_1,\omega_2$

را به ترتيب در

$C,D$

(به غير از

$A$

) قطع مي كند. پاي عمود هاي وارد از

$B$

بر مماس هايي كه از نقاط

$C,D$

به ترتيب بر

$\omega_1,\omega_2$

رسم مي شوند را

$E,F$

مي ناميم. ثابت كنيد

$EF$

بر دايره به قطر

$AB$

مماس است.

Sharifi_M · 1394/8/12

پاسخ : ماراتن هندسه

اینم یخورده خیلی آسون نیست؟!
M روی نیمسازه مثلثه و بقیش زاویه بازی و همنهشتی

بعدا نوشت: فکر کردم طراح سوال سوالشو اصلاح کرده :-"

Dadgarnia · 1394/8/12

پاسخ : ماراتن هندسه

Sharifi_M گفت

كدوم سوالو ميگي؟ من سوال جديد گذاشتم.

Sharifi_M · 1394/8/12

پاسخ : ماراتن هندسه

همزمان پست دادیم تقریبا! :4:

REZA 73 · 1394/8/13

پاسخ : ماراتن هندسه

dadgarnia گفت

نقطه تقاطع خط دلخواهی که از

$A$

میگذشت با دایره به قطر

$AB$

را

$K$

فرض کنید. خط

$EF$

در نقطه

$K$

بر دایره مفروض مماس است.
برای ثابت کردن مماسی هم کافی است ثابت کنید چهارضلعی

$KBDF$

و چهارضلعی

$KBCE$

محاطی هستند.

ماراتن هندسه

Well-Known Member

Active Member

Active Member

New Member

New Member

New Member

New Member

New Member

New Member

New Member

New Member

New Member

New Member

New Member

New Member

New Member

New Member

New Member

New Member

Active Member