مسائلی در هندسه مسطحه
پاسخ : مسائلی در هندسه مسطحه
من این سوال رو سه سال پیش دیدم.
این چند تا نکته رو ثابت کنید:
1- دایره ی محیطی
 بر دایره ی محیطی
بر دایره ی محیطی
 مماس است.
مماس است.
2- مماس مشترک این دو دایره از محل برخورد
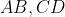 می گذرد.
می گذرد.
3- این محل برخورد رو نقطه ی
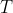 بگیرید.
بگیرید.
4- یکم سینوس و تشابه بنویسید و زاویه بازی هم در صورت لزوم انجام دهید.
این سوال از مجموعه تمرین های بهاری هندسه دبیرستان انرژی اتمیه..احتمالا از سوالای تالیفیه آقای وکیلیه! ..حل نشد...میخواستم بدونم از بچه های انرژی کسی هست که سوالو حل کرده باشه..
نقطه P درون چهار ضلعی محاطی ABCD قرار دارد. و:
BPC =BAP +PDC
E و F و G پای عمود های مرسوم از P به ترتیب بر خطهای AB و AD و DC اند.ثابت کنید مثلث های FEG و PBC متشابه اند

نقطه P درون چهار ضلعی محاطی ABCD قرار دارد. و:
BPC =BAP +PDC
E و F و G پای عمود های مرسوم از P به ترتیب بر خطهای AB و AD و DC اند.ثابت کنید مثلث های FEG و PBC متشابه اند

این چند تا نکته رو ثابت کنید:
1- دایره ی محیطی
2- مماس مشترک این دو دایره از محل برخورد
3- این محل برخورد رو نقطه ی
4- یکم سینوس و تشابه بنویسید و زاویه بازی هم در صورت لزوم انجام دهید.
آخرین ویرایش توسط مدیر
پاسخ : مسائلی در هندسه مسطحه
پاسخ مسئله ی اول) به وضوح مشخص است که دایره محیطی دو مثلث pab و pdc در نقطه ی p بر هم مماسند...( چون bpc=bap + pdc )...

سپس ثابت میکنیم این مماس از محل تلاقی دو ضلع ab و cd میگذرد..
 ودر نهایت از ویژگیهایهای چهار ضلعی های محاطی ایجاد شده ونتایج بدست آمده برای اثبات حکم استفاده میکنیم...
ودر نهایت از ویژگیهایهای چهار ضلعی های محاطی ایجاد شده ونتایج بدست آمده برای اثبات حکم استفاده میکنیم...

پ . ن: با تشکر از کاربر Aref
مسئله ی دو) در مثلث abc بر روی دو ضلع abو ac دو زاویه ی دلخواه را به طور مساوی جدا میکنیم واز b و c بر آنها عمود میکنیم ( f و e)..اگر h پای ارتفاع نظیر راس a و m وسط ضلع bc باشد ثابت کنید e و f و m و h همگی بر روی یک دایره قرار دارند؟؟

پاسخ مسئله ی اول) به وضوح مشخص است که دایره محیطی دو مثلث pab و pdc در نقطه ی p بر هم مماسند...( چون bpc=bap + pdc )...



پ . ن: با تشکر از کاربر Aref
مسئله ی دو) در مثلث abc بر روی دو ضلع abو ac دو زاویه ی دلخواه را به طور مساوی جدا میکنیم واز b و c بر آنها عمود میکنیم ( f و e)..اگر h پای ارتفاع نظیر راس a و m وسط ضلع bc باشد ثابت کنید e و f و m و h همگی بر روی یک دایره قرار دارند؟؟

آخرین ویرایش توسط مدیر
پاسخ : مسائلی در هندسه مسطحه
لم: در یک مثلث، نیمساز خارجی یک زاویه و عمود منصف ضلع روبرو به آن زاویه روی دایره ی محیطی آن مثلث همرسند.

حالا چون چهارضلعی های
 محاطی اند پس
محاطی اند پس
 نیمساز خارجی زاویه ی
نیمساز خارجی زاویه ی
 است.
است.
پس کافیه ثابت کنیم که
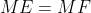 . فرض کنید نقاط
. فرض کنید نقاط
 به ترتیب اوساط اضلاع
به ترتیب اوساط اضلاع
 باشند. در این صورت خیلی راحت میشه دید که
باشند. در این صورت خیلی راحت میشه دید که
 و طبق تساوی اجزای متناظر به دست میاد
و طبق تساوی اجزای متناظر به دست میاد
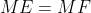 .
.

مسئله ی دو) در مثلث abc بر روی دو ضلع abو ac دو زاویه ی دلخواه را به طور مساوی جدا میکنیم واز b و c بر آنها عمود میکنیم ( f و e)..اگر h پای ارتفاع نظیر راس a و m وسط ضلع bc باشد ثابت کنید e و f و m و h همگی بر روی یک دایره قرار دارند؟؟
حالا چون چهارضلعی های
پس کافیه ثابت کنیم که
- ارسال ها
- 288
- لایک ها
- 344
- امتیاز
- 0
پاسخ : مسائلی در هندسه مسطحه
همون کتاب خوبیه
روی یک مساله شده 1 ساعت هم فکر کن حتی اگه حل هم نکنی ولی چون فکر کردن تو مسائل هندسه مهم ترین عامله مطمئن باش پیشرفت میکنی!
ببخشید میدونم مربوط به تاپیک نیس لطفا پستو حذف نکنید اقا ناظما!
ولی یه سوال داشتم من از کتاب هندسه مسطحه خوشخوان میتونم برای راه انداختن کار مدرسه و قوی شدن هندسه استفاده کنم؟؟؟؟؟یا باید از کتاب سطح پایین تر شروع کنم؟؟؟
مثلا مبتکران 2؟؟؟الگو؟؟
ولی یه سوال داشتم من از کتاب هندسه مسطحه خوشخوان میتونم برای راه انداختن کار مدرسه و قوی شدن هندسه استفاده کنم؟؟؟؟؟یا باید از کتاب سطح پایین تر شروع کنم؟؟؟
مثلا مبتکران 2؟؟؟الگو؟؟
روی یک مساله شده 1 ساعت هم فکر کن حتی اگه حل هم نکنی ولی چون فکر کردن تو مسائل هندسه مهم ترین عامله مطمئن باش پیشرفت میکنی!
پاسخ : مسائلی در هندسه مسطحه
سه محور اصلی این سه دایره یعنی
 هم رس هستند، پس
هم رس هستند، پس
 یک چهار ضلعی کامل می شود که اقطار آن رسم شده اند.پس اگر تقاطع
یک چهار ضلعی کامل می شود که اقطار آن رسم شده اند.پس اگر تقاطع
 و
و
 رو
رو
 بنامیم
بنامیم
=-1) . از اون جایی که
. از اون جایی که
 نیمساز
نیمساز
 هست پس
هست پس
 !
!
سوال سوم) در چهار ضلعی محاطی ABCD محل برخورد دو قطر AC و BD را M مینامیم دوایر محیطی دو مثلث AMD و MBC یکدیگر را برای بار دوم در N قطع میکنند اگر P محل برخورد دو ضلع AB و CD باشند ثابت کنید MN بر PN عمود است؟؟ (هل من مبارز؟؟:196


پاسخ : مسائلی در هندسه مسطحه
بله کاملا درسته.
اینم یه راه حل سطح پایینتر...
راه حل دوم) محل برخورد ارتفاع AN و پاره خط DF رو X مینامیم ثابت میکنیم X همان H محل برخورد ارتفاع هاست..برای این منظور کافیه ثابت کنیم AX*AN= AK*AC (؟)
 با توجه به اینکه پنج نقطه A,D,N,M,F روی یک دایره اند(؟) و تساوی AD و AF میتوان نوشت:
با توجه به اینکه پنج نقطه A,D,N,M,F روی یک دایره اند(؟) و تساوی AD و AF میتوان نوشت:

---- دو نوشته به هم متصل شده است ----
سوال پنجم) این سوال در عین سادگی خیلی جالبه!! در شکل زیر نقاط A,P,Q ثابت اند ..ثابت کنید با تغییر زاویه * پاره خط XY از نقطه ثابتی میگذرد؟!

سوال چهارم نتیجه ی مستقیم قطب و قطبی ه.
اینم یه راه حل سطح پایینتر...
راه حل دوم) محل برخورد ارتفاع AN و پاره خط DF رو X مینامیم ثابت میکنیم X همان H محل برخورد ارتفاع هاست..برای این منظور کافیه ثابت کنیم AX*AN= AK*AC (؟)


---- دو نوشته به هم متصل شده است ----
سوال پنجم) این سوال در عین سادگی خیلی جالبه!! در شکل زیر نقاط A,P,Q ثابت اند ..ثابت کنید با تغییر زاویه * پاره خط XY از نقطه ثابتی میگذرد؟!

آخرین ویرایش توسط مدیر
پاسخ : مسائلی در هندسه مسطحه
سوال هفتم) در شکل زیر دایره محاطی داخلی و محاطی خارجی نظیر راس A در مثلث ABC رسم شده اند..ثابت کنید D'F' , DF , نیمساز A همرسند؟!

---- دو نوشته به هم متصل شده است ----
سوال هشتم) در شکل دو دایره در نقطه ی P مماس داخلند و وتر AB از دایره بزرگتر در نقطه ی N بر دایره کوچکتر مماس است. PN دایره بزرگتر رو در M قطع میکند ( با توجه به اینکه میدونیم M وسط کمان AB است: اینم خودش یه سوال خوبه که میتونید اثبات کنید که البته اینجا سوال ما این نیست!) از M دو مماس MD و ME را بر دایره کوچکتر رسم میکنیم. ثابت کنید چهار نقطه ی A , D , E , B بر روی یک دایره اند؟؟؟

سوال هفتم) در شکل زیر دایره محاطی داخلی و محاطی خارجی نظیر راس A در مثلث ABC رسم شده اند..ثابت کنید D'F' , DF , نیمساز A همرسند؟!

---- دو نوشته به هم متصل شده است ----
سوال هشتم) در شکل دو دایره در نقطه ی P مماس داخلند و وتر AB از دایره بزرگتر در نقطه ی N بر دایره کوچکتر مماس است. PN دایره بزرگتر رو در M قطع میکند ( با توجه به اینکه میدونیم M وسط کمان AB است: اینم خودش یه سوال خوبه که میتونید اثبات کنید که البته اینجا سوال ما این نیست!) از M دو مماس MD و ME را بر دایره کوچکتر رسم میکنیم. ثابت کنید چهار نقطه ی A , D , E , B بر روی یک دایره اند؟؟؟

پاسخ : مسائلی در هندسه مسطحه
راه حل سوال هفتم) ابتدا به لم جالب زیر توجه کنید

محل برخورد DF و نیمساز را M مینامیم از C به M وصل میکنیم و تا C' امتداد میدهیم. طبق لم میدانیم C'C بر AM عمود است و M وسط C'C است..

حال باید ثابت کنیم D'F' نیز از M (وسط C'C ) میگذرد..ابتدا D'F' رارسم میکنیم و سپس C'C را در جهت عمود بر نیمساز خارج میکنیم ( برای اینکار C'CB را به اندازه B/2 - C/2 جدا میکنیم) محل برخورد C'C و D'F' را M مینامیم. کافیست ثابت کنیم M وسط C'C است!!!

( آقا ما این سوالو اصطلاحا با تف حل کردیم..ومیدونم راه حل اصلیش این نیست! اگه کسی راه حلی داره. بگه)
راه حل سوال هفتم) ابتدا به لم جالب زیر توجه کنید



( آقا ما این سوالو اصطلاحا با تف حل کردیم..ومیدونم راه حل اصلیش این نیست! اگه کسی راه حلی داره. بگه)
آخرین ویرایش توسط مدیر
پاسخ : مسائلی در هندسه مسطحه
( آقا ما این سوالو اصطلاحا با تف حل کردیم..ومیدونم راه حل اصلیش این نیست! اگه کسی راه حلی داره. بگه)
برای سوال هفتم می تونید از قطب و قطبی هم استفاده کنید. از b عمود bx و از c عمود cy رو بر نیمساز رسم کنید و ثابت کنید dxd'y محاطیه و بعد نتیجه بگیرید m وسط bc ،مرکز دایره ی محیطی اون هست. بعد نتیجه میشه mx=md پس قوت m نسبت به xو دایره محاطی داخلی برابره. پس m روی محور اصلی اون هاست و روی محور اصلی محاطی داخلی و خارجی هم هست . پس نقطه ی x و دایره محاطی داخلی و خارجی سه تا دایره ی هم محور اند.(نقطه دایره ای به شعاع صفره) از طرفی قطبی های یک نقطه نسبت به یک دسته دایره ی هم محور همرسند. به وضوح سه خطی که مسئله می خواهد ثابت کنیم هم خطند، قطبی های b نسبت به این سه تا دایره اند و اثبات تمامه.
چهار ضلعی های mdpq و mdef محاطی اند. Ef امتداد bc رو در t قطع می کنه. برای اثبات محاطی بودن bpqc کافیه بگیم tp.tq=tb.tc که این هم آسونه. زیرا : Tp.tq=td.tm=te.tf=tb.tc و مسئله حله.
( آقا ما این سوالو اصطلاحا با تف حل کردیم..ومیدونم راه حل اصلیش این نیست! اگه کسی راه حلی داره. بگه)
سوال نهم) در مثلث abc نقاط d,e,f پای اتفاع نظیر رئوس a,b,c هستند. پای عمود وارد از d بر fe را p مینامیم و نقطه q طوری روی fe قرار گرفته که qb=qc ثابت کنید نقاط b,p,q,c هم دایره اند؟!


آخرین ویرایش توسط مدیر
پاسخ : مسائلی در هندسه مسطحه
:97::197:..مرسی فقط این قسمتش چی؟؟ PBQ=PCQ=B-C
سوال دهم) در مثلث متساوی الاضلاع ABC از نقطه دلخواه P بر سه ضلع عمود میکنیم..همچنین از سه راس به P وصل میکنیم..مثلث های ایجاد شده را یکی در میان رنگ میکنیم ثابت کنید مجموع مساحت مثلثهای رنگ شده برابر با مجموع مثلثهای بدون رنگ برابر است؟!

برای سوال هفتم می تونید از قطب و قطبی هم استفاده کنید. از b عمود bx و از c عمود cy رو بر نیمساز رسم کنید و ثابت کنید dxd'y محاطیه و بعد نتیجه بگیرید m وسط bc ،مرکز دایره ی محیطی اون هست. بعد نتیجه میشه mx=md پس قوت m نسبت به xو دایره محاطی داخلی برابره. پس m روی محور اصلی اون هاست و روی محور اصلی محاطی داخلی و خارجی هم هست . پس نقطه ی x و دایره محاطی داخلی و خارجی سه تا دایره ی هم محور اند.(نقطه دایره ای به شعاع صفره) از طرفی قطبی های یک نقطه نسبت به یک دسته دایره ی هم محور همرسند. به وضوح سه خطی که مسئله می خواهد ثابت کنیم هم خطند، قطبی های b نسبت به این سه تا دایره اند و اثبات تمامه.
چهار ضلعی های mdpq و mdef محاطی اند. Ef امتداد bc رو در t قطع می کنه. برای اثبات محاطی بودن bpqc کافیه بگیم tp.tq=tb.tc که این هم آسونه. زیرا : Tp.tq=td.tm=te.tf=tb.tc و مسئله حله.
چهار ضلعی های mdpq و mdef محاطی اند. Ef امتداد bc رو در t قطع می کنه. برای اثبات محاطی بودن bpqc کافیه بگیم tp.tq=tb.tc که این هم آسونه. زیرا : Tp.tq=td.tm=te.tf=tb.tc و مسئله حله.
سوال دهم) در مثلث متساوی الاضلاع ABC از نقطه دلخواه P بر سه ضلع عمود میکنیم..همچنین از سه راس به P وصل میکنیم..مثلث های ایجاد شده را یکی در میان رنگ میکنیم ثابت کنید مجموع مساحت مثلثهای رنگ شده برابر با مجموع مثلثهای بدون رنگ برابر است؟!

آخرین ویرایش توسط مدیر



