معادله ی دیفرانسیل معروف.
پاسخ : معادله ی دیفرانسیل معروف.
بیا سوال رو یه مقدار کامل تر کنیم.
البته نمی دونم در حالت مختلط جواب داره یا نه.
تمام توابع حقیقی و مختلط را بیابید که در رابطه ی
=f(x))
صدق کنند.
تمام توابع حقیقی را بیابید که در رابطه ی
صدق کنند.
یه خواهش:
لینک ندید به جایی، اگر هم میشه دقیق ثابت کنید.
*این هم در نظر داشته باشید که من انتگرال بلد نیستم.
یه خواهش:
لینک ندید به جایی، اگر هم میشه دقیق ثابت کنید.
*این هم در نظر داشته باشید که من انتگرال بلد نیستم.
البته نمی دونم در حالت مختلط جواب داره یا نه.
تمام توابع حقیقی و مختلط را بیابید که در رابطه ی
- ارسال ها
- 1,326
- لایک ها
- 998
- امتیاز
- 113
پاسخ : معادله ی دیفرانسیل معروف.
ببینید یه جورایی حق دارید آقای آرف.آخه به نوعی یک راه برای رسیدن به نپر همین بوده..آقا یه تابع بدید که مشتقش خودش باشه!!
و راهش اینه (از نظر فنی..یعنی ما هنوز نپر نمیدونیم چیه) که یک چند جمله ای با ضرایب دلخواه حدس بزنیم(یعنی فرض کنیم که تابعمان یک چند جمله ای از ایکس هست)بعد جملات هم تا بی نهایته.
بعدش مشتقش مساوی خودش بزاریم.چی میشه؟رابطه بازگشتی بین ضرایب رو میده و an=1/n! s و این ای بتوان ایکسه.بعبارتی کلی ترین تابع رو یافتیم!!
حالا میشه اینو بیایم جورای دیگه هم تعریف کنیم و نشون بدیم هم ارز با نپره.با تعریف اصلی نپر یعنی یک با یک انم بتوان ان وقتی ان میره به بینهایت.
و در ضمن نپر نیست.Napier هست.نا پی یر.ولی همون نپر بگیم مگه مریضیم؟!
ببینید یه جورایی حق دارید آقای آرف.آخه به نوعی یک راه برای رسیدن به نپر همین بوده..آقا یه تابع بدید که مشتقش خودش باشه!!
و راهش اینه (از نظر فنی..یعنی ما هنوز نپر نمیدونیم چیه) که یک چند جمله ای با ضرایب دلخواه حدس بزنیم(یعنی فرض کنیم که تابعمان یک چند جمله ای از ایکس هست)بعد جملات هم تا بی نهایته.
بعدش مشتقش مساوی خودش بزاریم.چی میشه؟رابطه بازگشتی بین ضرایب رو میده و an=1/n! s و این ای بتوان ایکسه.بعبارتی کلی ترین تابع رو یافتیم!!
حالا میشه اینو بیایم جورای دیگه هم تعریف کنیم و نشون بدیم هم ارز با نپره.با تعریف اصلی نپر یعنی یک با یک انم بتوان ان وقتی ان میره به بینهایت.
و در ضمن نپر نیست.Napier هست.نا پی یر.ولی همون نپر بگیم مگه مریضیم؟!
پاسخ : معادله ی دیفرانسیل معروف.
دو روش برای اثبات مشتق lnu وجود داره.یکی قاعده زنجیره ای و دیگری هم استفاده از این نکته که مشتق lnx میشه 1/x .دومی خیلی قشنگه اما الان بهش نمی پردازیم.
اول از همه داریم.
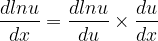
من توی سه چهار تا کتاب مختلف رفتم اثبات مشتق lnx رو نگاه کردم تقریبا همه شون فرض کرده بودند که مشتق lnx میشه 1/x و من واقعا اثباتی ندیدم!!!اگه کسی توضیحی داره در این رابطه ممنون میشم بگه.
حالا داریم!
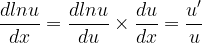
دو روش برای اثبات مشتق lnu وجود داره.یکی قاعده زنجیره ای و دیگری هم استفاده از این نکته که مشتق lnx میشه 1/x .دومی خیلی قشنگه اما الان بهش نمی پردازیم.
اول از همه داریم.
من توی سه چهار تا کتاب مختلف رفتم اثبات مشتق lnx رو نگاه کردم تقریبا همه شون فرض کرده بودند که مشتق lnx میشه 1/x و من واقعا اثباتی ندیدم!!!اگه کسی توضیحی داره در این رابطه ممنون میشم بگه.
حالا داریم!
- ارسال ها
- 1,326
- لایک ها
- 998
- امتیاز
- 113
پاسخ : معادله ی دیفرانسیل معروف.
گفتم که ....نپر ..یعنی تابع اکسپتانسیل تعریف شده.بعدن اومدن براش تابع معکوسی تعریف کردن.دیدن خاصیت لگاریتمی داره و...
دیگه چی شد؟شد لگاریتم تو مبنای e.
و یک نکته هم بگم..اساسن مشتق توابع نمایی و لگاریتمی از اینجا شروع شد که تابع اکسپوتانسیل (که تو اون معادله صدق میکنه) هم ارز با یک عددی بتوان x نشان داده شد.و طبق معادله دبفرانسیلی که براش داشتن دیدن که این تابع معکوسش تو این باید صدق کنه.پس ln و مشتق ln بوجود آمد...
و خداوند ln را آفرید!!
البته من تاریخچه شو یکم پیچوندم چون دقیقن این نبود..هم زمان داشته کارهای مختلفی تو زمینه های مختلفی انجام میشده که بهم گره خورده...
برنولی عدد e رو بهش تو محاسبه سود بانک خورد و اون تعریف معروف یک بعلاوه یک ایکسم و.. رو درآورد از طرفی اویلر هم تو یه زمینه دیگه به این خورد و..!!
دو روش برای اثبات مشتق lnu وجود داره.یکی قاعده زنجیره ای و دیگری هم استفاده از این نکته که مشتق lnx میشه 1/x .دومی خیلی قشنگه اما الان بهش نمی پردازیم.
اول از همه داریم.
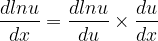
من توی سه چهار تا کتاب مختلف رفتم اثبات مشتق lnx رو نگاه کردم تقریبا همه شون فرض کرده بودند که مشتق lnx میشه 1/x و من واقعا اثباتی ندیدم!!!اگه کسی توضیحی داره در این رابطه ممنون میشم بگه.
حالا داریم!
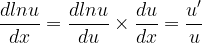
اول از همه داریم.
من توی سه چهار تا کتاب مختلف رفتم اثبات مشتق lnx رو نگاه کردم تقریبا همه شون فرض کرده بودند که مشتق lnx میشه 1/x و من واقعا اثباتی ندیدم!!!اگه کسی توضیحی داره در این رابطه ممنون میشم بگه.
حالا داریم!
دیگه چی شد؟شد لگاریتم تو مبنای e.
و یک نکته هم بگم..اساسن مشتق توابع نمایی و لگاریتمی از اینجا شروع شد که تابع اکسپوتانسیل (که تو اون معادله صدق میکنه) هم ارز با یک عددی بتوان x نشان داده شد.و طبق معادله دبفرانسیلی که براش داشتن دیدن که این تابع معکوسش تو این باید صدق کنه.پس ln و مشتق ln بوجود آمد...
و خداوند ln را آفرید!!
البته من تاریخچه شو یکم پیچوندم چون دقیقن این نبود..هم زمان داشته کارهای مختلفی تو زمینه های مختلفی انجام میشده که بهم گره خورده...
برنولی عدد e رو بهش تو محاسبه سود بانک خورد و اون تعریف معروف یک بعلاوه یک ایکسم و.. رو درآورد از طرفی اویلر هم تو یه زمینه دیگه به این خورد و..!!
پاسخ : معادله ی دیفرانسیل معروف.
عارف جان.
تا اونجا که من فهمیدم و ایمان هم اشاره کرد تعریف می کنیم که مشتق lnx میشه 1/x .اصلا توی بعضی کتابا واقعا شاخ در میاوردم میدیدم چطور این رو اثبات کردند:152:!! در واقع اثباتی در کار نیست!!فقط یه توجیهه!
حالا نیازی هم به کمک گرفتن از بسط e^x نیست.
کارهای زیر رو هم میشه انجام داد که مشتق e^x رو بدست بیاریم.
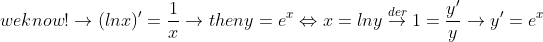
منم دیشب به این رسیدم که باید ثابت کنیم:
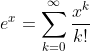
تا اونجا که من فهمیدم و ایمان هم اشاره کرد تعریف می کنیم که مشتق lnx میشه 1/x .اصلا توی بعضی کتابا واقعا شاخ در میاوردم میدیدم چطور این رو اثبات کردند:152:!! در واقع اثباتی در کار نیست!!فقط یه توجیهه!
حالا نیازی هم به کمک گرفتن از بسط e^x نیست.
کارهای زیر رو هم میشه انجام داد که مشتق e^x رو بدست بیاریم.
پاسخ : معادله ی دیفرانسیل معروف.
در نظر داشته باشید که من اندازه ی حسابان سوم بلدم. چرا اینو داریم؟
اگه میشه همه چیو از اون تعریف سود بانکی توی بی نهایت روز ثابت کنید.
^n)
عارف جان.
تا اونجا که من فهمیدم و ایمان هم اشاره کرد تعریف می کنیم که مشتق lnx میشه 1/x .اصلا توی بعضی کتابا واقعا شاخ در میاوردم میدیدم چطور این رو اثبات کردند:152:!! در واقع اثباتی در کار نیست!!فقط یه توجیهه!
حالا نیازی هم به کمک گرفتن از بسط e^x نیست.
کارهای زیر رو هم میشه انجام داد که مشتق e^x رو بدست بیاریم.
'=\frac{1}{x}\rightarrow theny=e^x\Leftrightarrow x=lny\overset{der}{\rightarrow}1=\frac{y'}{y}\rightarrow y'=e^x)
تا اونجا که من فهمیدم و ایمان هم اشاره کرد تعریف می کنیم که مشتق lnx میشه 1/x .اصلا توی بعضی کتابا واقعا شاخ در میاوردم میدیدم چطور این رو اثبات کردند:152:!! در واقع اثباتی در کار نیست!!فقط یه توجیهه!
حالا نیازی هم به کمک گرفتن از بسط e^x نیست.
کارهای زیر رو هم میشه انجام داد که مشتق e^x رو بدست بیاریم.
اگه میشه همه چیو از اون تعریف سود بانکی توی بی نهایت روز ثابت کنید.
- ارسال ها
- 1,326
- لایک ها
- 998
- امتیاز
- 113
پاسخ : معادله ی دیفرانسیل معروف.
!!! ما هم دنبال کاملترین تابع تحلیلی هستیم که تو اون معادله صدق میکنه.
میرسیم به تابع نمایی e .
و برای نشون دادن هم ارزی اون ..با توجه به تعریف برنولی بسادگی میبینیم جمله ها برابرند پس تابع ما نپر بتوان ایکسه.
بعدش هم میایم معکوس تابع رو تعریف میکنیم (یعنی لگاریتم اصلن از اینجا و توسط ناپیر اختراع شد) و از تعریف نپر میرسیم به ln و مشتقش.
و اما برای یک تابع غیر تحلیلی....ما اینجا دقیقن نگفتیم تابعمون تحلیلیه.فقط فرض کردیم میشه حول 0 بشکل یک چندجمله ای بسطش داد...یعنی حول 0 خوشرفتاره..همین.
و تابع غیر تحلیلی اصلن بدردمون زیاد نمیخوره.
اصلن برای پیدا کردن توابع تحلیلی خیلی کوشش شده توسط وایراستراوس چون کار راحتی نیست...و بعدن تابعی کشف کرد که همه جا تحلیلی و روونه(continous) ولی هیچ حا مشتق پذیر نیست!!
و ما اینجا کلن دنبال توابع غیر تحلیلی نیستیم.اصلن تو معادله دیفرانسیل مشتقش هست!!بیخیال غیر تحلیلی میشیم.
!!! ما هم دنبال کاملترین تابع تحلیلی هستیم که تو اون معادله صدق میکنه.
میرسیم به تابع نمایی e .
و برای نشون دادن هم ارزی اون ..با توجه به تعریف برنولی بسادگی میبینیم جمله ها برابرند پس تابع ما نپر بتوان ایکسه.
بعدش هم میایم معکوس تابع رو تعریف میکنیم (یعنی لگاریتم اصلن از اینجا و توسط ناپیر اختراع شد) و از تعریف نپر میرسیم به ln و مشتقش.
و اما برای یک تابع غیر تحلیلی....ما اینجا دقیقن نگفتیم تابعمون تحلیلیه.فقط فرض کردیم میشه حول 0 بشکل یک چندجمله ای بسطش داد...یعنی حول 0 خوشرفتاره..همین.
و تابع غیر تحلیلی اصلن بدردمون زیاد نمیخوره.
اصلن برای پیدا کردن توابع تحلیلی خیلی کوشش شده توسط وایراستراوس چون کار راحتی نیست...و بعدن تابعی کشف کرد که همه جا تحلیلی و روونه(continous) ولی هیچ حا مشتق پذیر نیست!!
و ما اینجا کلن دنبال توابع غیر تحلیلی نیستیم.اصلن تو معادله دیفرانسیل مشتقش هست!!بیخیال غیر تحلیلی میشیم.
پاسخ : معادله ی دیفرانسیل معروف.
توی یکی از پستام من این رو با روش معروف خودم حل کردم!!
با کمک این پست راحت می تونید اثباتش کنید.
مراحل هم عین هم هستند.
------------------------------------------------------------------------------------
حالا روشم رو میذارم.
راه سوم جناب torna تقریبا شبیه به اینیه که می خوام بنویسم اما خیلی جمع و جور تر و تر و تمیز تر.
اولین باری که از این روش استفاده کردم توی حد
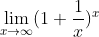بود و قبلا جای دیگه ای ندیدم از این روش استفاده بشه. این روشی که می خوام بنویسم کاربرد خیلی گسترده ای توی حد های بی نهایت داره.نه تنها حد هایی که دامنه شون اعداد حقیقیه.بلکه بعضی از حد هایی که دامنه شون اعداد طبیعیه هم میشه از این روش استفاده کرد.مثلا تابع رو به توان x می رسونیم و کار های زیر رو انجام میدیم و در نهایت به جای x یک میذاریم.حالا اینجا دامنه اعداد حقیقیه و کارمون سبکتره.
اول یه قضیه رو بیان می کنم و میرم سراغ حل سوال.
قضیه.اگر تابعی با دامنه اعداد حقیقی و مشتقپذیر در دامنه ش داشته باشیم آنگاه این تابع در بی نهایت تمامی رفتارهای مجانب رو به خودش میگیره که یکی از اونها برابر شدن مشتق تابع و مجانبه که داریم. (اگه مجانب افقی باشه)
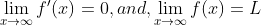اثبات اون قسمت صفر شدن مشتق هم به نظر خودم با برهان خلف میشه انجام داد!
اول با فرض همگرا بودن تابع مورد سوال پیش میریم اگه تابع همگرا نبود آخرای کار یه گیرایی پیش میاد.اگه به مشکلی برنخوریم تابع همگراست و نیازی به اثباتای خفن نداره و از روش میگذریم.
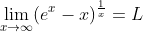
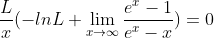
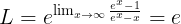
شاید توی این سوال راه خوبی نباشه راه من اما کاربردش خیلی زیاده و جاهایی که خیلی گیر می کنیم اون قضیه ای که نوشتم وحشتناک راهگشاست.همون طور که گفتم میشه روی اعداد طبیعی هم اجراش کرد که از مزیت هاشه!!
در نظر داشته باشید که من اندازه ی حسابان سوم بلدم. چرا اینو داریم؟
اگه میشه همه چیو از اون تعریف سود بانکی توی بی نهایت روز ثابت کنید.
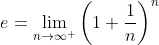
اگه میشه همه چیو از اون تعریف سود بانکی توی بی نهایت روز ثابت کنید.
با کمک این پست راحت می تونید اثباتش کنید.
مراحل هم عین هم هستند.
------------------------------------------------------------------------------------
حالا روشم رو میذارم.
راه سوم جناب torna تقریبا شبیه به اینیه که می خوام بنویسم اما خیلی جمع و جور تر و تر و تمیز تر.
اولین باری که از این روش استفاده کردم توی حد
اول یه قضیه رو بیان می کنم و میرم سراغ حل سوال.
قضیه.اگر تابعی با دامنه اعداد حقیقی و مشتقپذیر در دامنه ش داشته باشیم آنگاه این تابع در بی نهایت تمامی رفتارهای مجانب رو به خودش میگیره که یکی از اونها برابر شدن مشتق تابع و مجانبه که داریم. (اگه مجانب افقی باشه)
اول با فرض همگرا بودن تابع مورد سوال پیش میریم اگه تابع همگرا نبود آخرای کار یه گیرایی پیش میاد.اگه به مشکلی برنخوریم تابع همگراست و نیازی به اثباتای خفن نداره و از روش میگذریم.
پس یا L=0 یا پرانتز صفره.اگه L=0 باشه به کمک نا مساوی رشد خیلی راحت ردش می کنیم.
پس داریم
پس داریم
شاید توی این سوال راه خوبی نباشه راه من اما کاربردش خیلی زیاده و جاهایی که خیلی گیر می کنیم اون قضیه ای که نوشتم وحشتناک راهگشاست.همون طور که گفتم میشه روی اعداد طبیعی هم اجراش کرد که از مزیت هاشه!!
- ارسال ها
- 1,326
- لایک ها
- 998
- امتیاز
- 113
پاسخ : معادله ی دیفرانسیل معروف.
این چیزی که هست اولین تعریف نپره!!اصلن عدد نپر چیه؟؟میگیم اینه!!
حالا شما اگر میخواید باید نشان دهید اینو میشه بشکل یک ای بتوان ایکس نوشت و اون ای رو بدست آورید.نه اینکه بگید e هست دیگه!!!e کیه!؟e رو باید در بیاریم.
و اینکه این روش شما...میخواستیم از چی به چی برسیم؟!
یعنی ما دقیقن چی رو ثابت کردیم؟؟
سود بانکی رو رسیدن بهش راهته...راحت میشه ریسد به تعریف برنولی بقیش یکم سخت میشه.
و ضمن اینکه الان میخواستیم اینو بگیرم بسطشم مینوشتیم واضح بود.
توی یکی از پستام من این رو با روش معروف خودم حل کردم!!
با کمک این پست راحت می تونید اثباتش کنید.
مراحل هم عین هم هستند.
------------------------------------------------------------------------------------
حالا روشم رو میذارم.
راه سوم جناب torna تقریبا شبیه به اینیه که می خوام بنویسم اما خیلی جمع و جور تر و تر و تمیز تر.
اولین باری که از این روش استفاده کردم توی حد
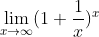بود و قبلا جای دیگه ای ندیدم از این روش استفاده بشه. این روشی که می خوام بنویسم کاربرد خیلی گسترده ای توی حد های بی نهایت داره.نه تنها حد هایی که دامنه شون اعداد حقیقیه.بلکه بعضی از حد هایی که دامنه شون اعداد طبیعیه هم میشه از این روش استفاده کرد.مثلا تابع رو به توان x می رسونیم و کار های زیر رو انجام میدیم و در نهایت به جای x یک میذاریم.حالا اینجا دامنه اعداد حقیقیه و کارمون سبکتره.
اول یه قضیه رو بیان می کنم و میرم سراغ حل سوال.
قضیه.اگر تابعی با دامنه اعداد حقیقی و مشتقپذیر در دامنه ش داشته باشیم آنگاه این تابع در بی نهایت تمامی رفتارهای مجانب رو به خودش میگیره که یکی از اونها برابر شدن مشتق تابع و مجانبه که داریم. (اگه مجانب افقی باشه)
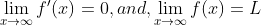اثبات اون قسمت صفر شدن مشتق هم به نظر خودم با برهان خلف میشه انجام داد!
اول با فرض همگرا بودن تابع مورد سوال پیش میریم اگه تابع همگرا نبود آخرای کار یه گیرایی پیش میاد.اگه به مشکلی برنخوریم تابع همگراست و نیازی به اثباتای خفن نداره و از روش میگذریم.
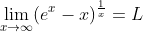
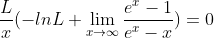
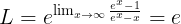
شاید توی این سوال راه خوبی نباشه راه من اما کاربردش خیلی زیاده و جاهایی که خیلی گیر می کنیم اون قضیه ای که نوشتم وحشتناک راهگشاست.همون طور که گفتم میشه روی اعداد طبیعی هم اجراش کرد که از مزیت هاشه!!
با کمک این پست راحت می تونید اثباتش کنید.
مراحل هم عین هم هستند.
------------------------------------------------------------------------------------
حالا روشم رو میذارم.
راه سوم جناب torna تقریبا شبیه به اینیه که می خوام بنویسم اما خیلی جمع و جور تر و تر و تمیز تر.
اولین باری که از این روش استفاده کردم توی حد
اول یه قضیه رو بیان می کنم و میرم سراغ حل سوال.
قضیه.اگر تابعی با دامنه اعداد حقیقی و مشتقپذیر در دامنه ش داشته باشیم آنگاه این تابع در بی نهایت تمامی رفتارهای مجانب رو به خودش میگیره که یکی از اونها برابر شدن مشتق تابع و مجانبه که داریم. (اگه مجانب افقی باشه)
اول با فرض همگرا بودن تابع مورد سوال پیش میریم اگه تابع همگرا نبود آخرای کار یه گیرایی پیش میاد.اگه به مشکلی برنخوریم تابع همگراست و نیازی به اثباتای خفن نداره و از روش میگذریم.
پس یا L=0 یا پرانتز صفره.اگه L=0 باشه به کمک نا مساوی رشد خیلی راحت ردش می کنیم.
پس داریم
پس داریم
شاید توی این سوال راه خوبی نباشه راه من اما کاربردش خیلی زیاده و جاهایی که خیلی گیر می کنیم اون قضیه ای که نوشتم وحشتناک راهگشاست.همون طور که گفتم میشه روی اعداد طبیعی هم اجراش کرد که از مزیت هاشه!!
حالا شما اگر میخواید باید نشان دهید اینو میشه بشکل یک ای بتوان ایکس نوشت و اون ای رو بدست آورید.نه اینکه بگید e هست دیگه!!!e کیه!؟e رو باید در بیاریم.
و اینکه این روش شما...میخواستیم از چی به چی برسیم؟!
یعنی ما دقیقن چی رو ثابت کردیم؟؟
سود بانکی رو رسیدن بهش راهته...راحت میشه ریسد به تعریف برنولی بقیش یکم سخت میشه.
و ضمن اینکه الان میخواستیم اینو بگیرم بسطشم مینوشتیم واضح بود.
پاسخ : معادله ی دیفرانسیل معروف.
ریاضیات اینقدر هم نامنظم نیست که هرچیزی بی دلیل باشه !! :68:
برای اثبات مشتق lnX یه راهش استفاده از تعریف حدی e هستش :
روش بعدیش اینه که تابع lnX رو به صورت یه انتگرال تعریف میکنن و ثابت میکنند خواص لگاریتم رو داره و .... ! بعدش برای مشتقش هم از قضیه اساسی حساب استفاده میشه :
و بقیه روشها رو هنوز نمیدونم !!
ریاضیات اینقدر هم نامنظم نیست که هرچیزی بی دلیل باشه !! :68:
برای اثبات مشتق lnX یه راهش استفاده از تعریف حدی e هستش :
روش بعدیش اینه که تابع lnX رو به صورت یه انتگرال تعریف میکنن و ثابت میکنند خواص لگاریتم رو داره و .... ! بعدش برای مشتقش هم از قضیه اساسی حساب استفاده میشه :
و بقیه روشها رو هنوز نمیدونم !!
