نابرابری برای ب.م.م
vvvvvvvvvvvaaaaaaaaaayyyyyyyyyyyy
پوزش می طلبم


 اصلا معلوم نیست دارم چی کار می کنم !!! منو ببخشید !!! ...
اصلا معلوم نیست دارم چی کار می کنم !!! منو ببخشید !!! ...
در واقع پیش خودم این طوری فکر کردم که ...

قرار دهید :
 و هم چنین
و هم چنین
 حالا کافیه ثابت کنیم که به ازای n های به اندازه ی کافی بزرگ داریم :
حالا کافیه ثابت کنیم که به ازای n های به اندازه ی کافی بزرگ داریم :
 (چرا ؟) و این یعنی این که
(چرا ؟) و این یعنی این که
 در ادامه داریم :
در ادامه داریم :
 پس به دست می آوریم :
پس به دست می آوریم :
 .... عجب سوتی گنده ای نه
.... عجب سوتی گنده ای نه

 ... و این یعنی
... و این یعنی
 ... به خاطر همین بود که گفتم به جای 4 می شه هر عدد حقیقی رو گذاشت !!!
... به خاطر همین بود که گفتم به جای 4 می شه هر عدد حقیقی رو گذاشت !!!
باز هم معذرت می خوام ...
حالا هم که شما ایده ی حل سوال رو گفتید ... پس مسئله سوخت

پوزش می طلبم



در واقع پیش خودم این طوری فکر کردم که ...

قرار دهید :









باز هم معذرت می خوام ...
حالا هم که شما ایده ی حل سوال رو گفتید ... پس مسئله سوخت

مجموع
 برابر است با
برابر است با
 به علاوه ی دو برابر مجموع ب.م.م های به فرم
به علاوه ی دو برابر مجموع ب.م.م های به فرم
 ، که
، که
 و
و
 و
و
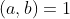 . اگر
. اگر
 را ثابت در نظر بگیریم، آن گاه
را ثابت در نظر بگیریم، آن گاه
 . بنابراین مجموع همه ی این ب.م.م ها برابر است با
. بنابراین مجموع همه ی این ب.م.م ها برابر است با
[center:29401aea16]

[center:29401aea16]
از طرفی

در نتیجه


از طرفی
که مجموع بالا روی همه ی اعداد اول کوچک تر از
 محاسبه شده است. حال اگر
محاسبه شده است. حال اگر
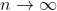 ، مجموع واگرا می شود. بنابراین برای هر
، مجموع واگرا می شود. بنابراین برای هر
 ، نابرابری
، نابرابری
 برای
برای
 های به اندازه ی کافی بزرگ برقرار است.
های به اندازه ی کافی بزرگ برقرار است.
[/center:29401aea16]

