- ارسال ها
- 350
- لایک ها
- 683
- امتیاز
- 93
سلام دوستان گرامی،
اولین مسابقهی فیتیلستان ریاضی از امروز آغاز شده و تا صبح جمعهی هفتهی آینده (23 آبان) ادامه دارد. برای آشنایی با مسابقه و جوایز آن به اینجا بروید.
در این دور از مسابقه هر کاربر فقط یک بار میتواند پاسخ سوال داده شده را در ادامهی تاپیک بنویسد و در پایان 10 مسابقه، همهی جوابها به همراه امتیازهای تعلق گرفته به آنها منتشر خواهد شد. فقط 11 هفتهی دیگر، برندگان سری اول فیتیلستان ریاضی معرفی میشوند و جوایز ایشان اهدا خواهد شد.
[HR][/HR]سوال فیتیلستان 1 ریاضی
بخش اول (نظریهی اعداد)
جایگشت
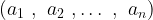 از اعداد
از اعداد
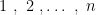 را مربعی مینامیم هرگاه حداقل یکی از اعداد
را مربعی مینامیم هرگاه حداقل یکی از اعداد

مربع کامل باشند. بزرگترین عدد
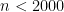 را بیابید که هریک از جایگشتهای
را بیابید که هریک از جایگشتهای
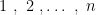 مربعی باشند.
مربعی باشند.
بخش دوم (جبر)
آیا عدد طبیعی
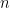 وجود دارد که بتوان مجموعهی
وجود دارد که بتوان مجموعهی
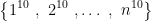 را به ده زیرمجموعه با مجموع اعضای یکسان افراز کرد؟
را به ده زیرمجموعه با مجموع اعضای یکسان افراز کرد؟
اولین مسابقهی فیتیلستان ریاضی از امروز آغاز شده و تا صبح جمعهی هفتهی آینده (23 آبان) ادامه دارد. برای آشنایی با مسابقه و جوایز آن به اینجا بروید.
در این دور از مسابقه هر کاربر فقط یک بار میتواند پاسخ سوال داده شده را در ادامهی تاپیک بنویسد و در پایان 10 مسابقه، همهی جوابها به همراه امتیازهای تعلق گرفته به آنها منتشر خواهد شد. فقط 11 هفتهی دیگر، برندگان سری اول فیتیلستان ریاضی معرفی میشوند و جوایز ایشان اهدا خواهد شد.
[HR][/HR]سوال فیتیلستان 1 ریاضی
بخش اول (نظریهی اعداد)
جایگشت
-=-=-=-=-=-=-=--=-=-=-=-=-=-=-=-=-=-=-=-=--=-=-=-=-=-=-=-=-=-=-=-=-=--=-=-=-=-=-=-=-=-=-=-=-=-=--=-=-=-=-=-=-=-=-=-=-=-=-=--=-
بخش دوم (جبر)
آیا عدد طبیعی
طراح سوالات این مسابقه: محمد شریفی
[HR][/HR]بهتر است با دلایل کافی، توضیح هر بخش را بنویسید و در صورت نیاز به محاسبه، آن را نیز همینجا وارد کنید. دو بخش فرمول نویس (Fx در ادیتور) و آپلودسنتر آیریسک برای گویا و زیبا نوشتن پاسخها به شما کمک خواهند کرد.
